Keywords
|
| OFDM, ACE Algorithm, SNR, BER |
INTRODUCTION
|
| Orthogonal Frequency Division Multiplexing (OFDM) is a method of Digital Modulation in which a signal is split into several narrowband channels at different frequencies. The OFDM technology was first conceived in the 1960s and 1970s during the research into minimizing interference among the channels near each other in frequency [1]. The OFDM divides the frequency spectrum into sub-bands small enough so that the channel effects are constant (flat) over a given sub-band. Then a classical IQ modulation (BPSK, QPSK, MQAM, etc) is sent over the sub-band. If designed correctly, all the fast changing effects of the channel disappear as they are now occurring during the transmission of a single symbol and are thus treated as flat fading at the received [2]. Orthogonal Frequency Division Multiplexing (OFDM) is a promising technique for achieving high data rate and combating multipath fading in Wireless Communications. OFDM can be thought of as a hybrid of Multi Carrier Modulation (MCM) and Frequency Shift Keying (FSK) modulation [3]. |
| Orthogonal Frequency Division Multiplexing (OFDM) is a multiplexing technique that became more popular in the recent years due to the development of Digital Signal Processors (DSPs) that can handle its heavy digital processing requirements [4]. Orthogonal Frequency Division Multiplexing (OFDM) system is a Multi-Carrier Modulation (MCM) scheme in which many parallel data streams are transmitted at the same time over a channel, with each transmitting only a small part of the total data rate. With OFDM, a high-speed digital message is divided into a large number of separate carrier waves [5]. The receiving system reconstructs the message from the separate carriers. The technique is a coding and transport scheme comparable to the way that Code Division Multiple Access (CDMA) is a coding scheme [6].The problem of overhead carrier spacing required in Frequency Division Multiple Access (FDMA) can be recovered. |
| The Orthogonal Frequency Division Multiplexing (OFDM) systems has been popularly developed for the Wideband Digital Communication Systems, whether wireless or over copper wires, used in the applications such as Digital Television (D-TV), Digital Audio Broadcasting (DAB), Digital Video Broadcasting (DVB), Broadband Internet Access and Wireless Networking [7]. The key idea of the Exponential Companding Transform is to effectively reduce the Peak-to-Average Power Ratio (PAPR) of the transmitted or the companded [8]. The process of companding enlarges the amplitudes of the small signals, while the peaks remain unchanged. Therefore, the average power is increased and thus the Peak-to-Average Power Ratio (PAPR) can be reduced [9]. |
RELATED WORK
|
| In this paper a new phase sequence is generated, and is carried out by first generating the matrix of phase sequence and then partitioning it based on the requirement for PAPR reduction and complexity. With this new phase sequence the complexity of PTS reduces significantly as it reduces the number of IFFT, at the expense of a slight PAPR degradation. There are several papers that study the effects of the nonlinear PA in OFDM systems [10], [11]. The proposed PTS scheme is examined by simulation, considering the effects of Saleh model PA [12]. To enhance the efficiency and linearity of the PA, digital predistortion (DPD) [11], [13] is added to the system. The effects of the Saleh model power amplifier are examined with proposed PTS and DPD. The combination of the proposed PTS and DPD have significant reduction in power consumption and increase in power efficiency and can be applied in modern wireless communication device. |
| PAPR is a random variable because it is a function of the input data, and the input data are random variable. Therefore PAPR can be calculated by using level crossing rate theorem that calculates the average number of times that the envelope of a signal crosses a given level. Knowing the amplitude distribution of the OFDM output signals, it is easy to compute the probability that the instantaneous amplitude will be above a given threshold and the same goes for power. It should be noted that all the elements of each row of matrix b are of the same values and this is in accordance with the C-PTS method. It should be noted that in order to have exact PAPR calculation, at least 4 times oversampling is necessary. As the oversampling of x, add zeros to the vector, hence the number of phase sequence to multiply to matrix x will remain the same. |
| The Exponential Companding Transform can effectively reduce the PAPR of transmitted i.e., companded OFDM signals by transforming the statistics of the amplitudes of these signals into uniform distribution. The new scheme also has the advantage of maintaining a constant average power level in the nonlinear companding operation. The companding transform maintains the same average power level as that of the original OFDM signals and can also adjust the amplitudes of both large and small input signals, while maintaining the average power unchanged by properly choosing the transform parameters, so as to make the output signals have an uniform distribution. |
| The Nonlinear Companding Transform is the most attractive scheme due to its good system performance and simplicity, also effectively reduces Peak-to-Average Power Ratio (PAPR) for different modulation formats and subcarrier sizes without any complexity increase and bandwidth expansion. An important task in the design of future OFDM system is to exploit frequency selective channels by adaptable transmission parameters (bandwidth, coding/data rate, power) to preserve power and bandwidth efficiency according to channel conditions at the receiver. The SNR is defined as the ratio of the desired signal power to the noise power and is widely used as a standard measure of signal quality for communication systems. SNR estimators derive estimate by averaging the observable properties of the received signal over a number of symbols. Prior to SNR per subcarrier estimation for adaptive transmission, the average SNR and channel frequency response have to be estimated. |
| This paper addresses the sub block phase weighting (SPW) method to reduce the peak-to-average power ratio (PAPR) in orthogonal frequency division multiplexing (OFDM) system. This method is to divide the input block of OFDM signal into many sub blocks and lower the peak power by weighting the phase of each sub blocks properly. Also, it is applicable for all kinds of OFDM system regardless of the modulation types and the number of subcarriers. Unlike the PTS (partial transmit sequence) and SLM (selective mapping) method using many IFFTs, the SPW method can be realized by only one IFFT. In this paper, the PAPR reduction performance is novelty examined when the adjacent, interleaved and random sub block partitioning schemes are used in the SPW system. The random sub block partition scheme has the most effective performance among the three schemes. In the SPW system, more sub blocks can effectively reduce the PAPR, but there is a problem that the processing time of iteration is increased. |
| In this paper we propose a new improved PAPR reduction method in the SPW than the first version of SPW [12] and analyse performance when the adjacent, interleaved and random sub block partitioning methods are used. As the number of sub blocks is increased, PAPR can be more reduced. If weighting factors are sequentially produced to reduce the PAPR, processing time is exponentially increased because of the many iteration numbers. To solve this problem, we propose a novel weighting factor combination of the complementary sequence characteristic with threshold technique. |
| Partial transmit sequence (PTS) is one of the most important techniques for reducing the peak to average power ratio (PAPR) in OFDM systems. This paper presents a low complexity PTS scheme by applying a new phase sequence. Unlike the conventional PTS which needs several inverse fast Fourier transform (IFFT) operations, the proposed scheme requires half IFFT operations only at the expense of slight PAPR degradation. Simulation and results are examined with QPSK modulation and OFDM signal and power amplifier with memory effects. |
| Partial transmit sequence (PTS) is one of the most important techniques for reducing the peak to average power ratio (PAPR) in OFDM systems. This paper presents a low complexity PTS scheme by applying a new phase sequence. Unlike the conventional PTS which needs several inverse fast Fourier transform (IFFT) operations, the proposed scheme requires half IFFT operations only at the expense of slight PAPR degradation. Simulation and results are examined with QPSK modulation and OFDM signal and power amplifier with memory effects. |
| An orthogonal frequency division multiplexing (OFDM) system has been proposed as a standard for the mobile communication systems. Despite the advantages of OFDM signals like high spectral efficiency and robustness against ISI, the OFDM signals have some disadvantages among which the main one is the high PAPR. |
PROPOSED WORK
|
| The proposed technique for reducing the high Peak-to-Average Power Ratio (PAPR) in the Orthogonal Frequency Division Multiplexing (OFDM) systems and also to minimize the limitations of the existing technique namely Clipping-Based Active Constellation Extension (CB-ACE) algorithm is “Adaptive Active Constellation Extension (Adaptive ACE) Algorithm”. |
| A. Adaptive Active Constellation Extension (Adaptive ACE) Algorithm |
| The Adaptive Active Constellation Extension (Adaptive ACE) algorithm can be initialized by selecting the parameters namely the target clipping level, denoted by A and the number of iterations, denoted by i. In the first step, the iteration is taken as two i.e., i = 2 and the initial target clipping level is to be taken as A. The main objective of the Adaptive Active Constellation Extension (Adaptive ACE) algorithm for reducing the Peak-to-Average Power Ratio (PAPR) is to control both the clipping level and the convergence factor at each step and thereby minimize the peak power signal whichever is greater than the initial target clipping level. |
| The predetermined clipping level, denoted by A, is related to the target clipping ratio, γ and given is by the equation 1. |
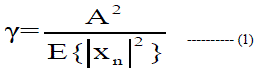 |
| Where, γ – Target Clipping Ratio |
| A – Predetermined Clipping Level |
| xn – Oversampled OFDM signal |
| The clipping of the peak signal results to distortion of the original OFDM signal. The distortion of the original signal can be assumed as the noise, which results to an unreliable communication between the transmitter and the receiver. The distortion caused by clipping the original OFDM signal is categorized into two types, namely – |
| ? In-Band Distortion. |
| ? Out-of-Band Distortion. |
| The in-band distortion results in the system performance degradation and cannot be reduced, while, the out-of-band distortion can be minimized by filtering the clipped signals. The signal obtained after filtering the clipped signal is given by the equation 2. |
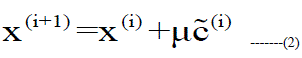 |
| Where,C˜ (i) – Anti-Peak Signal at the ith iteration |
| μ – Convergence Factor |
| The Convergence Factor (CF), denoted by μ can be estimated by using the equation 3. |
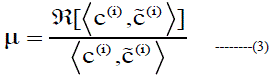 |
| Where, μ – Convergence Factor |
| R – Real Part |
| C(i) – Peak Signal above the Pre-Determined Level |
| C˜ (i)– Anti-Peak Signal at the ith iteration |
| , – Complex Inner Part |
| The anti-peak signal at the ith iteration generated for the PAPR reduction, denoted by (i) C˜ (i) is given by the equation 4. |
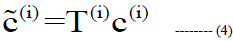 |
| Where, C˜ (i)– Anti-Peak Signal at the ith iteration |
| T(i) – Transfer Matrix at the ith iteration |
| C(i) – Peak Signal above the Pre-Determined Level |
| The transfer matrix at the ith iteration, denoted by T (i), used for generating the anti-peak signal is given by the equation 5. |
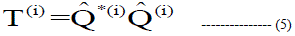 |
| Where, T(i) – Transfer Matrix at the ith iteration |
| |
 |
| The original Orthogonal Frequency Division Multiplexing (OFDM) signal, denoted by xn, is to be clipped in order to reduce the peak signals. The clipping signal is given by the equation 6. |
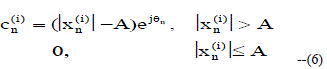 |
| A – Predetermined Clipping Level |
| θn – arg(- (i) n x ) |
| The clipping level, denoted by A, for the next iteration is given by the equation 7 . |
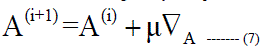 |
| Where, A(i+1) – Next Iteration Level |
| A(i) – Present Iteration Level |
| μ – Convergence Factor |
| ∇A – Gradient with respect to A |
| The gradient with respect to the target clipping ratio, denoted by ∇A , is given by the equation 8. |
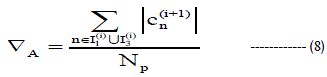 |
| Where, ∇A – Gradient with respect to A |
| Np – Number of peak samples larger than A |
| The Peak-to-Average Power Ratio (PAPR) is to be calculated to the signal which reduces the PAPR than the PAPR calculated for the original OFDM signal or PAPR obtained of the OFDM signal obtained by using the Clipping-Based Active Constellation Extension (CB-ACE) algorithm. |
| B. Calculation of PAPR & CCDF by using Adaptive ACE Algorithm |
| The Peak-to-Average Power Ratio by the Adaptive Active Constellation Extension (Adaptive ACE) algorithm is to be calculated for the Orthogonal Frequency Division Multiplexing (OFDM) signal which is obtained after filtering the clipped signal. |
| C. Calculation of SNR & BER by using Adaptive ACE Algorithm |
| The clipped and filtered OFDM signal is obtained by using Adaptive Active Constellation Extension (Adaptive ACE) algorithm is to be transmitted via an Additive White Gaussian Noise (AWGN) channel, in order to calculate the Signal-to-Noise Ratio (SNR) and Bit Error Rate (BER). The performance of the out-of-band distortion is also examined with the existence of nonlinear PA. By applying both PAPR reduction and DPD the PSD of the output signal is further suppressed. This results in enhancement of power efficiency and therefore less power consumption and more battery life. The proposed method can be applied in recent wireless communications systems such as WiMAX and long term evolution (LTE). |
| D. Advantages of Adaptive ACE Algorithm |
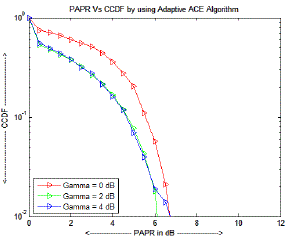
| The Adaptive Active Constellation Extension (Adaptive ACE) Algorithm reduced the Peak-to-Average Power Ratio (PAPR) of the Orthogonal Frequency Division Multiplexing (OFDM) systems by 3.2 dB, 1.7 dB and 1.2 dB for target clipping ratio of 4 dB, 2 dB and 0 dB respectively, at Complimentary Cumulative Distribution Function (CCDF) of 10-2 [3] . Therefore, the problem of low target clipping ratios faced by the Clipped-Based Active Constellation Extension (CB-ACE) Algorithm is resolved. |
| E. Limitations of Adaptive ACE Algorithm |
| The Peak-to-Average Power (PAPR) of the Orthogonal Frequency Division Multiplexing (OFDM) systems is reduced by using Adaptive Active Constellation Extension (Adaptive ACE) Algorithm but the limitation of the transform is the increase in the Bit Error Rate (BER) when compared with the original OFDM signal. The other major limitation of the Adaptive ACE Algorithm is the decrease in the Signal-to-Noise Ratio (SNR). |
RESULTS & DISCUSSION
|
| The Clipping-Based Active Constellation Extension (CB-ACE) Algorithm uses clipping and filtering process in order to generate an anti-peak signal. Then, the PAPR basic formula is used for different values of target clipping ratios (γ = 4, 2, 0). The Peak-to- Average Power Ratios (PAPR) for the target clipping ratios of 4 dB, 2 dB and 0 dB are 8.0 dB, 8.5 dB and 10.0 dB respectively shown in figure 1 |
| The Signal-to-Noise Ratio (SNR) of the Orthogonal Frequency Division Multiplexing (OFDM) signal obtained by the Clipping-Based Active Constellation Extension (CB-ACE) Algorithm is 12 dB at a Bit Error Rate of 10-0.4. In other words, a total of 398- bits are in error when a stream of 1000-bits is transmitted via a communication channel or medium for the original OFDM signal. |
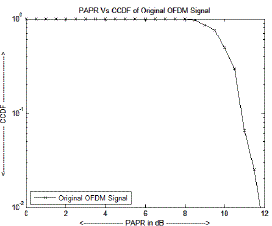
| The Peak-to-Average Power Ratio (PAPR) of the Orthogonal Frequency Division Multiplexing (OFDM) system is equal to 11.8 dB (approximately 12 dB) without using any algorithm i.e., by using the basic formula of PAPR for the original OFDM signal. The existing techniques for reducing the high Peak-to-Average Power Ratio (PAPR) of the OFDM systems are Clipping-Based Active Constellation Extension (CB-ACE) Algorithm and Exponential Companding Transform. |
| The Clipping-Based Active Constellation Extension (CB-ACE) Algorithm uses clipping and filtering process in order to generate an anti-peak signal. Then, the PAPR basic formula is used for different values of target clipping ratios (γ = 4, 2, 0). The Peakto- Average Power Ratios (PAPR) for the target clipping ratios of 4 dB, 2 dB and 0 dB are 8.0 dB, 8.5 dB and 10.0 dB respectively shown in figure 2. From the PAPR values for different target clipping ratios, it is very clear that the PAPR increases when the value of the target clipping ratio is reduced, which results to low clipping ratio problem. The low clipping ratio problem means minimum PAPR cannot be achieved for low target clipping ratios. |
| The Exponential Companding Transform compands the original OFDM signal i.e., compresses the peak signals and expands the small signals. Then the PAPR basic formula is applied on the companded signal. The Peak-to-Average Power Ratio (PAPR) is reduced to 4.5 dB by using the Exponential Companding Transform shown in figure 3. |
| The proposed method i.e., the Adaptive Active Constellation Extension (Adaptive ACE) algorithm reduced the Peak-to- Average Power Ratio (PAPR) to 6.8 dB for all the target clipping ratios, which says that the low target clipping ratio problem faced by the CB-ACE algorithm is eliminated completely |
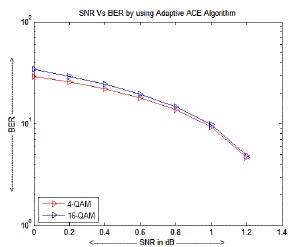
| The Peak-to-Average Power Ratio of the Orthogonal Frequency Division Multiplexing systems is reduced or minimized by using the existing methods namely Clipping-Based Active Constellation Extension (CB-ACE) Algorithm, Exponential Companding Transform and the proposed method namely Adaptive Active Constellation Extension (Adaptive ACE) Algorithm at a Complimentary Cumulative Distribution Function of 10-2 or 0.01. Signal-to-Noise Ratio (SNR) of the original Orthogonal Frequency Division Multiplexing (OFDM) signal is equal to 16 dB at a Bit Error Rate of 10-1. In other words, a total of 100-bits are in error when a stream of 1000-bits is transmitted via a communication channel or medium for the original OFDM signal. |
| The Signal-to-Noise Ratio (SNR) of the Orthogonal Frequency Division Multiplexing (OFDM) signal obtained by the Clipping-Based Active Constellation Extension (CB-ACE) Algorithm is 12 dB at a Bit Error Rate of 10-0.4. In other words, a total of 398- bits are in error when a stream of 1000-bits is transmitted via a communication channel or medium for the original OFDM signal. Signalto- Noise Ratio (SNR) of the companded Orthogonal Frequency Division Multiplexing (OFDM) signal obtained by the Exponential Companding Transform is 12 dB at a Bit Error Rate of 10-0.9. In other words, a total of 126-bits are in error when a stream of 1000-bits is transmitted via a communication channel or medium for the original OFDM signal. |
| The Signal-to-Noise Ratio (SNR) of the Orthogonal Frequency Division Multiplexing (OFDM) signal obtained by the Adaptive Active Constellation Extension (Adaptive ACE) Algorithm is 1.2 dB at a Bit Error Rate of 10-0.4. In other words, a total of 398-bits are in error when a stream of 1000-bits is transmitted via a communication channel or medium for the original Orthogonal Frequency Division Multiplexing (OFDM) signal. |
| From the table 2, the Signal-to-Noise Ratio (SNR) of the OFDM signal is reduced by using the PAPR reduction techniques like Clipping-Based Active Constellation Extension (CB-ACE) Algorithm and Exponential Companding Transform but the SNR is drastically reduced by using the Adaptive Active Constellation Extension (Adaptive ACE) Algorithm. From the table 2, the Bit-Error Rate (BER) of the OFDM signal is drastically increased by using the PAPR reduction techniques like Clipping-Based Active Constellation Extension (CB-ACE) Algorithm and Adaptive Active Constellation Extension (Adaptive ACE) Algorithm but the BER is slightly increased by using the Exponential Companding Transform, when compared with the original OFM signal. |
CONCLUSION
|
| A new phase sequence of PTS scheme has been proposed in this paper. In this approach matrix of possible random phase factors are first generated and then multiplied point-wise with the input signal. By applying this technique the number of IFFT operation is halved which results in lower complexity compared to C-PTS at the expense of slightly PAPR degradation. The performance of the out-of-band distortion is also examined with the existence of nonlinear PA. By applying both PAPR reduction and DPD the PSD of the output signal is further suppressed. This results in enhancement of power efficiency and therefore less power consumption and more battery life. The proposed method can be applied in recent wireless communications systems such as WiMAX and long term evolution (LTE). |
Tables at a glance
|
 |
 |
| Table 1 |
Table 2 |
|
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
References
|
- S. H. Han and J. H. Lee, “An overview of peak-to-average power ratio reduction techniques for multicarrier transmission,” IEEE Wireless Commun., vol. 12, no. 2, pp. 56-65, Apr. 2005.
- L. J. Cimini and N. R. Sollenberger, “Peak-to-average power ratio reduction of an OFDM signal using partial transmit sequences,” IEEE Commun. Lett., vol. 4, no. 3, pp. 86–88, March. 2000.
- R. Buml, R. Fischer, and J. Huber, “Reducing the Peak to Average Power Ratio of Multicarrier Modulation by Selected Mapping,” Elect. Lett, vol. 32, no. 22, pp. 2056-2057, October 1996.
- L. Yang, R. S. Chen, Y. M. Siu, and K. K. Soo, “PAPR reduction of an OFDM signal by use of PTS with low computational complexity,” IEEE Trans. Broadcast., vol. 52, no. 1, pp. 83-86, March 2006.
- S. G. Kang, J. G. Kim, and E. K. Joo, “A novel subblock partition scheme for partial transmit sequence OFDM,” IEEE Trans. Broadcast., vol. 45, no. 3, pp. 333–338, September 1999.
- 6 . N.T Hieu., S.W. Kim and H.G Ryu, “PAPR Reduction of the Low Complexity Phase Weighting Method in OFDM Communication Syst em”, IEEE Trans. on Consumer Electronics, vol. 51, no. 3, pp. 776-782, 2005.
- H. G Ryu., and K. J Youn, “A new PAPR reduction scheme: SPW (subblock phase weighting),” IEEE Trans. on Consumer Electronics, vol. 48, no. 1, pp. 81 – 89, 2002.
- C. Tellambura, “Improved phase factor computation for the PAR reduction of an OFDM signal using PTS,” IEEE Commun. Lett., vol. 5, no. 4, pp.135-137, Apr. 2001.
- P. Varahram, W. A. Azzo, B. M. Ali, “A Low Complexity Partial Transmit Sequence Scheme by Use of Dummy Signals for PAPR Reduction in OFDM Systems,” IEEE Trans. Consumer Electron, vol. 56, no. 4, pp. 2416-2420, Nov. 2010.
- D. H. Park and H. K. Song, “A new PAPR reduction technique of OFDM system with nonlinear high power amplifier,” IEEE Trans. Consumer Electr., vol. 53, no. 2, pp. 327-332, May 2007.
- P. Varahram, S. Mohammady, M. N. Hamidon, R. M. Sidek and S. Khatun, “Digital Predistortion Technique for Compensating Memory Effects of Power Amplifiers in Wideband Applications”, Journal of Electrical Engineering, vol. 60, no. 3, 2009.
- P. B Kenington, High-Linearity RF Amplifier Design. Norwood, MA, Artech House, 2000.
- S. Mohammady, P. Varahram, R. M. Sidek, M. N. Hamidon and N. Sulaiman, “Efficiency improvement in microwave power amplif iers by using Complex Gain Predistortion technique,” IEICE Electronics Express (ELEX), vol. 7, no. 23, pp.1721-1727, Oct. 2010.
- R. J. Baxley and T Zhou., “Comparing slected mapping and partial transmit sequence for PAPR reduction”, IEEE Trans. Broadcast., vol. 53, no. 4, pp.797-803, December 2007.
|