ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Dr.J.M.Mathana1 S.Gunasekar2, S.Jagadish3, R.Karthik4
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
The sensor nodes of a wireless sensor network (WSN) are typically required to maintain sporadic but reliable data transmissions for extended periods of time. However, in applications the sensor nodes have to be small, preventing the use of bulky batteries. The outstanding forward error correction capabilities of turbo codes made them part of many today’s communications standards. And also turbo codes have recently been considered for energyconstrained wireless communication applications, since they facilitate low transmission energy consumption. In this paper, a new low complexity ACS (add compare and select) architecture is introduced in the proposeddesign.The proposed turbo decoder is based on the LUT-Log-BCJR architecture.Entire decoder architecture is coded using Verilog HDL and it is synthesized using Xilinx EDA with Spartan 3E FPGA
Keywords |
| BMU, SMU, LCU, ACS, SISO. |
INTRODUCTION |
| Wireless Sensors are operated for extended periods of time, while relying on batteries that are small, lightweight and inexpensive. So Wireless Sensor Networks (WSN) can be considered to be energy constrained wireless scenarios. In environmental monitoring WSNs for example, despite employing low transmission duty cycles and low average throughputs of less than 1 Mbit/s [1], [2], the sensors’ energy consumption is dominated by the transmission energy. For this reason, turbo codes have recently found application in these scenarios [3], [4], since their near-capacity coding gain facilitates reliable communication when using reduced transmission energy. |
| The architecture oflow complexity reconfigurable turbo decoder is [5]based on branch metric normalization to improve the speed of operation of the decoder. The power consumption of the device for various constraint lengths is measured; the key power-saving technique in the work is the use of decoder run-time dynamic reconfiguration of different constraint lengths. Scalable system architecture for high-throughput turbo-decoders [6] explores a new design space for Turbo-Decoder both under system design and deep-submicron implementation aspects. Two different parallel architectural approaches in terms of performance and implementation complexity are compared in [7]. Both architectures exploit the well-known windowing scheme. An innovative architecture of a block turbo decoder which enabled the memory blocks between all half-iterations to be removed is presented in [8] |
| 3GPP LTE compliant Turbo decoder accelerator presented in [9] takes advantage of the processing power of GPU to offer fast Turbo decoding throughput. This decoder decode multiple code words simultaneously, divide the workload for a single code word across multiple cores, and pack multiple code words to fit the single instruction multiple data (SIMD) instruction width. Area-Efficient high-throughput MAP Decoder Architectures [10] presented a blockinterleaved pipelining (BIP) as a new high-throughput technique for MAP decoders. |
II. CONVENTIONAL LUT-LOG-BCJR ARCHITECTURE |
| The energy consumption of conventional LUT-Log-BCJR architectures cannot be significantly reduced by simply reducing the frequency and throughput. This motivates a new architecture which is specially designed to reduce the hardware complexity and thereby reducing the energy consumption. The turbo decoder structure shown in figure 1 consists of two soft-input soft-output (SISO) decoders and an interleaver / deinterleaver between them. Decoding process in a turbo decoder is performed iteratively through the two SISO decoders via the interleaver and the deinterleaver. |
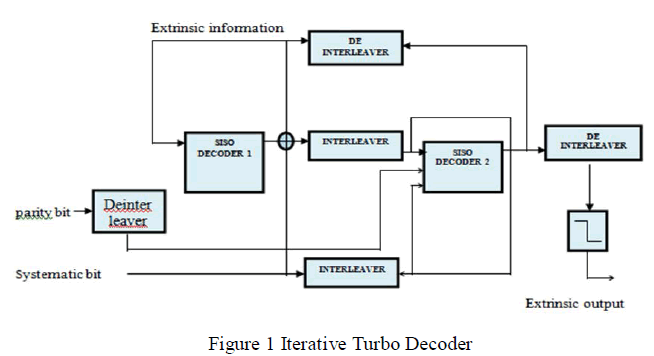 |
| The first decoder will decode the sequence and pass the hard decision together with a reliability estimate of this decision to the next decoder after proper interleaving. It is possible to decode Turbo codes by first independently estimating each process and then refining the estimates by iteratively sharing information between two decoders, since the two processes run on the same input data. More specifically, the output of one decoder can be used as the apriori information by the other decoder. It is necessary for each decoder to produce soft-bit decisions in order to take advantage of this iterative decoding scheme. Considerable performance gain can be achieved in this case, by executing multiple iterations of decoding. |
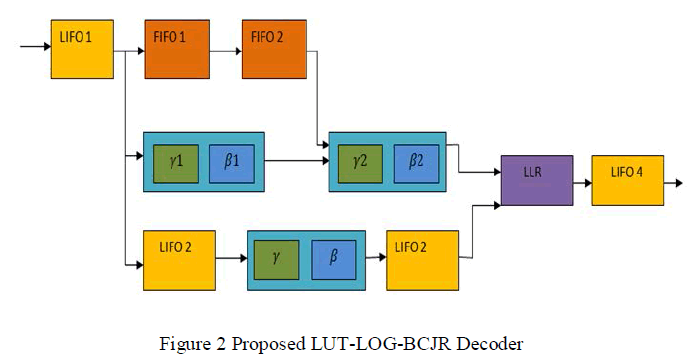 |
| The proposed SISO decoder is shown in figure 2. It consists of the forward and backward state metric, LLR computation, and memory (LIFO and FIFO) blocks. LIFO and FIFO memory blocks are used to control the flow of input symbol data .The LIFO 1 and 2, and the FIFO 1 and 2 are used to buffer the input data symbols. The LIFO 3 and 4 are to store the forward state metric and the LLR values, respectively. The SISO decoder has been built with two backward state metric units, β1 and β2, where β1 is ‘dummy logic’. It is used to provide the state metric value to β2, which generates the backward state metric to compute the LLR values. ‘ α’ and ‘γ’ denote the forward state and branch metric units to calculate the forward state and branch metric values. |
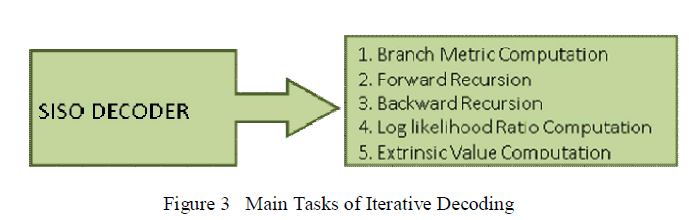
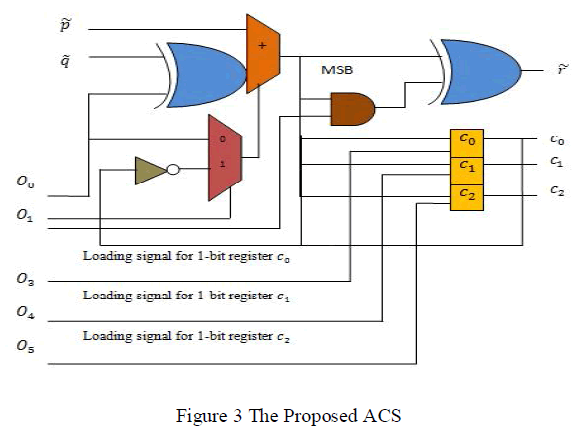
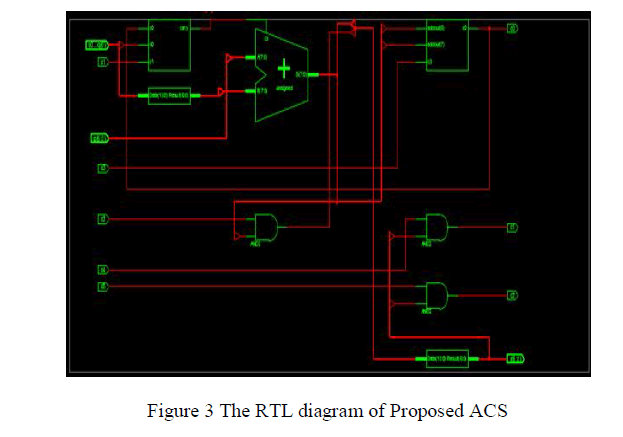
| Each decoder has a number of computational intensive tasks to be done during decoding. There are five main computations to be performed during iteration in the decoding stage as shown in figure 3. |
 |
III. BRANCH METRIC UNIT |
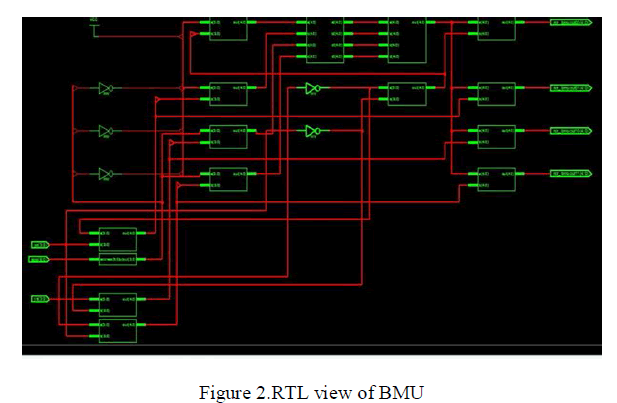
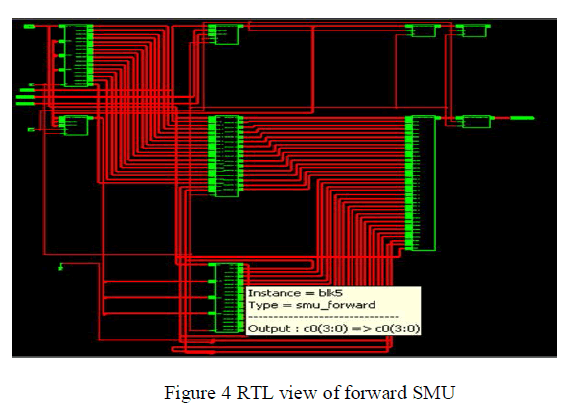
| The proposed BMU computes the branch metric values from the input data symbols. The generated branch metric are converted into absolute values, which are then compared to the maximum or minimum branch metric values to get the normalized value. Conventionally the state metric values are normalized but in the proposed design branch metric values are normalized. The RTL diagram of the proposed BMU is shown in figure 4. |
 |
IV. STATE METRIC UNIT |
| The next step of computation is state metric values. The basic building block of state metric unit (SMU) is ACS.It is a simple Look-Up Table (LUT) is used to minimize the errors caused by the Jacobi approximation.The forward state metric value is ‘α’ given by |
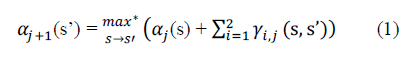 |
| where, s – s’ represents the set of all states s that can transition into the state s’. The max* operation is used to represent the Jacobian logarithm detailed in [12], which may be approximated using a Look-Up Table (LUT) [11] for the parameters p and q . |
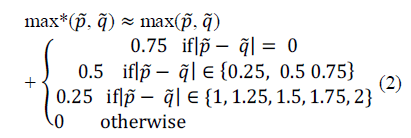 |
| The backward state metric ïÿýïÿý is given by |
| Observe that Equations (1), (2) and (3) of the LUT-Log-BCJR algorithm comprise only additions, subtractions and the max* calculation of Equation (2). While each addition and subtraction constitutes a single ACS operation, each max* calculation can be considered equivalent to four ACS operations, as shown in Table I. |
| Table I Decomposition Of Max* Operation |
 |
 |
 |
 |
 |
| The forward state metric is the next step of computation in the algorithm which represents the probability of a state at time ‘k’ given the probabilities of states at previous time instance. It is calculated using equation (1). The backward state probability being in each state of the trellis at each time ‘k’, given the knowledge of all the future received symbols is recursively calculated and stored. |
 |
| The backward state metric is computed using Equation (3) in the backward direction going from the end to the beginning of the trellis at time instance ‘k-1’, given the probabilities at time instance ‘k’. The backward state metric computation can start only after the completion of the computation by the branch metric unit. State Metric value for a particular node is computed based on the trellis diagram of the encoder. In the SMU, the add compare select (ACS) units are recursively processed to compute the state metrics, through the connection network that allocates the state metrics for the next ACS based on the current constraint length ‘K’ value. For a particular constraint length ‘K’, this state metric allocation must be done before they are fed as input to the ACS in the next clock cycle. |
V. LLR COMPUTATIONAL UNIT |
| Log likelihood ratio is the output of the turbo decoder. The LLR for each symbol at time ‘k’ is calculated using the Equation (5). |
 |
| The main operations involved in LLR computation are comparison, addition and subtraction. Finally these values are de-interleaved at the second decoder output after the required number of iterations to make the hard decision in order to retrieve the information that is transmitted. The sign of the number corresponds to the hard decision while the magnitude gives a reliability estimate. In order to compute LLR value, forward; backward state metric values and branch metric values of all states are required. |
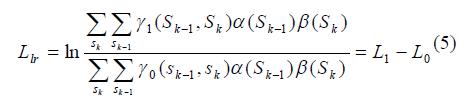 |
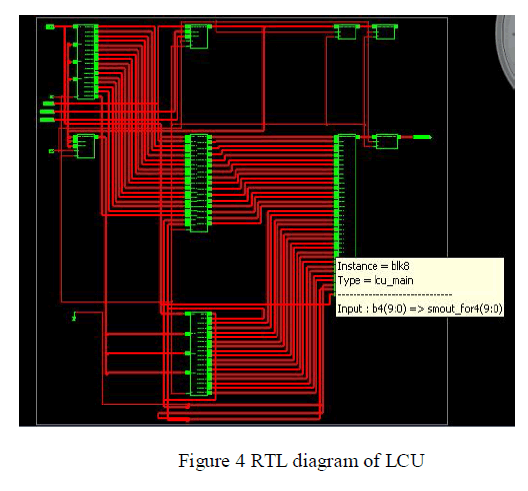
| The RTL diagram of LCU is shown in figure 4. |
VI. RESULT AND DISCUSSION |
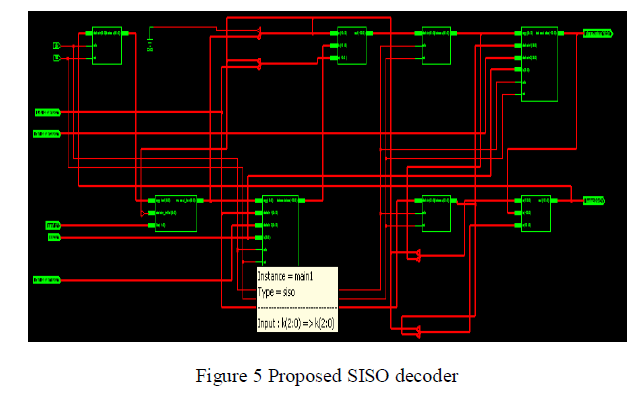
| The Verilog code for the proposed turbo decoder is synthesized using Xilinx EDA tool. The RTL view and the simulation result of SISO decoder is shown in the figure 5. |
 |
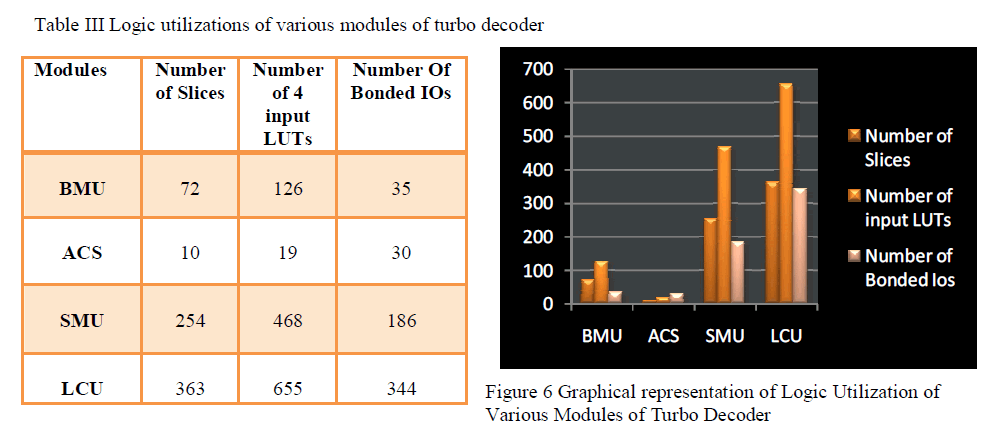 |
| It is observed that from the table III that more number of slices are utilized by LCU unit. |
 |
VII. CONCLUSION |
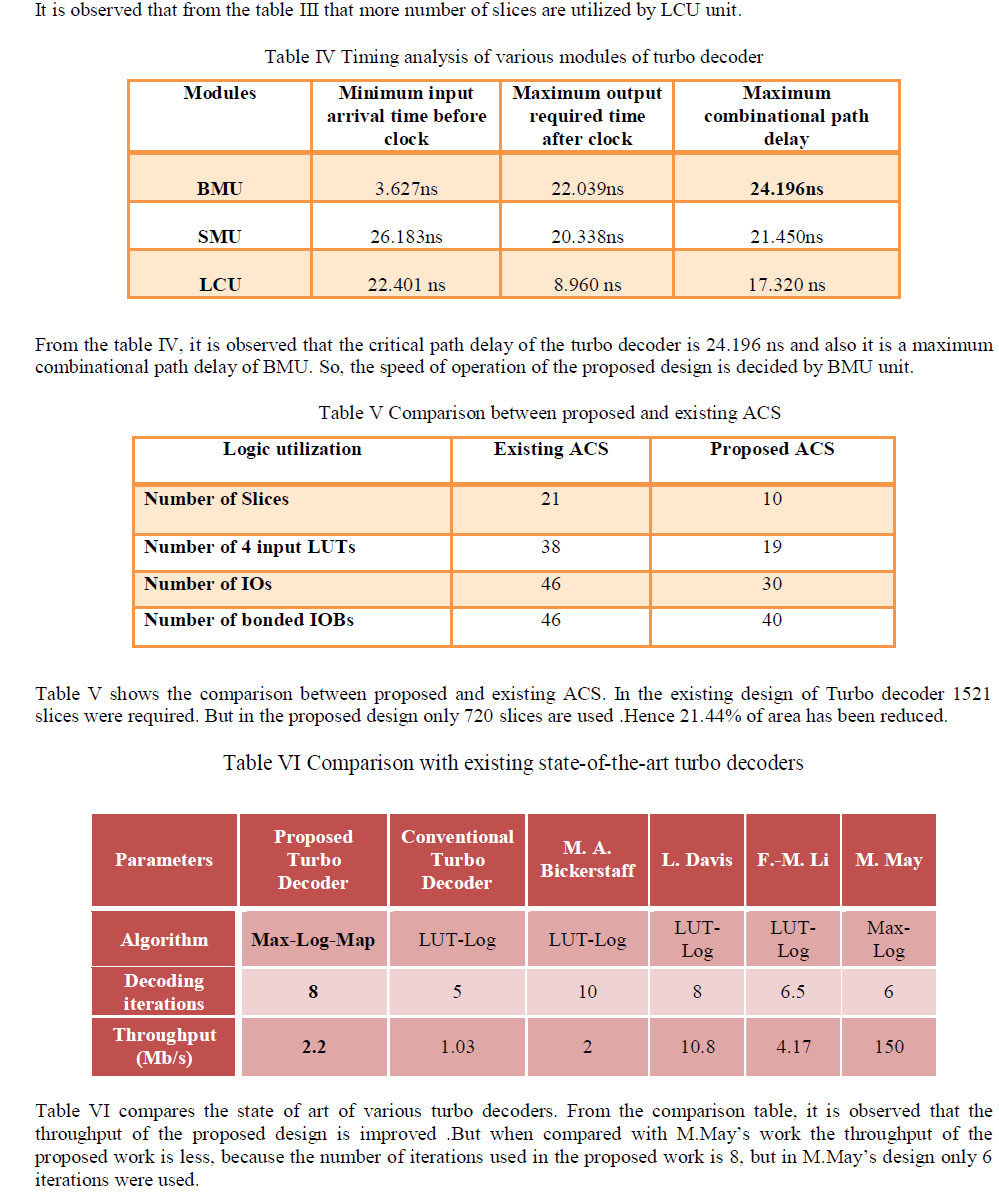
| In energy-constrained applications, achieving low energy consumption has a higher priority than having a high throughput. This motivated our low-complexity energy-efficient architecture, which achieves a low area and hence a low energy consumption by decomposing the LUT-Log-BCJR algorithm into its most fundamental ACS operations.Hence the turbo decoder architecture is designed in such a way that the area is reduced by 21.44% and the speed is improved by 28.1% while the throughput is 2.2 Mbps and thereby reducing the complexity.This entire architecture is implemented in Application Specific Integrated Circuit (ASIC) and this will improve the speed and reduce the area further. |
References |
|