Keywords
|
| Modified Booth Encoding, higher speed, lower cost, and less VLSI area. |
INTRODUCTION
|
| In the binary numeration system the digits, known as bits, square measure restricted to the set [0, 1]. The results of multiplying any binary range by one binary bit are either zero, or the initial range. This makes forming the intermediate Partial-products straightforward and economical. Summing these partial-products is that the time intense task for binary multipliers. One logical approach is to create the partial-products one at a time and add them as they’re generated. |
| Typically enforced by computer code on processors that don't have a hardware number, this system works fine, however is slow as a result of a minimum of one machine cycle is needed to add every extra partial-product. For applications wherever this approach doesn't offer enough performance, multipliers may been forced directly in hardware .Booth multiplication may be a technique that permits for smaller, quicker multiplication circuits, by coding the numbers that square measure increased. it's the quality technique utilized in chip style, and provides vital enhancements over the "long multiplication" technique. |
RELATED WORK
|
| Reversible logic has received nice attention within the recent years because of their ability to cut back the ability dissipation that is that the main demand in low power VLSI style. Quantum computers are made victimization reversible logic circuits. It’s wide applications in low power CMOS and Optical informatics, DNA computing, quantum computation and applied science. In 1973, C. H. Bennett [1,3] over that no energy would be dissipated from a system as long because the system was able to come to its initial state from its final state in spite of what occurred in between. It created clear that, for power to not be dissipated within the discretionary circuit, it should be engineered from reversible gate. Reversible circuits are of explicit interest in low power CMOS VLSI style. In 1960 R.Landauer incontestable that top technology circuits and systems made victimization irreversible hardware end in energy dissipation because of info loss [1]. The warmth generated because of the loss of 1 little bit of info is extremely little at temperature however once the amount of bits is a lot of as within the case of high speed machine works the warmth dissipated by them are going to be thus giant that it affects the performance and ends up in the reduction of period of the elements. In 1973, Bennett, showed that one will avoid KTln2 joules of energy dissipation constructing circuits victimization reversible logic gates [2]. A reversible computer circuit is associate n-input n-output logic device with matched mapping. This helps to work out the outputs from the inputs and additionally the inputs are often unambiguously recovered from the outputs. Additionally within the synthesis of reversible circuits direct fanout isn't allowed as one–to-many construct isn’t reversible. However fan-out in reversible circuits is achieved victimization further gates. |
| A reversible circuit ought to be designed victimization minimum range of reversible logic gates. From the purpose of read of reversible circuit style, there are several parameters for determining the quality and performance of circuits [3, 4 and 13].The amount of Reversible gates (N): the amount of reversible gates employed in circuit. The amount of constant inputs (CI): This refers to the amount of inputs that are to be maintained constant at either zero or one so as to synthesize the given logical perform. Quantum value (QC): This refers to the value of the circuit in terms of the value of a primitive gate. It’s calculated knowing the amount of primitive reversible logic gates (1*1 or 2*2) needed to understand the circuit. Gate levels (GL): This refers to the amount of levels within the circuit that are needed to understand the given logic functions [4]. |
| Reduction of those parameters is that the bulk of the work concerned in coming up with a reversible circuit. During this paper, associate 2 varieties of numbers are intended victimization reversible gates. Multiplier plays a vital role in machine operation victimization computers. There are several arithmetic operations that unperformed, on a laptop ALU, through the utilization of multipliers. Style and implementation of digital circuit’s victimization reversible logic has attracted quality to realize entry into the long run computing technology [20]. |
| Wallace trees and linear arrays each need roughly one CSA for each partial product to be reduced. Similarly, 4-2 trees need one 4-2 adder for each 2 partial merchandise [17]. Thus, just like the alternative structures, 4-2 trees are large. One answer to the dimensions downside is to use a partial 4-2 tree. As an example, a sixty four bit quantity may be increased in four items employing a sixteen X 64bit partial 4-2 tree. The four partial results are then summed to create the complete result. One performance limiting issue of this technique is the latency through the 4-2 tree [20]. |
| The primary sixteen X sixty four bit partial multiply should flow through the whole 4-2 tree before successive partial multiply may be started down the array. The solution to the latency downside lies with higher hardware utilization. |
| Though the latency for the first partial multiply through the tree would be slightly longer because of the added latches, ensuing partial results arrive on every 4-2 cycle thenceforth. The result is that a lot of less time is needed to get all of the partial results. |
| This paper is organized as follows: Section two provides the temporary introduction of the Radix 4 booth encoding. Section three and four describes the planning of number circuit and also the implementation of the projected number circuit victimization new reversible gates. Section five provides the results and discussions and also the comparative study of style with the projected style. |
RADIX-4 BOOTH ENCODING
|
| In Radix-4 Booth coding assumes that x and y square measure bit vectors of widths n-1 and 2m- 1, severally. Number splits economical computation of x.y as an add of partial product. Conceptually, the number is partitioned off into 2-bit slices, y[2i+1:2i] ,i=0 ,..,m-1 Corresponding to each slice, we define an integer encoding θi in the range -2≤ θ ≤ 2 For y €N and i € N, |
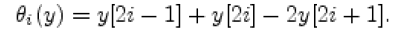 |
a. Reducing the Number of Partial Products in Multiplier
|
| It is doable to cut back the amount of partial product by [*fr1], by exploitation the technique of number four Booth secret writing. The essential plan is that, rather than shifting and adding for each column of the number term and multiplying by one or zero, |
| PP 0 = M * -1, shift left 0 bits (x -1) |
| PP 1 = M * 2, shift left 2 bits (x 8) |
| The result is equaling shift and add method: |
| PP 0 = M * 1, shift left 0 bits (x 1) |
| PP 1 = M * 1, shift left 1 bits (x 2) |
| PP2 = M * 1, shift left 2 bits (x 4) |
PP3 = M * 0, shift left 3 bits (x 0)
|
| The advantage of this methodology is that the halving of the quantity of partial product. This is often necessary in circuit style because it relates to the propagation delay within the running of the circuit, and also the complexness and power consumption of its implementation. |
MULTI-OPERAND ADDERS
|
| Multiplier partial merchandise accumulation depends on completely different set of hardware algorithms that maybe chosen for multi-operand adders, wherever the bit-level optimized style indicates that the matrix of partial product bits is reorganized to optimize the amount of basic parts. |
1. Carry-Look-Ahead Adder
|
| The ripple-carry adder having terribly slowed once one must add several bits. There in a 32-bit adder, the delay would be regarding sixty three ns if one assumes a gate delay of one ns. |
| The carry-look-ahead adder solves this downside by shrewd the carry signals earlier, supported the input signals. It’s supported the actual fact that a carry signal is going to be generated in 2 cases: |
| 1) When both bits Ai and Bi are 1, (2) When one of the two bits is 1 and the carry-in is 1. |
| C1 =G0 +P0.C0 |
| C2 =G1 +P1.C1 =G1 +P1.G0 +P1.P0.C0 |
| C3 =G2 +P2.G1 +P2.P1.G0 +P2.P1.P0.C0 |
| C4 = G3 + P3.G2 + P3.P2.G1 + P3P2.P1.G0 + P3P2.P1.P0.C0 |
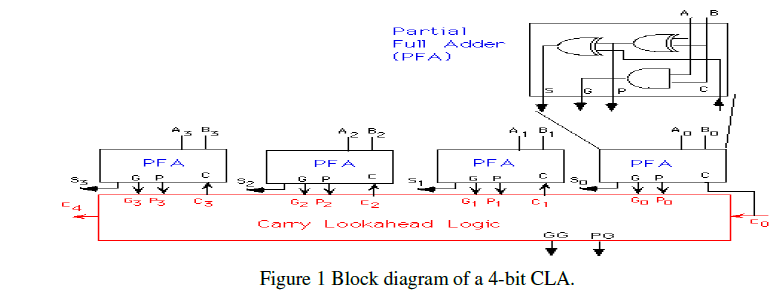 |
2. Block carry look-ahead adder
|
| Carry look-ahead adder is to reverse the basic design principle of the RCLA, that is, to ripple carries within blocks but to generate carries between blocks by look-ahead. A block carry look-ahead adder [20]. |
 |
3. Proposed TG Method
|
| The results of the previous sections can be summarized in the following four statements: |
| 1. Spurious activity limits number efficiency. |
| 2. Wallace reduces defect generation and propagation. |
| 3. Minimum-size transistors increase energy efficiency. |
| 4. An additional refined approach (Chong) so succeeds in decreasing the spurious activity . |
| However, of an oversized energy over head and technology dependent junction transistor level techniques. During this planned Transmission gate number, the reversible transmission gate. The Transmission Gate is low power consumption reversible gate is employed as a result of it uses only 2 transistors however the gate uses six transistors. The total adder is meant by victimization the two peres gate. The total adder victimization reversible peres gate is shown in fig.1 |
| TG-Multiplier could be a straightforward design supported the Wallace tree with minimum-size transistors. The Reversible Transmission gates that make the terms are enforced in level-restoring static CMOS that gift strictly electrical phenomenon inputs, thence decoupling the number from the input drivers. The full-adder is build of 2 reversible peres gate. The full-adder cells within the final RCA are once more level-restoring static CMOS gates to recover the driving capability. |
RESULTS AND DISCUSSIONS
|
| The simulation obtained using Altera quatrus II environment, Multiplier energy potential is that the results of careful trade-off among many, typically different factors, from discipline all the way down to semiconductor device level. The new multiplier factor structure introduced during this work (TG-Multiplier) succeeds in reducing spurious change activity considerably while not compromising the advantages with energy-hungry add-on sub circuits. |
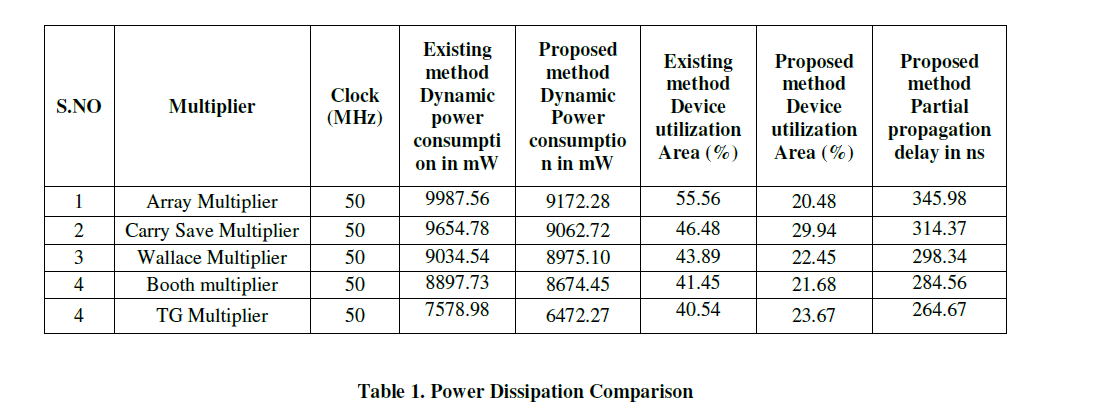
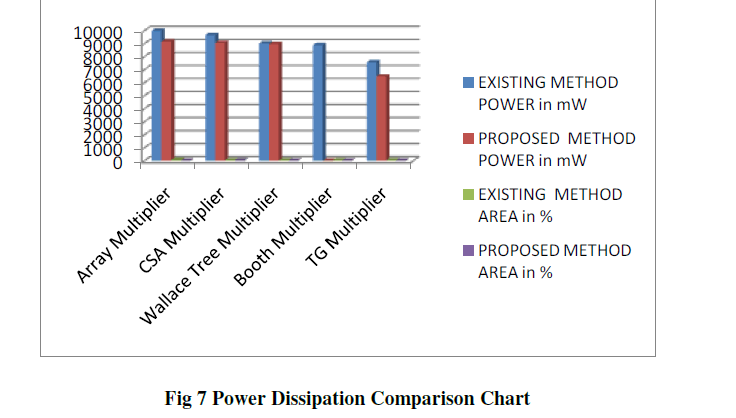
| Transmission gates combined with level-restoring static CMOS Reversible Logic Peres gates, suppress glitches via RC low-pass filtering, whereas conserving timeless driving capabilities. The table 1 shows the power comparison and area utilization report. The proposed TG reversible logic based multiplier having less power consumption than others. The Reversible gates are wont to implement arithmetic circuit victimization full Adder and Subtractor and reversible feedback loop for the Adder/Subtractor. In figure 3 and 4 Proposed reversible logic multiplier implementation using radix 4 approach. In this paper the reversible logic method tested with all input sequences are maintained as common for all the multiplier circuits. Both the multiplicand and multiplier deicide the reversible logic. |
| The Reversible sixteen bit Reversible number is constructed victimization economical style with minimum quantum price, minimum garbage and minimum space and power overheads. The projected style implementation of Reversible arithmetic unit victimization Reversible number has higher performance as compared to existing styles in terms of range of gates used, Garbage outputs and Quantum price and hence will be used for low power applications. Figure 5 and 6 represents the Wallace tree and transmission gate based multiplier approach that having same set of input and output with reference to the previous multipliers. |
| Reversible Logic implemented using unsigned multiplier and its results comparison shown in table 1 .The static power consumption has less difference with respect to the dynamic power consumption, so they are not included in the table. The proposed reversible logic circuit having the less delay variation with respect to the existing method. All the circuits are verified using different device families in the Altera quatrus II environment with different device setup provides similar variation, they helps to analyze the performance of the proposed method. Reversible logic tested with serial parallel multiplier also. The Reversible logic reduces the computation time and power. |
 |
 |
 |
CONCLUSION
|
| The common multiplication methodology is “add and shift” formula. In parallel numbers range of partial product to be supplemental is that the main parameter that determines the performance of the multiplier. To scale back the quantity of partial product to be supplemental, changed Booth formula is one in all the foremost fashionable algorithms. |
| To realize speed enhancements Wallace Tree formula may be accustomed scale back the quantity of serial adding stages. Any by combining each changed Booth formula and Wallace Tree technique we are able to see advantage of each algorithm in one number. but with increasing correspondence, the quantity of shifts between the partial product and intermediate sums to be supplemental can increase which can lead to reduced speed, increase in chemical element space attributable to irregularity of structure and additionally accrued power consumption attributable to increase in interconnect ensuing from advanced routing. On the opposite hand “serial-parallel” multipliers compromise speed to realize higher performance for space and power consumption. The choice of a parallel or serial number all depends on the character of application. In this paper we tend to studied the multiplication algorithms and design and compare them in terms of speed, area, power and combination of those metrics. |
References
|
- R. Landauer, “Irreversibility and Heat Generation in the Computational Process”, IBM Journal of Research and Development, 5, pp. 183-191, 1961.
- C.H. Bennett, “Logical Reversibility of Computation”, IBM J.Research and Development, pp. 525-532, November 1973.
- T. Toffoli., “Reversible Computing”, Tech memo MIT/LCS/TM-151, MIT Lab for Computer Science (1980).
- E. Fredkin and T. Toffoli, “Conservative logic,” Int’l J. Theoretical Physics, Vol. 21, pp.219–253, 1982.
- R. Feynman, “Quantum Mechanical Computers,” Optics News, Vol.11, pp. 11–20, 1985.
- B. Parhami; “Fault Tolerant Reversible Circuits” Proc. 40th Asilomar Conf. Signals, Systems, and Computers, Pacific Grove, CA,Oct.2006. Peres, “Reversible Logic and Quantum Computers”, Physical review A, 32:3266- 3276, 1985.
- W. N. N. Hung, X. Song, G. Yang, J. Yang and M. Perkowski, “Quantum Logic Synthesis by Symbolic Reachability Analysis”, Proc. 41st annualconference on Design automation DAC, pp.838-841, January 2004.
- M. D. Ercegovac and T. Lang, Digital Arithmetic. Los Altos, CA, USA: Morgan Kaufmann Publishers, 2003.
- S. K. Hsu, S. K. Mathew, M. A. Anders, B. R. Zeydel, V. G. Oklobdzija, R. K. Krishnamurthy, and S. Y. Borkar, “A 110gops/w 16-bit multiplier andreconfigurablepla loop in 90-nm cmos,”IEEE Journal of Solid State Circuits, vol. 41, pp. 256–264, Jan. 2006.
- 1 M. S. Schmookler, M. Putrino, A. Mather, J. Tyler, H. V. Nguyen, C. Roth, M. Sharma, M. N. Pham, and J. Lent, “A low-power, high-speedimplementation of a powerpc(tm) microprocessor vector extension,”Proceedings of the 14th IEEE Symposium on Computer Arithmetic, p. 12, 1999.
- A. D. Booth, “A signed multiplication technique,”Quarterly J. Mech. Appl. Math., vol. 4, 1951.
- L. Dadda, “Some schemes for parallel multipliers,”Alta Frequenza, vol. 34, May 1965.
- O. L. MacSorley, “High speed arithmetic in binary computers,”Proceedings IRE, vol. 49, pp. 67–91, Jan. 1961.
- J.-Y. Kang and J.-L.Gaudiot, “A simple high-speed multiplier design,”IEEE Transactions on Computers, vol. 55, no. 10, pp. 1253–1258, Oct. 2006.
- “A fast and well-structured multiplier,”Proceedings of Euro micro Symposium on Digital System Design, pp. 508–515, Sept. 2004.
- E. M. Schwarz, R. M. A. III, and L. J. Sigal, “A radix-8 cmos s/390 multiplier,”Proceedings of the 13th IEEE Symposium on Computer Arithmetic, p.2, 1997.
- W.-C. Yeh and C.-W. Jen, “High-speed booth encoded parallel multiplier design,”IEEE Transactions on Computers, vol. 49, no. 7, pp. 692–701, Jul.2000.
- Z. Huang and M. D. Ercegovac, “High-performance low-power left-to-right array multiplier design,”IEEE Transactions on Computers, vol. 54, no.3, pp. 272–283, Mar. 2005.
- C. S. Wallace, “A suggestion for a fast multiplier,”IEEE Transactions on Electronic Computers, vol. EC-13, no. 1, pp. 14–17, Feb. 1964.
- V. G. Oklobdzija, D. Villeger, and S. S. Liu, “A method for speed, optimized partial product reduction and generation of fast parallelmultipliersusingan algorithmic approach,”IEEE Transactions on Computers, vol. 45, no. 3, pp. 294–306, Mar. 1996.
- P. F. Stelling, C. U. Martel, V. G. Oklobdzija, and R. Ravi, “Optimal circuits for parallel multipliers,”IEEE Transactions on Computers, vol. 47, no.3, pp. 273–285, Mar. 1998.
- J.-Y. Kang and J.-L. Gaudiot, “A logarithmic time method for two’s complementation,”Proceedings of the Int. Conference on ComputationalScience, pp. 212–219, 2005
|