Performance Evaluation of Various
Controllers Designed for an Industrial First
Order plus Delay Process

Saurabh Rajvanshi; Pradeep Juneja

Performance Evaluation of Various Controllers Designed for an Industrial First Order plus Delay Process

Saurabh Rajvanshi 1, Pradeep Juneja2

M.Tech. Student, Dept. of Electrical & Electronics, Graphic Era University, Dehradun, India
Associate Professor, Dept. of Electrical & Electronics, Graphic Era University, Dehradun, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

As most of the industrial processes can be modeled using first order plus dead time model. A blending process, which can be represented as a FOPDT model, is selected for controller design based on different well established and relatively newer controller tuning methods. Based on comparison of set point tracking capability of the controller and dynamic and steady state characteristics, best controller tuning technique is determined for the process.

Keywords

FOPDT, PID controller, blending process, controller tuning, time response characteristics.

INTRODUCTION

Most of the processes in industry are composed of many dynamic elements that are usually of first order. This leads the overall process to have a linear model of a very high order. Although these higher order models are very precise they are not to be used for the control purposes. Instead of using high order model, behaviour of the process is simply modelled as a linear first order system with the dead time element, in most of the cases [1]. A time delay is generally present in the system which is actually a delay because of transport lag. The dead time may be because of many reasons, especially due to the distant sensor location [2]. It is generally believed that PID controller and its variations (P, PI and PD) is the most commonly used controller in the process control application. Because they can compensate the effect of both the delayed and non delayed process and ease of implementation, these controllers are used in industrial application [3], and more than 90% of existing control loop involve PID controller [4]. Numerous methods have been projected for tuning these controllers, but every method has some constraint [3]. As a result, the design of PID controller still remains a challenge before researchers and engineers. A PID controller has the following transfer function:

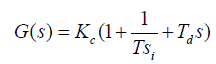The aim of the PID controller tuning is to find out PID parameter c i d (K ,T ,andT ) to meet a given set of a closed loop system performance [6].

The process considered in this work is a simple blending process. In Blending operation, control objective is to mix or blend two input inlet stream and make a final control output to ensure that the final product meet customer specification. A stirred- tank blending process is shown in fig. 1. Stream 1 is a mixture of a two chemical species, A and B such that its mass flow rate w1 is constant, but the mass fraction of A is x1, varies with time. Stream 2 consist of a pure A and thus x2=1. The mass fraction of A in the exit stream is denoted by x and the desired value (set point) by Xsp . Thus for this control problem, the controlled variable is x, the manipulated variable is w2, and the disturbance variable is x1[5].

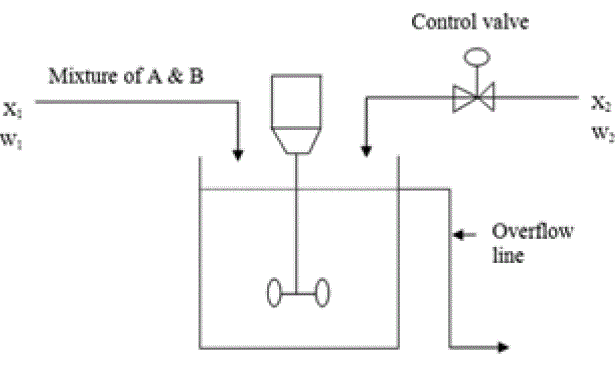
Fig. 1. Stirred Tank Blending System[5]

A large number of industrial processes can approximately be modelled by a FPODT transfer function as:

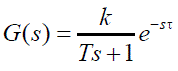Where k is process static gain, τ is the dead time and T is the time constant. To design a PID controller for this type of a processes model, various methods have been suggested during the past sixty year [9].

COMPARISON OF TUNING FORMULAS

There are several examples present in the literature which can be use to evaluate various PID design or tuning methods. Though, the specific method might be effective for a specific plant model or a process, so it is difficult to draw general conclusion that which method is convenient or better for the selected process. What we can bring to a close is that which method show better performance within the process. The performance can be calculated in terms of tuning parameter such as proportional gain constant p K , integral gain constant i T and derivative gain constant d T and based on the time response characteristics such as rise time, setting time, overshoot (%), peak, gain and phase margin and closed loop stability.

1. The process model is first-order with dead time(FOPDT)

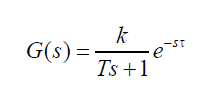2. The following PID tuning formulae are considered as shown in Table I:

• Ziegler-Nichols (Z-N) method has two version i.e. one depend on the reaction curve and the other, the ultimate gain and the ultimate period.

• Cohen-Coon (C-C) method which is based on reaction curve. A model with one tangent and point is derived first to tune the PID controller.

• Internal model control (IMC) method is proposed in Rivera, Morari and Skogested. The smaller it is the better performance the closed-loop system will have. Here the tuning parameter λ is chosen as 0.25τ of the delay, the smallest value suggested in reference [7].

• Saeed and Mahdi proposed formula for ITAE performance index using dimensional analysis and numerical optimization techniques, an optimal method for tuning PID controller for FOPDT model is presented [9]

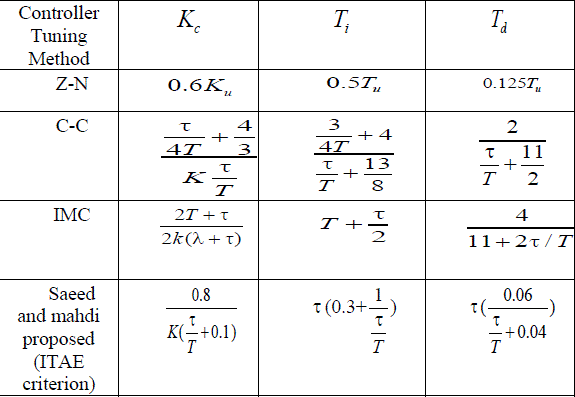
TABLE I PID TUNING FORMULAS

Where λ >0.25 as suggested in Rivera et al and u K is the ultimate gain [7, 9]

METHODOLOGY

Blending operation is commonly used in many industrial to ensure that final product meet customer specification. The transfer function [8] is given as -

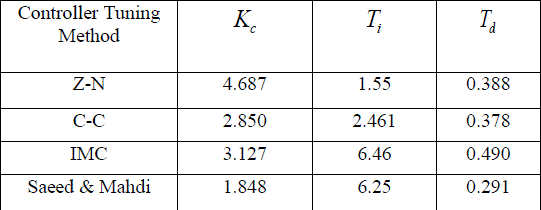
TABLE II PID CONTROLLER PARAMETER

The controller parameter for different controller tuning formulae is shown in table II.

RESULT AND DISCUSSION

Simulation is performed to analyse the set point tracking and the different unit step response characteristics i.e. rise time, settling time, overshoot (%), and closed loop stability. Fig. 2 shows the step responses for the comparison among the values of different controller tuning techniques i.e. Ziegler-Nichol, Cohen-Coon, Internal model control and the Saeed and Mahdi proposed formula.

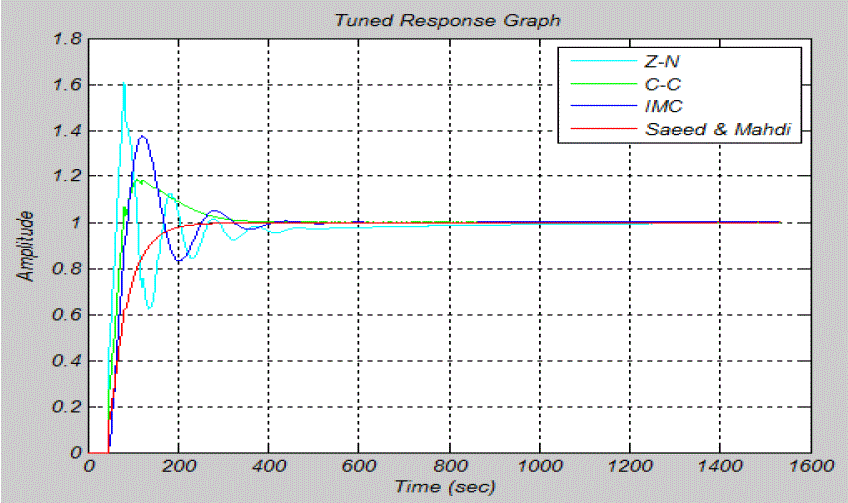
Fig 2: Comparison of responses for different controller design methods

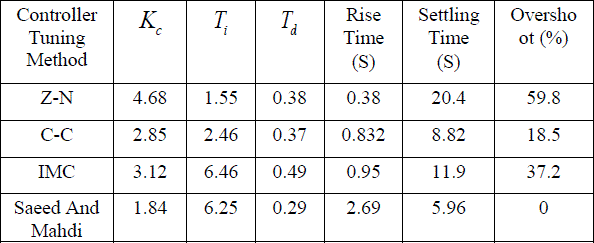
TABLE III COMPARISON OF TIME RESPONSE CHARACTERISTICS

From the Table III it is observed that

• The controller tuned by Z-N and IMC method has large proportional gain in comparison to the C-C method and Saeed and Mahdi proposed method.

• Controller tune by IMC and Saeed and Mahdi proposed method have large integral gains i.e. 6.46 And 6.25 which provide steady state stability to the response.

• The Saeed and Mahdi proposed method have small derivative gain as compare to the other methods.

• Z-N, C-C and IMC provide large settling time i.e. 20.4, 8.82 and 11.9 for the process as compare to Saeed and Mahdi proposed methos which is 5.96.

• The Saeed and Mahdi Proposed method have zero overshoot and good rise time i.e. 2.69 which is requiring for the process than the other selected tuning method.

Form this observation it is clear that controller tuning formula proposed by Saeed and Mahdi, which is relatively new is a better option for control of selected FOPDT process rather than the other controller tuning techniques explored in present investigation.

CONCLUSION

A large number of PID controller tuning rules have been defined for the single input single output process with dead time. Four different types of controller tuning rules are selected to control the selected FOPDT process. The performance evaluation is based on the time response characteristics such as, rise time, settling time and overshoot. The comparison shows that the controller tuned by Saeed and Mahdi proposed method has the best response among all other selected tuning methods.

ACKNOWLEDGMENT

The authors gratefully acknowledge The Department of „Electrical and Electronics engineering’, ‘Graphic Era University’, Dehradun, India for the direct and indirect contribution in the work on the original version of this document.

References

Kurtulan,S., Goren, L., “A design method for a wide class of industrial processes”, Turkish Automatic Control Committee National Congress,October, 2005 (In Turkish).

OÃÂ¢Ãâ¬ÃÅ¸Dwyer , A., “PID compensation of time delayed processes 1998-2002: a survey”, in Proc. American Control Conf., Denver, Colorado,USA, pp. 1494-1499, 2003.

Astrom, K. J., and Hagglund, T., Automatic Tuning of PID Controllers, Instrument Society of America, 1998.

Koivo, H. N., and Tanttu, J. T., “Tuning of PID Controllers: Survey of SISO and MIMO Techniques,” in Proceedings of Intelligent Tuningand Adaptive Control, Singapore, 1991

William S. Levine, W.S (Editor), CRC Control Handbook, Chapter 72, “Control of the Pulp and Paper Making Process”. CRC Press and IEEEPress, - Bialkowski W., Chapter 72, 1996.

Ogata, K., Modern Control Engineering, Prentice Hall, 1997.

Wen Tan, Jizhen Liu , Tongwen Chen, Horacio J. Marquez “Comparison of some well-known PID tuning formulas” Computers and ChemicalEngineering 30 (2006) 1416–1423 in ELSEVER.

Dan Chen and Seborg, Dale E., “PI/PID Controller Design Based on Direct Synthesis and Disturbance Rejection”, Ind. Eng. Chen. Res 2004,41, pp. 4807-4822.

TavakoliSaeed&Tavakoli Mahdi “Optimal tuning of PID controller for first order plus delay models using dimensional” The FourthInternational Conference on Control and Automation (ICCAÃÂ¢Ãâ¬ÃÅ¸03), Montreal, Canada, 10-12 June 2003.