INTRODUCTION
|
| Recent multimedia applications for handheld and portable devices place a limit on the available wireless bandwidth. Wavelet based techniques such as JPEG2000 for image compression has a lot more to offer than conventional methods in terms of compression ratio. Flexible energy-efficient hardware implementations that can handle multimedia functions such as image processing, coding and decoding are critical, especially in hand-held portable multimedia wireless devices. Wavelets are mathematical functions defined over a finite interval and having an average value of zero that transform data into different frequency components, representing each component with a resolution matched to its scale.The basic idea of the wavelet transform is to represent any arbitrary function as a superposition of a set of such wavelets or basis functions. These basis functions or baby wavelets are obtained from a single prototype wavelet called the mother wavelet, by dilations or contractions (scaling) and translations (shifts). They have advantages over traditional Fourier methods in analyzing physical situations where the signal contains discontinuities and sharp spikes. |
| Many new wavelet applications such as image compression, turbulence, human vision, radar, and earthquake prediction are developed in years. In wavelet transform the basis functions are wavelets. Wavelets tend to be irregular and symmetric. All wavelet functions, w(2kt - m), are derived from a single mother wavelet, w(t).we present an energy efficient wavelet image transform algorithm (EEWITA), consisting of techniques to eliminate computation of certain high-pass coefficients of an image. As shown by our experiments, the use of EEWITA can significantly reduce both (i) computation energy,by minimizing the computation needed to compress an image,and (ii) communication energy, consumed by the RF component of the mobile appliance, which is proportional to the number of bits transmitted. The reduction in energy is obtained with minimally perceptible loss in image quality. |
WAVELET IMAGE COMPRESSION
|
| JPEG image compression standard is in wide spread use today. |
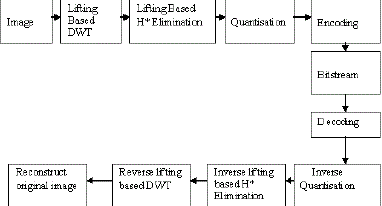 |
| JPEG uses the Discrete Cosine Transform (DCT) as the transform, applied to 8-by-8 blocks of image data. The newer standard JPEG2000 is based on the Wavelet Transform (WT). Wavelet Transform offers multi-resolution image analysis, which appears to be well matched to the low level characteristic of human vision.Joint Photographic Expert Group (JPEG) has developed a new wavelet-based image compression standard,commonly referred to as JPEG2000.Our preliminary study on wavelet-based image compression (using JPEG2000 ) shows that the wavelet transform step consumes more than 60 % of the CPU time during image compression process. By optimizing algorithmic features of the transform step,performance and energy requirements of the entire image compression process can be significantly improved. For this reason, we target the wavelet transform step to minimize the energy consumption. |
A) Wavelet Transform Overview
|
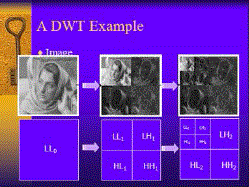
| The forward wavelet-based transform uses a 1-D subband decomposition process where a 1-D set of samples is converted into the low-pass subband (Li) and high-pass subband (Hi). The low-pass subband represents a downsampled low-resolution version of the original image. It used for computer and human vision, musical tone generation,FBI finger print compression. |
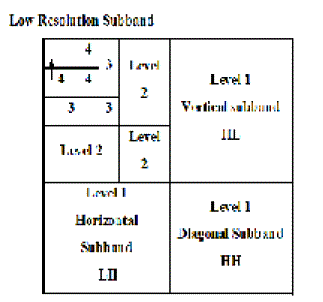 |
| The high-pass subband represents residual information of the original image, needed for the perfect reconstruction of the original image from the low-pass subband.The 2-D subband decomposition is just an extension of 1-D subband decomposition. The entire process is carried out by executing a 1-D subband decomposition twice, first in one direction (horizontal), then in the orthogonal (vertical) direction.For example, the low-pass subband (Li) resulting from the horizontal direction is further decomposed in the vertical direction, leading to LLi and LHi subbands. |
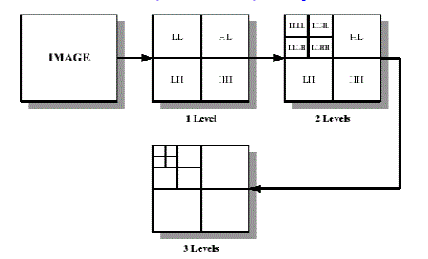 |
| Similarly, the highpass subband (Hi) is further decomposed into HLi and HHi. After one level of transform, the image can be further decomposed by applying the 2-D subband decomposition to the existing LLi subband. This iterative process results in multiple “transform levels”. For example the first level of transform results in LH1, HL1, and HH1, in addition to LL1, which is further decomposed into LH2, HL2, HH2, LL2 at the second level, and the information of LL2 is used for the third level transform. We refer to the subband LLi as a low-resolution subband and high-pass subbands LHi, HLi, HHi as horizontal, vertical, and diagonal subband respectively since they represent the horizontal, vertical, and diagonal residual information of the original image |
LIFTING SCHEME WAVELETS
|
 |
| Wavelet algorithms are recursive.The output of one step of the algorithm becomes the input for the next step. The Forward lifting scheme wavelet transform divides the data set being processed into an even half and odd half.Lifting scheme algorithms have the advantage that they do not require temporary arrays in the calculation steps,as is necessary for some versions of the Daubechies D4 Wavelet algorithm. The Predict step calculates the wavelet function in the wavelet transform.This is a high Pass filter.The update step calculates the scaling function,which results in a smoother version of the data. |
| This operation consists of three steps. |
| 1)First, the input signal x[n] is down sampled into the even position signal xe (n) and the odd position signal xo(n) , then modifying these values using alternating prediction and updating steps. |
| xe (n) = x [2n] and xo(n) = x [2n+1] |
| 2)A prediction step consists of predicting each odd sample as a linear combination of the even samples and subtracting it from the odd sample to form the prediction error. |
| 3)An update step consists of updating the even samples by adding them to a linear combination of the prediction error to form the updated sequence. The prediction and update may be evaluated in several steps until the forward transform is completed. |
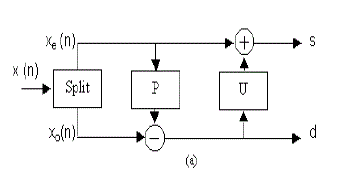 |
| The above diagram is Lifting scheme forward wavelet transform.The reverse Lifting used in inverse Lifting wavelet transform,this is below. |
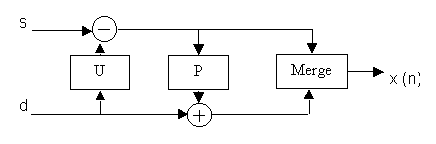 |
| The 9-7 and 5-3 Daubechies biorthogonal filters, were chosen as ideal for image compression. Both the biorthogonal 9- 7 and 5-3 filters were used in AWIC (Rushanan 1997). The detracting visual artifact at high compression rates using the longer filter is ringing, while the shorter filter produces staircasing. The design trade-off between these two filters is speed performance and quality performance. Visually, the level of ringing artifacts and staircasing artifacts appears to be nearly equivalent, dependent on subjective opinion. The peak-signal-to-noise ratio favors the ringing artifact over the staircasing. The Daubechies 5-tap/3-tap filter is used in forward wavelet transform and it has good localization and symmetric properties, which allows simple edge treatment, high-speed computation, and high quality compressed image. Daubechies 9-tap/5-tap filter is used for lifting based wavelet transform. |
A)Analysis of Energy Consumption
|
| By using Daubechies 5-tap/3-tap filter in the forward wavelet decomposition using the forward filter, 8 shift and 8 add operations are required to convert the sample image pixel into a low-pass coefficient. Similarly, high-pass decomposition requires 2 shift and 4 adds. Thus 8S + 8A units of computational load are required in a unit pixel of the low-pass decomposition and 2S + 4A units for the high-passes. Since all even-positioned image pixels are decomposed into the low-pass coefficients and odd-positioned image pixels are decomposed into the high-pass coefficients, the total computational load involved in horizontal decomposition is 1/2MN(10S+12A). The amount of computational load in the vertical decomposition is identical. |
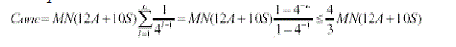 |
| we estimate the data-access load by counting the total number of memory accesses during the wavelet transform. At a transform level, each pixel is read twice and written twice. Data-access load : |
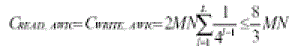 |
| The overall computation energy is computed as a weighted sum of the computational load and data-access load.We also estimate the communication energy by C*R, where C is the size of the compressed image (in bits) and R is the per bit transmission energy consumed by the RF transmitter. |
ENERGY EFFICIENT WAVELET IMAGE TRANSFORM ALGORITHM (EEWITA)
|
| we present EEWITA, a wavelet-based transform algorithm that aims at minimizing computation energy (by reducing the number of arithmetic operations and memory accesses) and communication energy (by reducing the number of transmitted bits). we can estimate the high-pass coefficients to be zeros (and hence avoid computing them) and incur minimal image quality loss. This approach has two main advantages. First, because the high-pass coefficients do not have to be computed, EEWITA helps to reduce the computation energy consumed during the wavelet image compression process by reducing the number of executed operations. Second, because the encoder and decoder are aware of the estimation technique, no information needs to be transmitted across the wireless channel, thereby reducing the communication energy required.Using the estimation technique presented, we have developed our EEWITA which consists of two techniques attempting to conserve energy by avoiding the computation and communication of highpass coefficients: |
| 1)Lifting Based HH Elimination |
| 2)Lifting Based H* elimination |
A)LIFTING BASED HH ELIMINATION:
|
| The first technique attempts to conserve energy by eliminating the least significant subband. Among the four subbands, we find that the diagonal subband (HHi) is least significant (Fig. 2), making it the best candidate for elimination during the wavelet transform step. We call this technique “HH elimination”. |
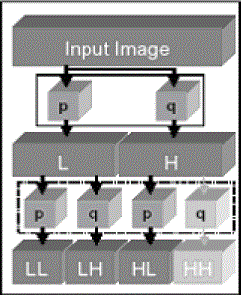
Lifting Based HH Elimination |
| Among the four subbands, we find that the diagonal subband (HHi) is least significant (Fig. 2), making it the best candidate for elimination during the wavelet transform step. We call this technique “HH elimination”. In the second scheme, only the most significant subband (low-resolution information, LLi) is kept and all high-pass subbands (LHi, HLi, and HHi) are removed. We call this “H* elimination”, because all high-pass subbands are eliminated in the transform step. |
1)Energy Efficiency of Elimination Techniques
|
| In the HH elimination technique, the computation load during the row transform is the same as with the AWIC algorithm. However, during the column transform of the high-pass subband resulting from the previous row transform, the high-pass subband (HH) is not computed.the results shows that this leads to a savings of 1/4MN(4A+2S) operation units of computational load (7.4 % compared to the AWIC algorithm). Therefore, the total computational load when using HH elimination is represented as: |
| Computational load : |
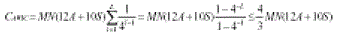 |
| Because the high-pass subband resulting from the row transform is still required to compute the HL subband during the column transform, we cannot save on “read” accesses using the HH elimination technique. However, we can save on a quarter of “write” operations (12.5 % savings) during the column transform since the results of HH subband are preassigned to zeros before the transform is computed. Thus, the total data-access load is given by: |
| Data-access load : |
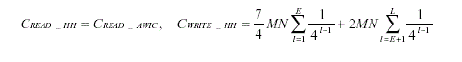 |
B) LIFTING BASED H* ELIMINATION:
|
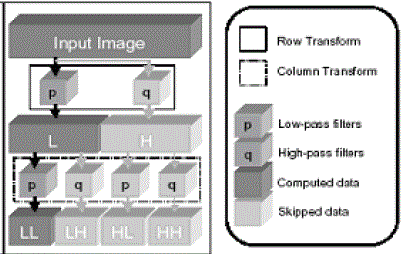
Lifting Based H* Elimination |
| HH elimination technique is applied, 25 % of the image data is removed leading to less information to be transmitted over the wireless channel. While the HH elimination technique reduces some computation loads during the transform steps by eliminating one out of every four subbands, the H* elimination technique targets more significant computation energy savings.In the H* elimination technique only the LL subband is generated and all highpass subbands are removed. Thus, only even-positioned pixels are processed in the row transform and fed to the subsequent column transform. Odd-positioned pixels are skipped, since these pixels represent all the high-pass coefficients (HL, HH). Similarly, at the column transform step, all odd-columned pixels are skipped and only even-columned low-passed pixels are processed. This leads to a savings of MN(6A+4S) operation units of computational load (over 47 % compared to the AWIC algorithm). Therefore, the total computational load when using H* elimination is represented as: |
| Computational load : |
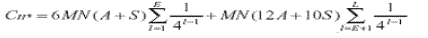 |
| H* elimination also reduces the data-access load .It reduce the number of “read” accesses by 25 %. Similarly, write operations are saved by 63 %. The total data-access load is given by: Data-access load : |
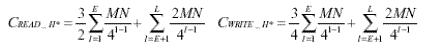 |
| The H* elimination technique can result in significant savings in communication energy since three out of four subbands are removed from the compressed result. |
RESULTS
|
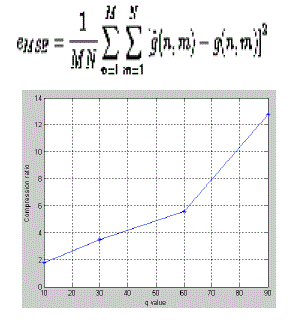
| Thus the lifting based Discrete wavelet transform have been developed for image compression.The quality of the image obtained increases with respect to compression ratio.Also larger the compression ratio,more the peak signal to noise ratio.The plots are shown below.Comparing restoration results requires a measure of image quality. Two commonly used measures are Mean-Squared Error and Peak Signal-to-Noise Ratio .The mean-squared error(MSE) between two images g(x,y) and g^(x,y) is: |
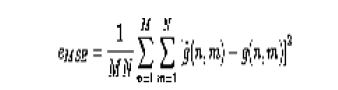 |
 |
| One problem with mean-squared error is that it depends strongly on the image intensity scaling. A mean-squared error of 100.0 for an 8-bit image (with pixel values in the range 0-255) looks dreadful; but a MSE of 100.0 for a 10-bit image (pixel values in [0,1023]) is barely noticeable. Peak Signal-to-Noise Ratio (PSNR) avoids this problem by scaling the MSE according to the image range: |
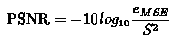 |
 |
| where S is the maximum pixel value. PSNR is measured in decibels (dB). The PSNR measure is also not ideal, but is in common use. Its main failing is that the signal strength is estimated as , rather than the actual signal strength for the image. PSNR is a good measure for comparing restoration results for the same image.MSE and PSNR provided in this paper were calculated after quantization (i.e. after converting floating-point pixel values to integer). |
CONCLUSION
|
| Future deployment of cellular multimedia data services will require very large amounts of data to be transmitted, creating tremendously high energy and bandwidth requirements that cannot be fulfilled by limited growth in battery technologies, or the projected growth in available cellular bandwidth. This paper presents a potential solution to the emerging problem, by developing an energy efficient image codec. By using this I can achive high image quality, and reduce energy during communication.So I can achive efficient bandwidth. Here I eliminate roundoff noise error by lifting scheme.In this paper JPEG 2000 offers numerous benefits over current compression methods, including the ability to do both lossless and lossy compression, the ability to obtain higher image quality and higher compression ratios, and ability to view the same file at multiple resolutions.In the future, we will extend our approach to other types of multimedia data like streaming video, as well as address other parameters of wireless data services like transmission latency, transmission robustness, and security. |
References
|
- J. Rushanan, “AWIC: Adaptive Wavelet Image Compress-ion for Still Image”, MTR-97B0000041, The MITRECorporation, Bedford, MA, September 1997.
- Chao-Tsung Huang, Po-Chih Tseng, Liang-Gee Chen,” Flipping structure: an efficient VLSI architecture forlifting-based discrete wavelet transform”, IEEE Transactions on Signal Processing, Volume 52, Issue 4, April 2004Page(s):1080 – 1089
- N. D. Zervas, et. al, “Evaluation of design alternatives for the 2-Ddiscrete wavelet transform,”IEEE Trans. Circuits Syst. Video Technol.ol.
- Bing-Fei Wu, Chung-Fu Lin,” A high- performance and memoryefficient pipeline architecture for the 5/3 and 9/7discrete wavelet transform of JPEG2000 codec”, IEEE Transactions on Circuits and Systems for Video Technology,Volume 15, Issue 12, Dec. 2005 Page(s):1615 – 1628
- Information Technology-JPEG 2000 Image Coding System, ISO/IEC. ISO/IEC 15 444-1,2000.
- H. Liao, M. Kr. Mandal, and B.F. Cockburn, :Efficient architecture for 1-D and 2-D lifting based wavelet transform,“IEEE Trans. Signal process.
|