Keywords
|
| FBMC, RRC, isotropic weighted Hermite, Fourier invariant signal, BT product, Interference plots |
I. INTRODUCTION
|
| Multicarrier modulation techniques has become the de facto choice for the current communication systems such as digital subscriber lines (DSL), wireless area network (WLAN) and long term evolution (LTE). The orthogonal frequency division multiplexing (OFDM) is one of the most commonly used multicarrier technique for high speed data transmission. But in some applications such as spectrum sensing and uplink of multiuser multicarrier systems [1], OFDM is not an effective solution. Filter bank based multicarrier techniques are (FBMC) alternative methods for OFDM system which have many advantages over OFDM such as lack of time and frequency guard bands which increases the bandwidth efficiency, reduces both inter symbol and inter carrier interferences, high flexibility to allocate group of subcarriers to different users, better spectral efficiency. The first multicarrier methods that were developed, prior to OFDM, were filter bank-based. Pioneering work on filter bank multicarrier communication techniques was done by Chang [2] and Saltzberg [3] in the mid 1960’s. Early works in FBMC are only based on multipath delay of the channel. But Le Floch [4] developed a prototype filter which is efficient for avoiding the effects caused by both multipath delay and Doppler effect of the channel. |
| FBMC techniques are better suited for systems with high mobility and Doppler effect. Different types of FBMC modulation techniques are present. In doubly dispersive channel filtered multitone modulation(FMT)[5] is preferred because both time and frequency dispersion not only affect the orthogonality among the subcarriers in time and frequency domain but also it affects the Nyquist condition of the received filter which leads to carrier and symbol interference. The essential requirements for an ISI and ICI free transmission are the orthogonality in time and frequency domain and good time frequency localization (TFL). The orthogonality among the subcarriers depends upon the Nyquist condition given by |
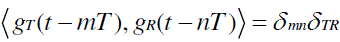 (1) (1) |
| where mn is the Kronecker delta function which is a two dimensional function |
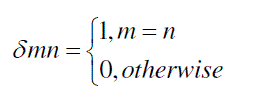 (2) (2) |
| The TFL depends on the Gabor uncertainty [6] principle which gives found the lower bound for the BT product |
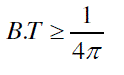 (3) (3) |
| where |
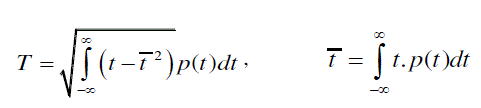 (4) (4) |
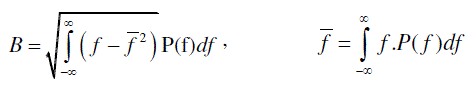 (5) (5) |
| The complete performance of an FBMC system depends upon the design of an appropriate prototype filter. The thrust of the paper is to present a comparison of three different prototype filters in terms of their BT product values and interference plots in time and frequency domain. Section II explains a basic FBMC system. The different prototype filters and performance evaluation methods and parameters/metrics are explained in section III and it is followed by simulation results in section IV and finally conclusion in section V. |
II. FBMC
|
| In filter bank based multicarrier communication, a set of parallel data symbols are transmitted through a bank of modulated filters and the synthesised transmitted signal is given by |
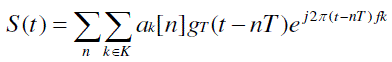 (6) (6) |
| where ak[n] are the subcarrier data symbols, k is the subcarrier index. For every n, S(t) is generated by adding a number of time-limited sub band signals , whose magnitude and phase are determined by the data symbols ak[n] .Separating different subcarriers (6) can be written as |
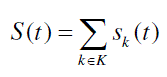 (7) (7) |
| where |
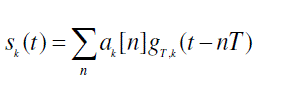 (8) (8) |
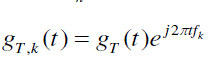 (9) (9) |
| The filtering operation applied to a sequence of impulses and the sub band filters are obtained by modulating the prototype filter.(8) The main difference between OFDM and FBMC lies in the choice of prototype filters .FBMC provide great flexibility in the design of prototype filter. |
III. DESIGN OF PROTOTYPE FILTERS
|
| In the FBMC modulation, the prototype filter completely defines the system. The choice of the prototype filter for the realization of the polyphase filter bank allows various tradeoffs among the number of subcarriers, the level of spectral containment, the complexity of implementation and signal latency to be made. In this paper root raised cosine (RRC), isotropic weighted Hermite and prototype filter based on Fourier invariant signal are compared. |
| A. Root Raised Cosine Filter(RRC) |
| The raised cosine filter satisfies the Nyquist condition completely. In RRC, the transmitter and receiver filters are jointly design for zero ISI. Hence if ( ) T G f is the frequency response of the transmitter and ( ) R G f is the frequency response of the receive filter, then the product ( ). ( ) T R G f G f is designed to yield zero ISI ie |
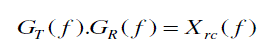 (10) (10) |
| where ( ) rc X f has a raised cosine frequency response characteristic, which is defined as |
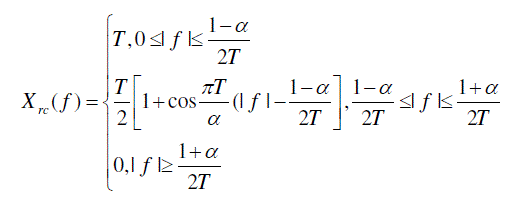 (11) (11) |
| where α is the roll off factor and 1/T is the symbol rate. The BT product values of RRC for different values of α are shown in table I. Table I reveals that RRC with α=1have minimum BT product .The interference plots of RRC with α=1 in both time and frequency domain is shown in Fig.1. From this it is clear that the interference caused in both time and frequency domain are different. The reason behind this is that RRC does not have same pulse shape in time and frequency domain so it is not an optimal choice for avoiding both multipath delay and Doppler effect caused by the channel. |
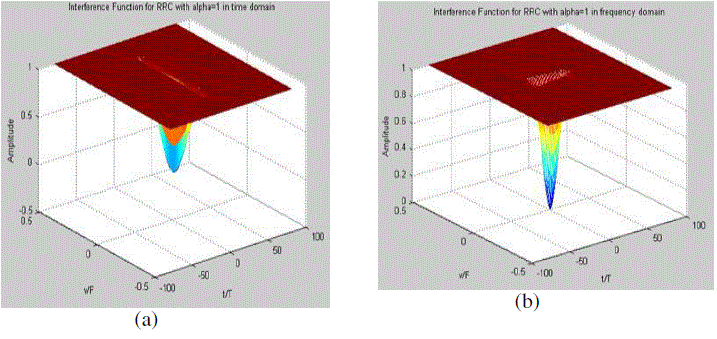
Figure 1: Interference plots of RRC in time and frequency domain with α=1 |
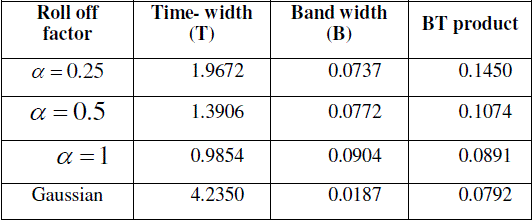
TABLE I: BT product values for RRC for different values of α |
| B. Isotropic Weighted Hermite Pulse |
| Isotropic means the pulse have similar shape in time and frequency domain.For doubly dispersive channel the orthogonality condition can be best explained through ambiguity function which is a two dimensional function of time delay τ and Doppler frequency υ given by |
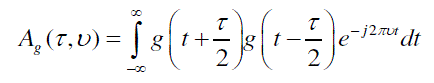 (12) (12) |
| From (1) |
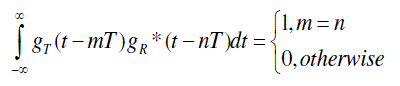 (13) (13) |
| From (9) |
| The ambiguity function is |
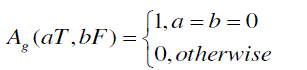 (15) (15) |
| This is the generalized Nyquist criteria to avoid the effects of channel impairments in both time and frequency domain. The Hass and Belfore [7] suggested a design procedure to produce isotropic filter from weighted Hermite pulses. The Hermite pulses are generally called root nyquist self transform pulses, self transform because the pulse have same shape in time and frequency domain and root nyquist because the square of the pulse produces a Nyquist pulse. Haas and Belfore generates an isotropic filter according to the equation |
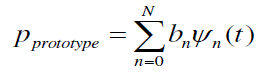 (16) (16) |
 |
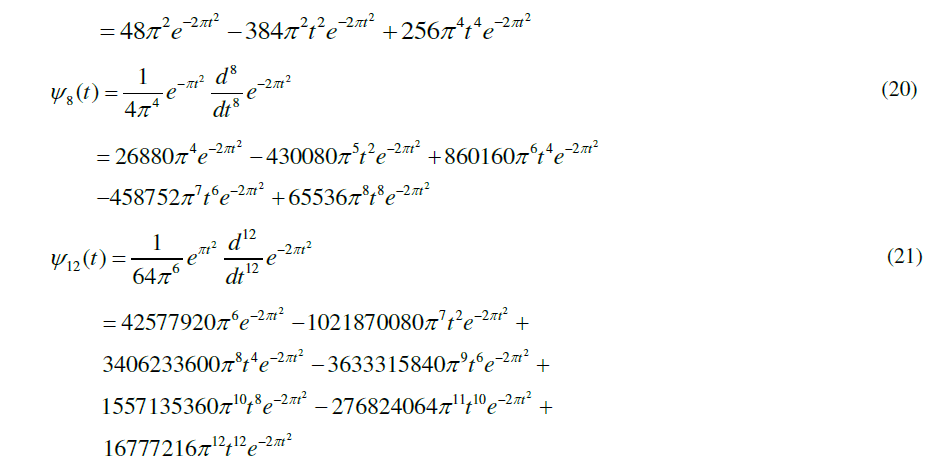 |
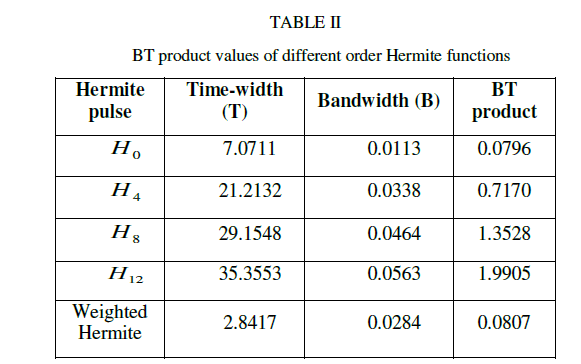
| From the above equations it is clear that the Hermite pulses are various functions of t multiplied by Gaussian function. Hence by equation (16) prototype p is an isotropic filter for any values of n b .But the prototype filter should satisfy the condition (15) for ISI and ICI free transmission. The weight vector 1 2 [ , ,...... ] N b b b b is calculated so that the resultant weighted Hermite pulse satisfies the constraint (15). The optimum pulse should have minimum BT product.Since Gaussian pulse have minimum BT product, strong weight should be given to the first Hermite. The BT product values of different order Hermite pulses and that of the resultant weighted Hermite pulse is given table II |
 |
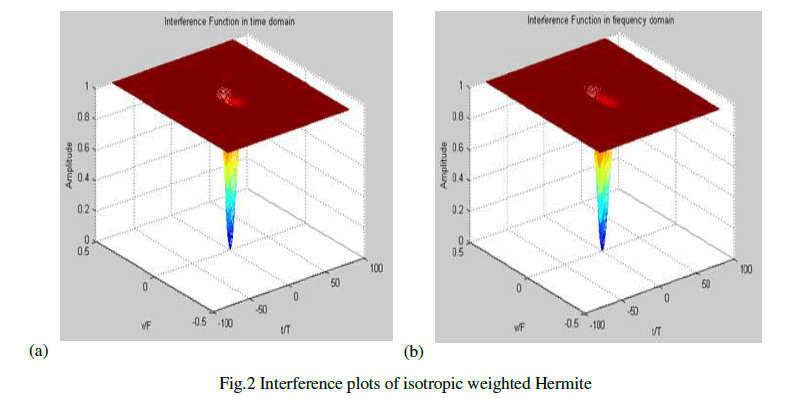
| The interference plots the optimum pulse shape in time and frequency domain is shown in Fig.2 which reveals that the interference caused in both time and frequency domain are same hence it is well suitable for avoiding both multipath delay and Doppler effect .Fig.2(a) gives the interference in time domain and Fig.2(b) gives the interference in frequency domain. |
 |
| C. Fourier Invariant signal |
| Maja Temerinac-Ott and Miodrag Temerinac[8] suggested a class of signals which maintain similar pulse shape in time and frequency domain and also have equal timewidth and bandwidth value hence it can be used as a substitute for isotropic weighted Hermite in doubly dispersive channel. The Fourier transform maps a time signal x(t) into the frequency function X(f) is given by |
 |
| There is a very interesting aspect of the Fourier transform, the notion of its eigen functions. If x(t) is a non zero function which has same pulse shape in time and frequency domain then |
 |
| The CDFT eigenvector is a vector which satisfies |
 |
| where λ has four possible values:±1 and ±j. The eigenvectors are even symmetrical for λ=1and odd symmetrical for λ=j.For discrete Fourier invariant signals (dφ -signals) the case λ= 1 is assumed. The condition of the discrete Fourierinvariant function can be expressed in a form using the real-valued transform matrix R of size K x K |
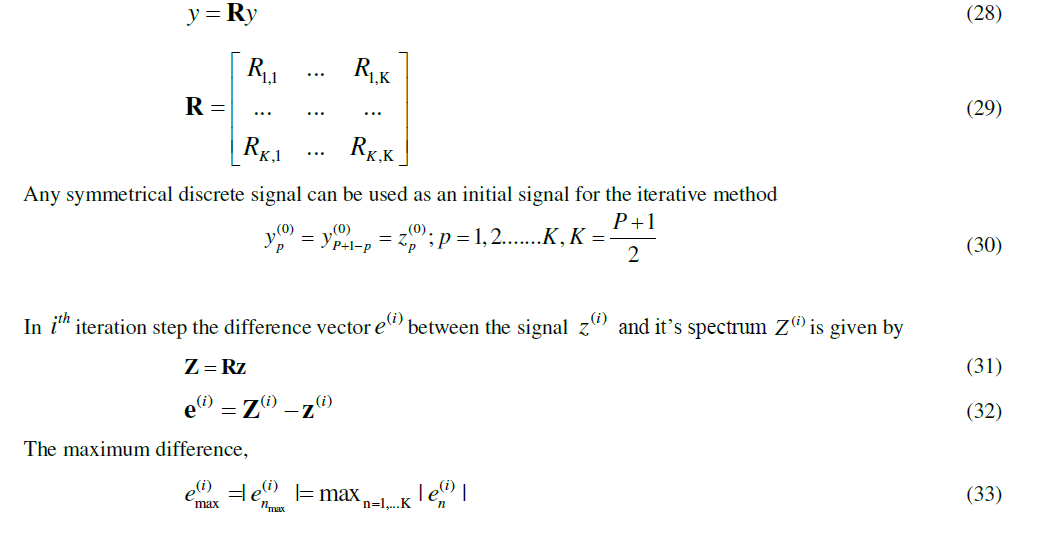 |
 |
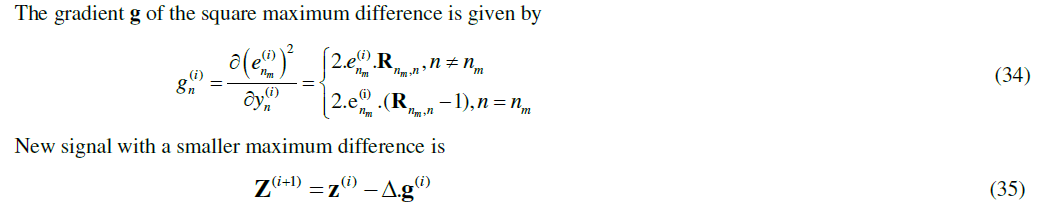 |
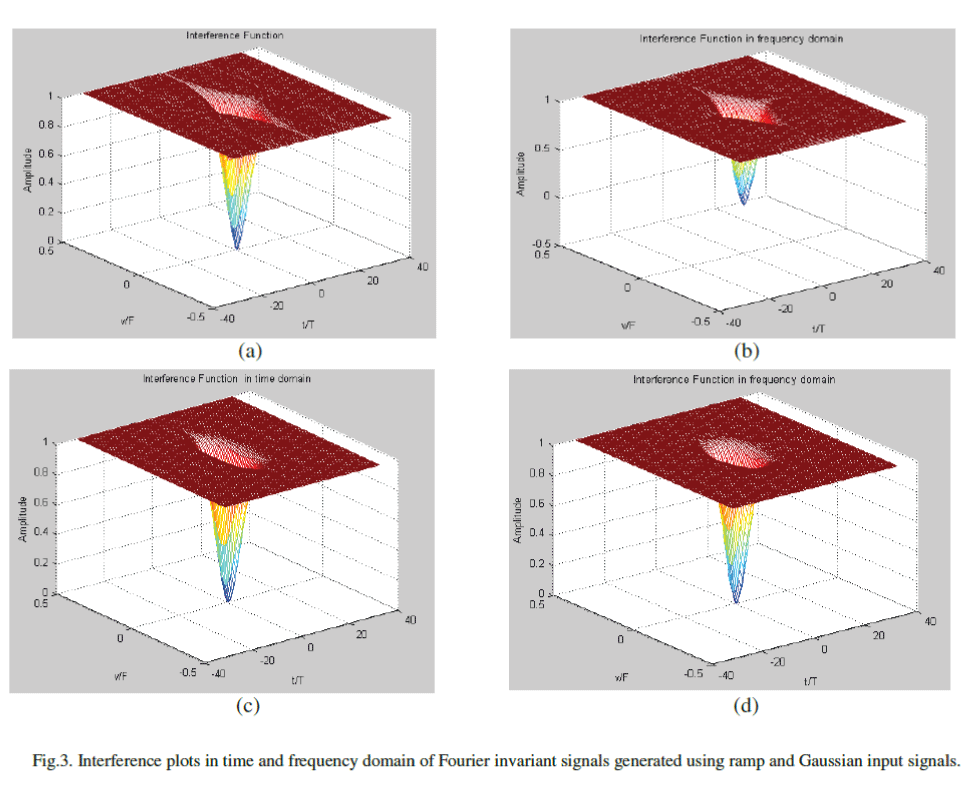
| The convergence of the iteration procedure depends upon the value of the gain constant Δ which is limited by the stability condition of the iteration. The resultant dïÿý signal is not a unique solution as it depends on the initial signal at the start of the iterations. The interference plots of Fourier invariant signal generated using a ramp and a Gaussian input signal is shown in Fig 3.Fig 3(a) and 3(b) shows the interference plots in time and frequency domain for ramp input. Fig 3(c) and 3(d) shows the interference plots in time and frequency domain for a Gaussian input. The interference caused in time and frequency domain is almost same, but the Fourier invariant signal using the Gaussian input causes minimum interference. |
| D. Performance evaluation using image transmission and parameters/metrics |
| The source data to the filter bank is taken from an 8 bit greyscale bitmap image. The four performance metrics which are used to evaluate the quality of received image are quality index, peak signal to noise ratio (PSNR), signal to noise ratio (SNR) and root mean square error (RMSE) |
| 1) Quality Index |
| Let I and H be the original/transmitted and reconstructed image matrices with P rows and N columns then |
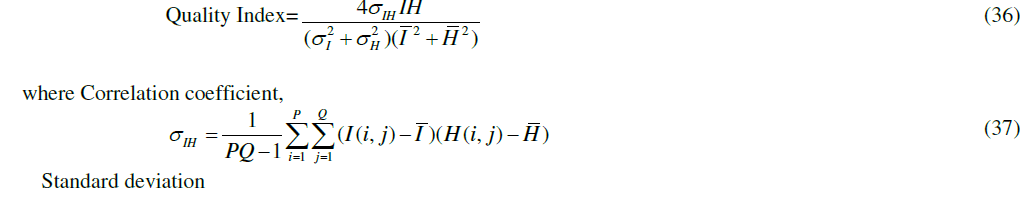 |
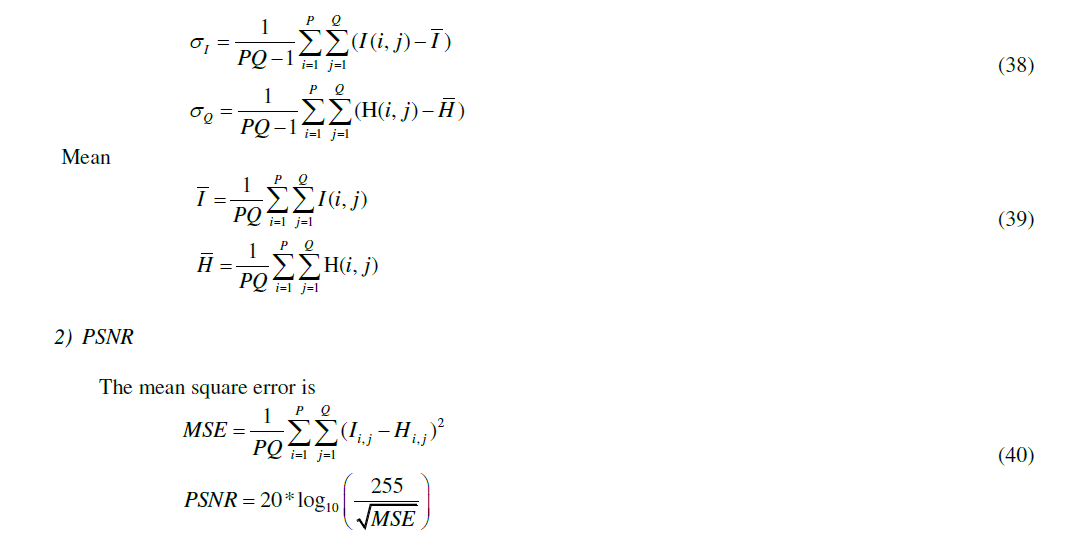 |
IV. SIMULATION RESULTS
|
| Pixel values of an 8-bit bitmap image are used as the source data and the performance metrics of the three filters are evaluated by using the noisy received image are tabulated in table III. The BT product values of prototype filters are given in table IV. The weighted Hermite have minimum BT product compared with the other two. |
 |
V. CONCLUSION
|
| In this paper the performance of three different prototype filters in a digital FBMC system is evaluated. The root raised cosine filter is an effective solution for avoiding either multipath delay or Doppler effect of the channel. However it is not effective for doubly dispersive channel since the orthogonality in time domain doesn’t leads to orthogonality in frequency domain. Both isotropic weighted Hermite and prototype filter based on Fourier invariant signal have same pulse shape in time and frequency domain and hence both are well suitable for doubly dispersive channels. The prototype filter based on Fourier invariant signal is a new concept and it can be used as a substitute for weighted Hermite. The three prototype filters are compared based on the interference plots in time and frequency domain. Of the three, the isotropic weighted Hermite cause minimum interference. The interference caused by the prototype filter based on Fourier invariant signal depends upon the type of input signal used in the iteration method. For a Gaussian input, the interference caused is minimum compared to ramp input. By comparing the BT product values of three prototype filter, isotropic weighted Hermite have minimum BT product. A further investigation into the design of prototype filter using Fourier invariant signal may lead to a better prototype filter to be used in FBMC systems. |
References
|
- B. Farhang-Boroujeny, “OFDM versus filter bank multicarrier,” IEEE Signal Process.Mag., vol. 28, no. 3, pp. 92–112, May 2011.
- R. Chang, “High-speed multichannel data transmission with band limited orthogonal signals," Bell Sys. Tech. J., vol. 45, pp. 1775-1796,Dec. 1966.
- B. Saltzberg, “Performance of an efficient parallel data transmission system,’’ IEEE Trans. on Comm. Tech., vol. 15, no. 6, pp. 805-811,Dec. 1967.
- B. Le Floch, M. Alard, and C. Berrou, “Coded orthogonal frequency division multiplex,” Proceedings of the IEEE, vol. 83, no. 6, pp. 982–996,1995.
- G. Cherubini, E. Eleftheriou, S. Olcer, “Filtered multitone modulation for VDSL,” in Proc. IEEE Globecom’99, vol. 2, pp. 1139-1144, 1999
- D. Gabor, “Theory of communication. Part 1: The analysis of information,”Elect. Eng.—Part III: Radio Commun. Eng. J. Inst., vol. 93, no.26,pp. 429–441, Nov. 1946.
- R. Haas, and J.-C. Belfiore, “A time-frequency well-localized pulse for multiple carrier transmission,” Wireless Personal Communications,vol.5, pp. 1-18, 1997.
- Maja Temerinac-Ott, and Miodrag Temerinac, “Discrete Fourier-Invariant Signals: Design and Application”, IEEE transactions on Signalprocessing, vol. 60, no. 3, pp. 1108-1120, March 2012.
- C.Candan, “On the eigenstructure of DFT matrices DSP education],” IEEE Signal Process. Mag.,vol.28,no.2,pp. 105-108,Mar.2011.
|