Performance of Attribute Charts and Fuzzy
Control Chart for Variable Data

A.Saravanan; Dr. V.Alamelumangai

Performance of Attribute Charts and Fuzzy Control Chart for Variable Data

A.Saravanan¹ , Dr. V.Alamelumangai²

Assistant professor, Department of Instrumentation Technology, M.S.R.I.T, Bangalore, India
Professor, Department of Electronics and Instrumentation Engineering, Annamalai University, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The Quality has evolved through a number of stages such as inspection, quality control, quality assurance, and total quality control and the results produced by the above stages are used to control and improve the manufacturing process. Statistical process control (SPC) is a powerful collection of problem solving tools useful in achieving process stability and improving capability through the reduction of variability.SPC can be applied to any process. A control chart is a statistical tool used to distinguish between variations in a process resulting from common causes and variation resulting from special causes. One of the basic control charts is p -chart. For the quality related characteristics such as characteristics for appearance, softness, color, taste, etc., attribute control charts such as p-chart, c -chart are used to monitor the production process. The p -chart is used to monitor the process based upon the fraction In classical p -charts, each item classifies as either "nonconforming" or "conforming" to the specification with respect to the quality characteristic. Another attribute chart is CUSUM (cumulative sum) chart which can be used during smaller shifts occur. For many problems control limits could not be so precise .uncertainty comes from the measurement system including operators, environmental conditions etc .In this situation fuzzy set theory is a useful tool to handle this uncertainty Fuzzy control limits provide a more accurate and flexible evaluation. In this paper the attributes charts like p- chart and CUSUM chart and also fuzzy α cut control chart for standard deviation are constructed for the variable data to improve the process

Keywords

Attribute charts, p -chart, CUSUM, fuzzy α cut and α –level fuzzy mid range

I. INTRODUCTION

Statistical Process Control (SPC) is used to monitor the process stability which ensures the predictability of the process. The power of control charts lies in their ability to detect process shift and to identify abnormal conditions in the process. In 1924, Walter Shewhart designed the first control chart. According to him, if w be a sample statistic that measures some quality characteristic of interest the mean of w is w, and the standard deviation of w is w, then the center line (CL), the upper control limit (UCL) and the lower control limit (LCL) are defined as

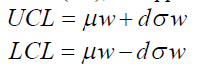where d is the “distance” of the control limits from the center line, expressed in standard deviation units. A single measurable quality characteristic such as dimension, weight or volume is called a variable. In such cases, control charts for variables are used to monitor the process. These include the X-chart for controlling the process average and the R -chart (or S -chart) for controlling the process variability. For the quality-related characteristics such as characteristics for appearance, softness, color, taste, etc., attribute control charts such as p-chart, c-chart are used to monitor the production process. Sometimes the product units are classified as either "conforming" or "nonconforming", depending upon whether or not product units meet some specifications. The p -chart is used to monitor the process based upon the fraction of non conforming units.

Many quality characteristics cannot be conveniently represented numerically. In such cases we usually classify each item inspected as either conforming or non conforming to the specifications on that quality characteristics. Numerical

Example:

In practice, one may classify each item in more than two categories such as "bad", "medium", "good", and "excellent”. On a production line, a visual control of the particular product might have the following assessment possibilities

1. "Reject" if the product does not work;.

2. "Poor quality" if the product works but has some defects;

3. "Medium quality" if the product works and has no defects, but it has some aesthetic flaws;

4. "Good quality" if the product works and has no defects, but has few aesthetic flaws;

5. "Excellent quality" if the product works and has neither defects nor aesthetic flaws of any kind.

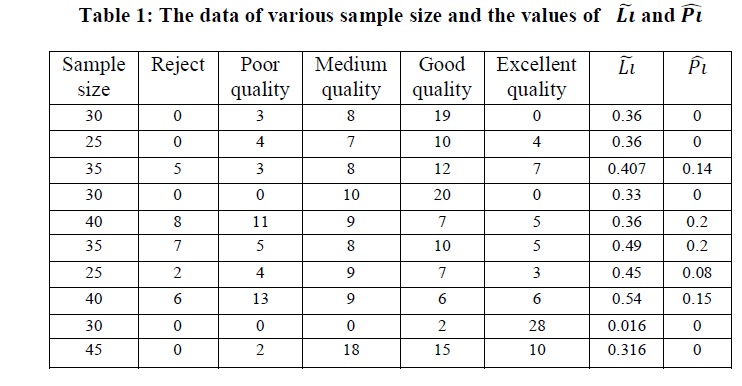
To monitor the quality of this product, 10 samples of different sizes are selected. The degrees of membership for the above assessment are taken as 1, 0.75, 0.5, 0.25 and 0 respectively. The data with and piˆ are given in Table –1.

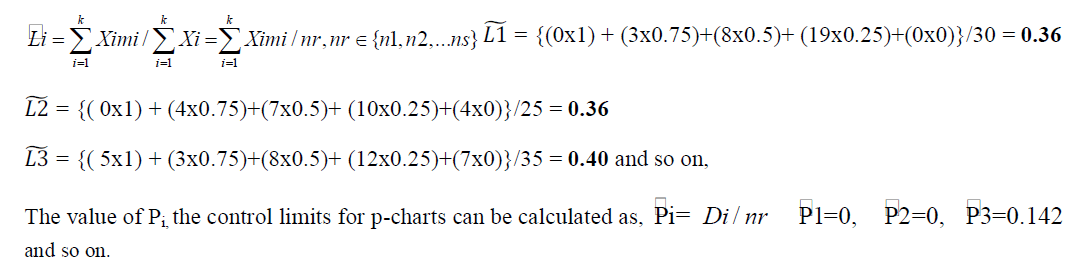For sample 1:

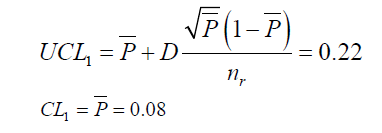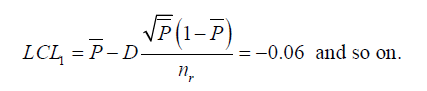The chart given below depicts the conventional p – chart for 10 samples

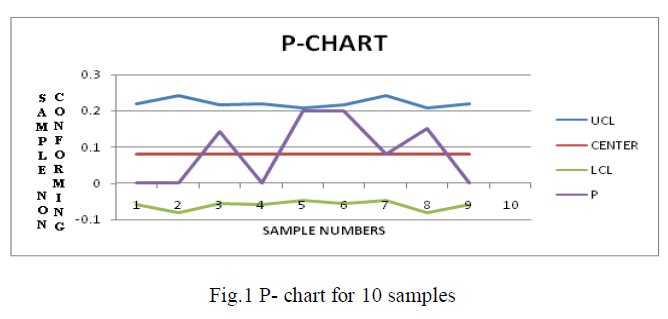In fig.1 out of control signal is not seen corresponding to the 10 samples. So the process is under control

II. CUSUM CHART

The cusum chart directly incorporates all the information in the sequence of sample values by plotting the cumulative sums of the deviations of the sample values from a target value. For example, suppose that samples of size n 1 are connected, and j x is the average of the jth sample. Then if 0 is the target for the process mean, the cumulative sum control chart is formed by plotting the quantity

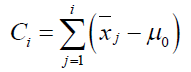Against the sample i. i C is called the cumulative sum up to and including the ith sample. Because they combine information from several samples, cumulative sum charts are more effective than Shewhart charts for detecting small process shifts. Cumulative sum control charts were first proposed by Page (1954) and have been studied by many authors; in particular, see Ewan (1963), Page (1961), Gan (1991), Lucas (1976), Hawkins (1981) (1993a), and Woodall and Adams (1993). In this section we concentrate on the cumulative sum chart for the process mean. It is possible to devise cumulative sum procedures for other variables, such as Poisson and binomial variables for modeling nonconformities and process fallout. We will show subsequently how the cusum can be used for monitoring process variability.

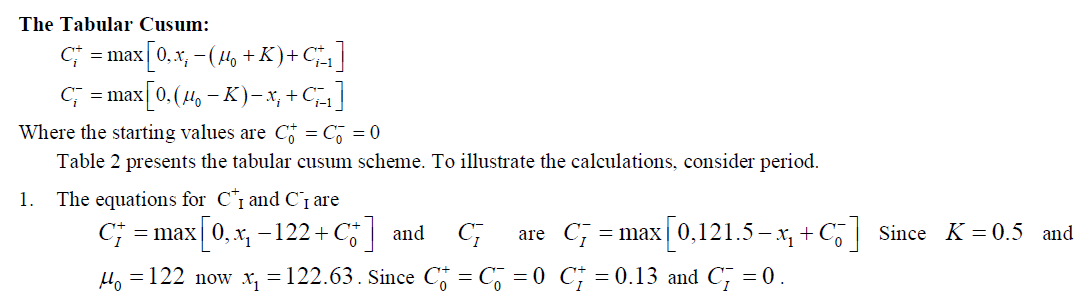III. RESULT

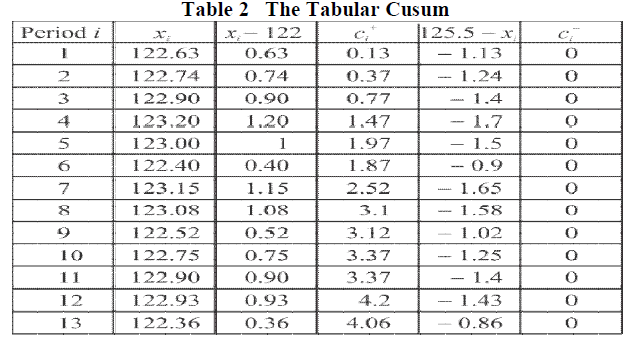
The cusum calculations in table 2 show that the upper side cusum at period 15 is c+15=5.76 Since this is the first period at which c+i > H=5we would conclude that the process is out of control at that point

IV. FUZZY X CONTROL CHART BASED ON STANDARD DEVIATION

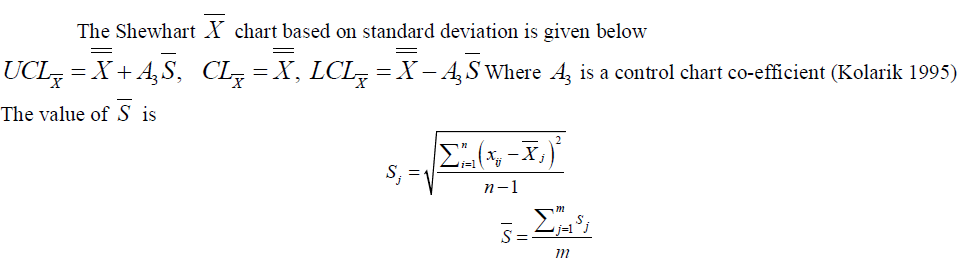Where j S is the standard deviation of sample j and S is the average of ' j S s .

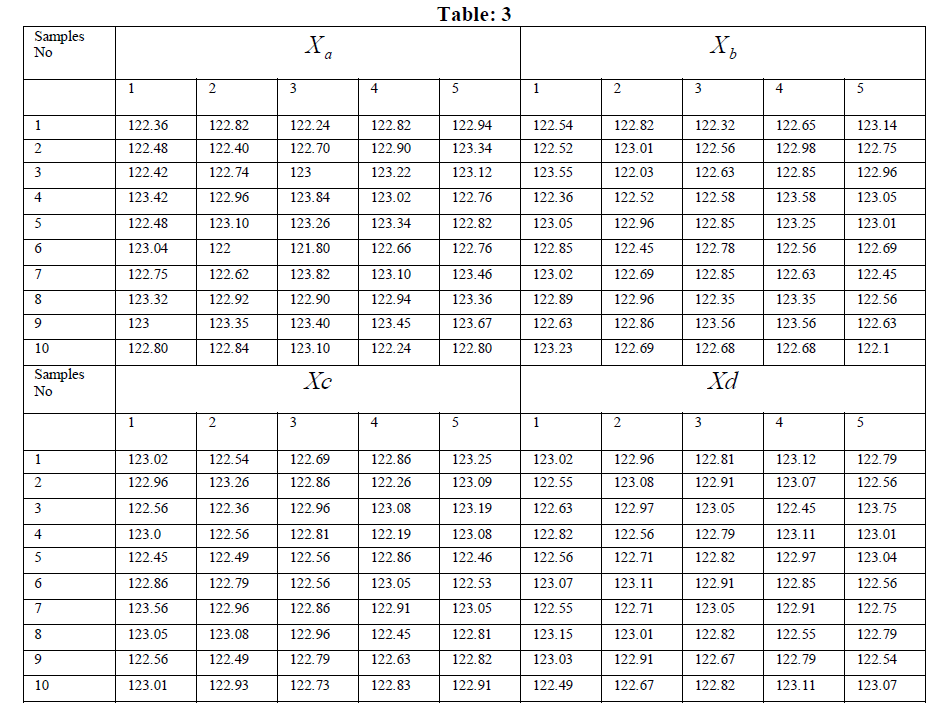
Application: Different Observation data have been considered with 10 samples. Fuzzy control limits are calculated according to the procedures. For n = 5,A2 = 0.577 Where A2 is obtained from the coefficients table for variable control charts

V. FUZZY X CONTROL CHART BASED ON STANDARD DEVIATION

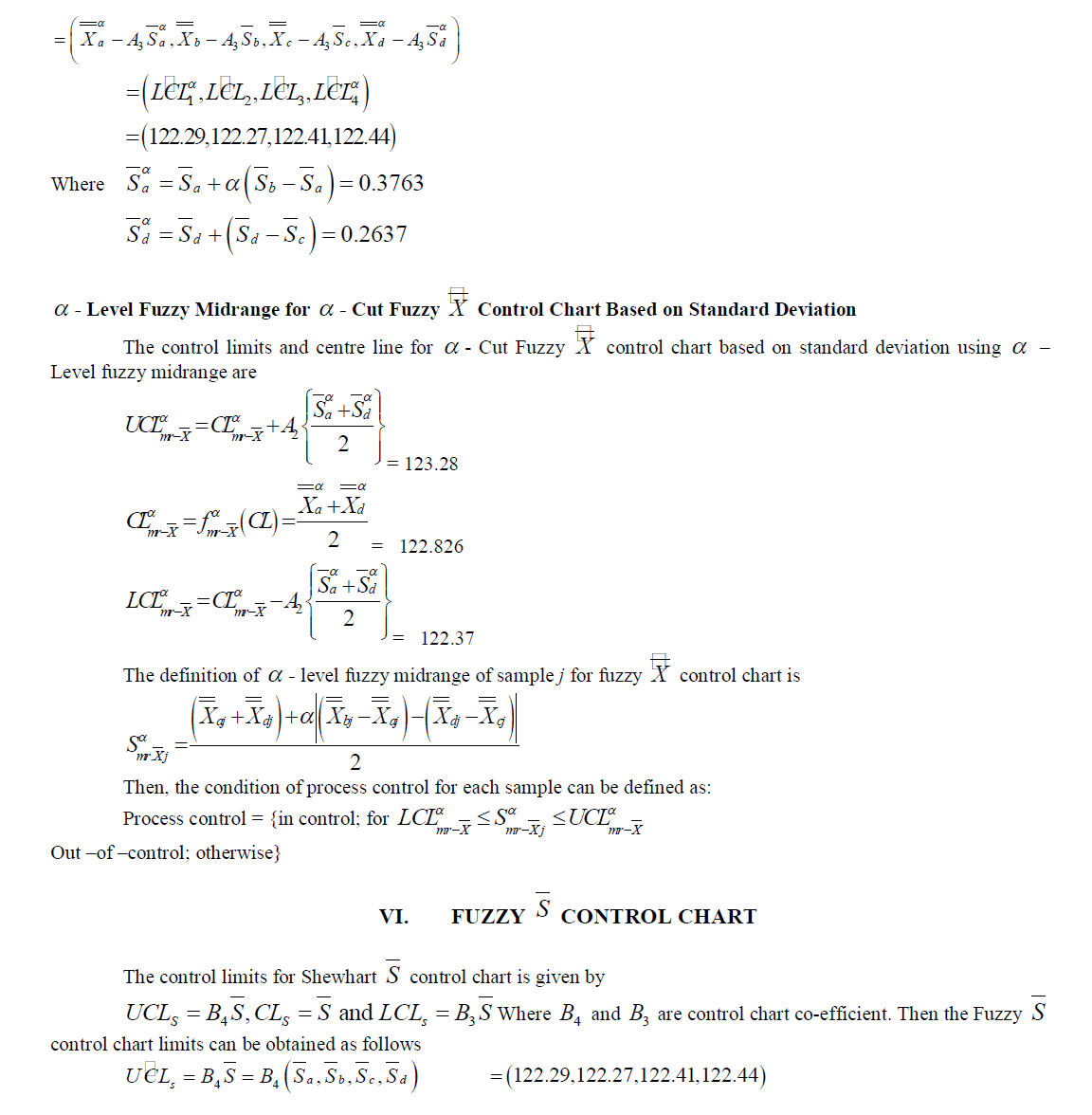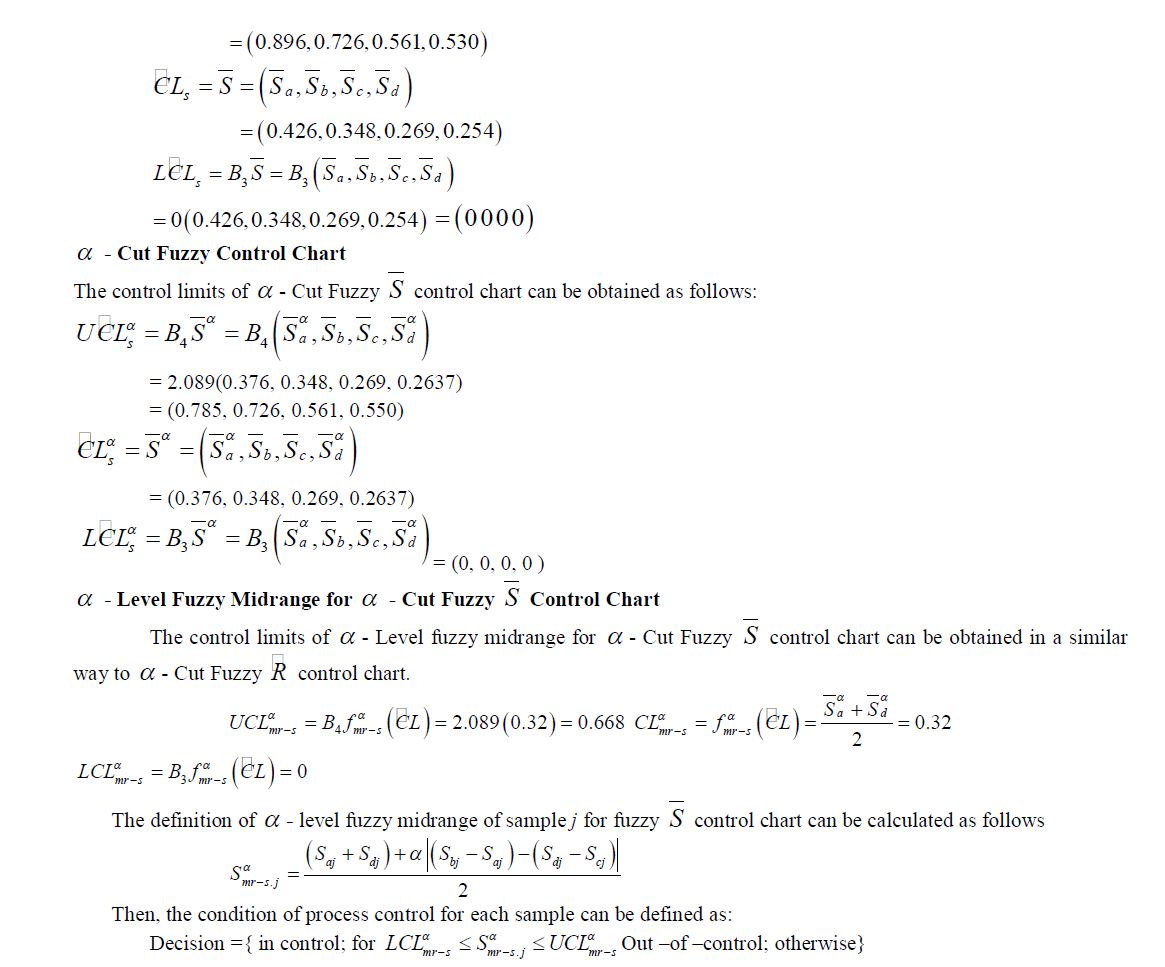VII. RESULT AND CONCLUSION

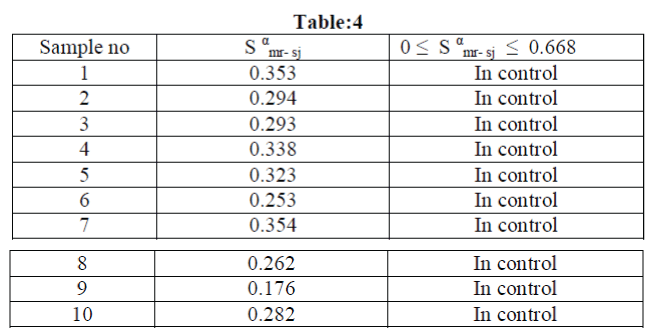
From Table 4 it is found that the process is under control with respect to S α mr- sj for each sample. So these control limits can be used to control the production process. Since the plotted values are close to the control limits, Fuzzy control limits can provide more flexibility for controlling a process.Control charts have an efficient usage field to keep the process under control. In this investigation control chart and fuzzy logic are tried to combine. Construction of fuzzy control chart has some advantages and disadvantages. The major contribution of fuzzy set theory is its capability of representing vague data. With the help of the fuzzy set theory, flexibility of the system is improved. The main difficulty of constructing fuzzy control chart is selecting suitable membership function of linguistic variables. The assignment of membership function to each linguistic variable is not easy for process and quality engineers. The shape of membership function should be based on system behavior and user’s preferences and also increasing and decreasing number of linguistic variables affect the performance of fuzzy control chart.

References

Ryan, T. (1989), Statistical Methods for Quality Improvement, New York: John Wiley & sons

Wang, J.H and Raz, T. (1990a) “On the construction of control charts using Linguistic Variables”, Intelligent Journal of Production Research 28, pp. 477-487

Wetherill,G.B And D.W.Brown(1991).”Statistical Process Control: Theory and Practice”, chapman and hall ,New York

Wheeler, D J & Chambers, D S (1992), Understanding Statistical Process Control ISBN 0-945320-13-2

El – Shal, S. M., Morris A. S. (2000) “A fuzzy rule -based algorithm to improve the performance of statistical process control in qualitySystems”, Journal of Intelligent Fuzzy Systems, 9, pp. 207– 223

Rowlands, H and Wang, L.R, (2000) “An approach of fuzzy logic evaluation and control in SPC”, Quality Reliability Engineering Intelligent ,16, pp. 91-98

Basher,I.A&Hajmeer.M(2000).’Artificial neural ntworks:fundamentals,computing,design and application’ Journal of microbiological methods 43,3-31

Gulbay, M., C. Kahraman and D. Ruan, (2004) “alpha - cut fuzzy control charts for linguistic data”, International Journal of IntelligentSystems. 19, pp. 1173-1196.

Gulbay, M and Kahraman, C. (2006) “Development of fuzzy process control charts and fuzzy unnatural pattern analysis”, Computational Statistics andData Analysis 51, pp. 434-451.

Gulbay, M and Kahraman, C. (2006) “An alternative approach to fuzzy control charts: direct fuzzy approach” Information Sciences, 77(6), pp.1463-1480

Pandurangan A and Varadharajan.R (2011), “Fuzzy Multinomial Control Chart with Variable Sample Size”, International Journal of EngineeringScience and technology, 3(9), pp. 6984– 6991.

Pandurangan A and Varadharajan.R (2011), “Construction of - Cut Fuzzy Control Charts Using Fuzzy Trapezoidal Number”, InternationalJournal of Research and Reviews forApplied Sciences, 9(1), pp. 100–111.

Nelson, L. (1984), "The Shewhart Control Chart -Tests for Special Causes," Journal of Quality Technology, 15, 237 -239.