Keywords
|
| Micro diversity, MMSE, ZF, outage probability, optimum combining, zero-forcing, Network MIMO |
I.INTRODUCTION
|
| With the increase in demand for the wireless systems, the performance enhancement of the systems has become a very important criterion. This need for performance increase by increased coverage and speed of transmission the MIMO systems have become very popular in today research developments. MIMO systems have fulfilled the needs of the technological development like wide coverage, high throughput and reliability of the services. |
| Since the MIMO fulfilled the present day technology needs, it has become very popular these days. Communication in wireless channels always comes in pair with the multipath fading. Multipath is the arrival of the multiple copies of the transmitted signal at the receiver through different angles and/or differing time delays and/or differing frequencies. MIMO offers significant increase in the data through put and link range without additional bandwidth or transmit power. Space diversity techniques have become very popular since last decade. This space diversity has provided increased efficiency of the communication systems by decoupling users through channel aware signal processing techniques. The adaptive equalization techniques have further helped to compensate the time dispersion in the channel. Much research has been done on the various processing techniques. Due to the simplicity the linear equalization techniques have attracted a lot of the researchers for communication signal processing. Two key equalization techniques include: MMSE (Minimum mean square error) and ZF (Zero forcing) techniques [2]. Though they are not optimum in performance they satisfy other criterions such as reduced mean square error (MMSE) and also interference eliminated (ZF). So far, a rich literature is available over the performance of ZF and MMSE for micro diversity systems, where there is a communication between co-located diversity antenna at the base station and the distributed users [3],[4],[7]. But not much research has been done on macro diversity systems where both transmit and receive antennas are widely separated. They occur naturally in network MIMO systems [9], [10] and collaborative MIMO systems [11, p.69] and [12]. |
| But the reason for lack of much research in the macrodiversity phenomenon can be attributed to complexity of the channel matrix [13]. In microdiversity Wishart form is used in classical models and Kronecker correlation matrices. However Wishart form is not followed in the macrodiversity thus making the analytical work extremely difficult. Hence only few results are available in macrodiversity case. The complexity in analysis is clearly evident in dual user scenario [14]. In this paper, ZF and MMSE equalization techniques are implemented over macro diversity case and their performances are compared for flat Rayleigh Frequency selective fading channel for different modulation schemes. BPSK, QPSK and QAM are simulated and compared for the above mentioned scenario. |
II. LITERATURE REVIEW
|
| J. H. Winters, J. Salz, and R. D. Gitlin, et al, , showed that a significant increase in system capacity can be achieved by the use of spatial diversity (multiple antennas), and optimum combining, for a broad class of interference-dominated wireless systems including mobile, personal communications, and wireless PBX/LAN networks. |
| M. K. Karakayali, G. J. Foschini, and R. A. Valenzuela, et al, (2006) proposed a method by considering network coordination as a means to provide spectrally efficient communications in cellular downlink systems. |
| L. Xiao, L. Dai, H. Zhuang, S. Zhou, and Y. Yao, investigated the information-theoretic capacity of DAS based on the channel model considering path loss, log-normal shadowing fading and Rayleigh fading |
| D. A. Basnayaka, “Macrodiversity MIMO Transceivers,” Ph.D. thesis, Dept. of Electrical and Computer Engineering, University of Canterbury, Jun. 2012. |
| P. J. Smith and D. A. Basnayaka, “Multiuser scheduling for radio resource allocation,” US provisional patent application 61/648505, filed May 17, 2012 |
III. SYSTEM MODEL AND ASSUMPTIONS
|
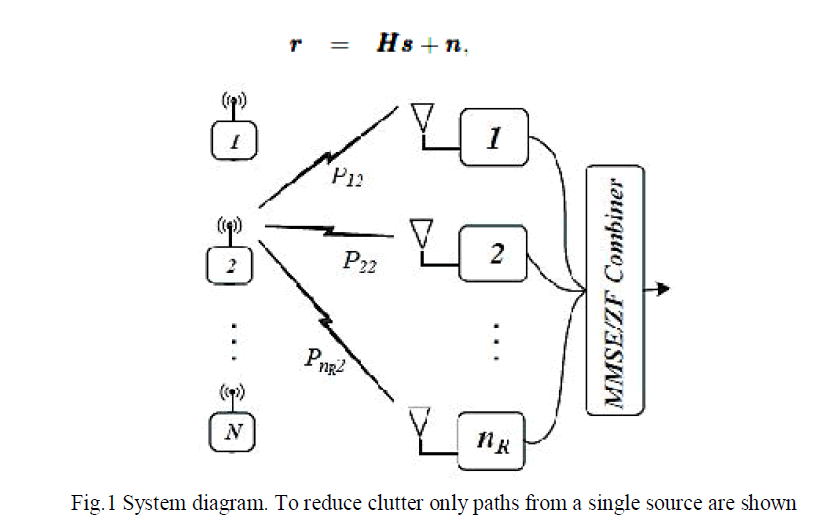
| In this section, we present the generic system model which is considered throughout this paper. The multiuser MIMO system investigated in this paper consists of N distributed single antenna users communicating with nR distributed receive antennas in an independent flat Rayleigh fading environment. The ïÿýïÿýïÿýïÿýïÿýïÿý×ïÿýïÿý receive vector is given by |
 |
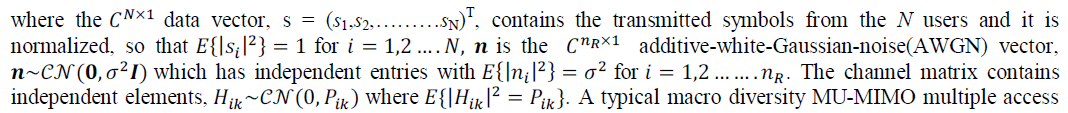 |
| channel (MAC) is shown in Fig.2, where it is clear that the geographical spread of users and antennas creates a channel matrix H, which has independent entries with difference Pik values. We define the CnRxN matrix, P= {Pik}, which holds the average link powers due to shadowing, path fading, etc. |
 |
| 3.2 High SNR Approximations: |
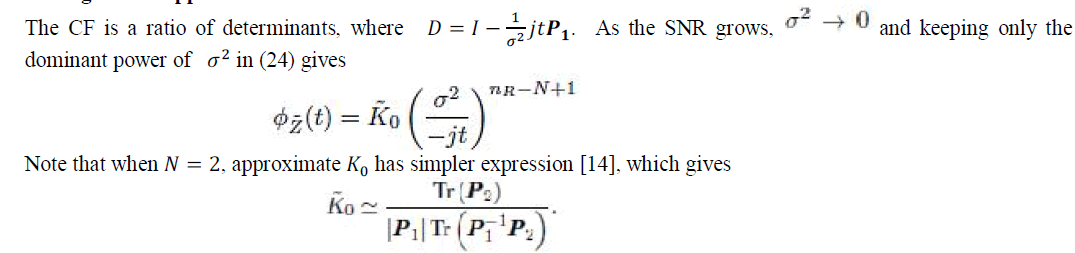 |
| The high SNR SER approximation in has the useful property that all the dependence on P is encapsulated in the K0 metric. This feature has implications for systems where only long-terms CSI is available for scheduling. Here, K0 can be used as a scheduling metric as it is a one-to-one function of the approximate SER. Such situations include systems with rapidly changing channels, systems where CSI exchange is too expensive and systems with large numbers of sources and/or receivers. In all these cases, long term CSI based scheduling may be preferable due to the overheads, delays and errors implicit in obtaining instantaneous CSI. |
V.MMSE ANALYSIS
|
| 4.1 CDF Approximations: |
| In this section, we derive the approximate CDF of the output SINR of an MMSE receiver and a high SNR approximation to the SER. Let Z be the output SINR of an MMSE receiver given by. Following the same procedure as in the ZF analysis, the CF of Z is |
 |
| In contrast to ZF, where the ZF SNR is a generalized mixture of L exponentials, this equation can be identified as a generalized mixture of nR ≥ L exponentials. Since the MMSE SINR has more mixing parameters (nR rather than L) it might be expected that these increased degrees of freedom will result in a better approximation. Alternatively, the more concise ZF result, which provides a lower bound on the MMSE performance, can be used to provide a simpler expression for use in system design and understanding. |
VI.SIMULATION AND NUMERCAL RESULTS
|
| In this section, we simulate the micro diversity system shown in Fig.2 , where three base stations (BSs) collaborate via a central backhaul processing (BPU) in the shaded three sector cluster. This simulation environment was also used in [14] and is sometimes referred to as an edge-excited cell. We consider the three BS scenario having either a single antenna or two antennas each to give nR = 3 or nR = 6 respectively. In the shaded coverage area of this edge-excited cell, we drop three or four users uniformly in space giving N = 3. |
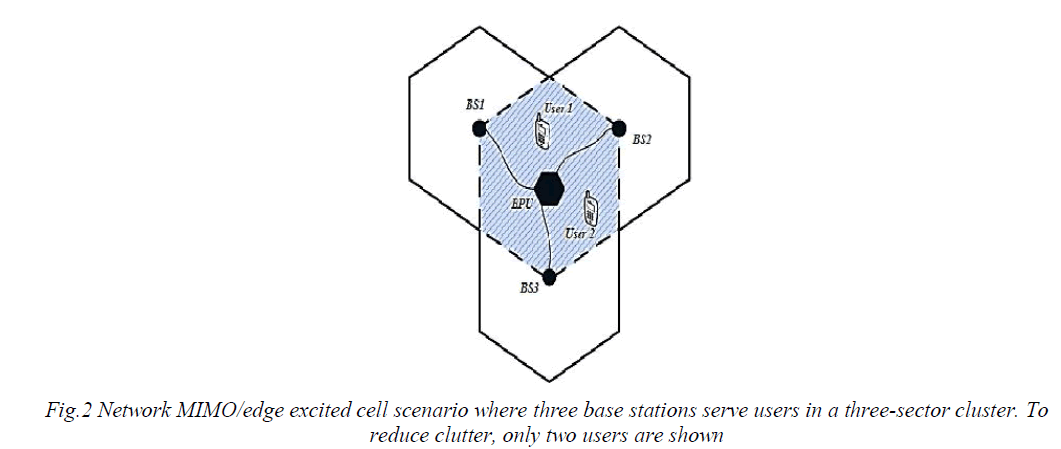 |
| N = 4. For each user, lognormal shadow fading and path loss is considered, where the standard deviation of the Fig. |
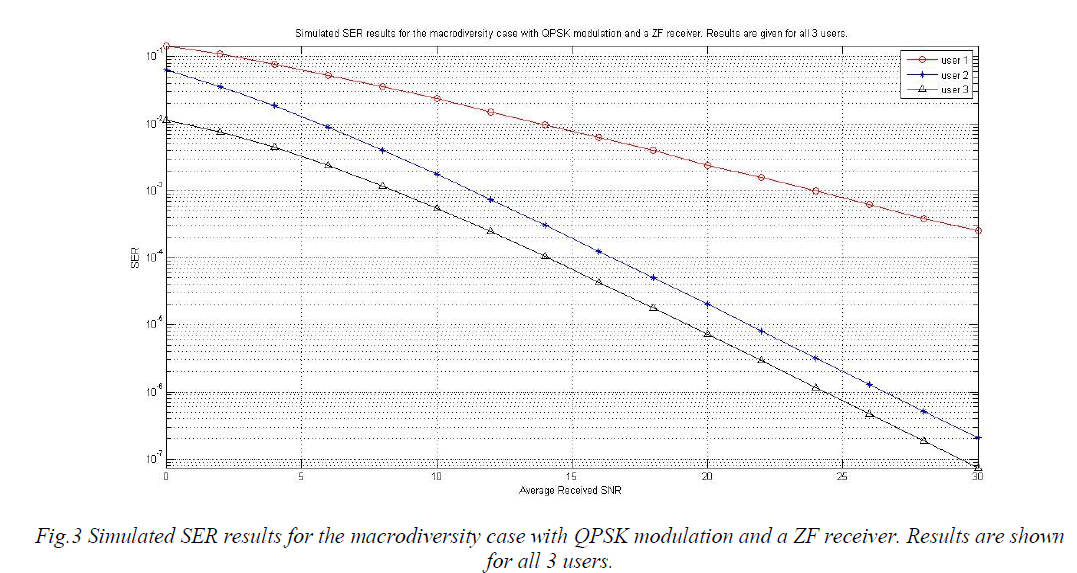 |
| shadowing is 8dB and the path loss exponent is Y=3.5. The transmit power of the sources is scaled so that the best signal received at the three BS locations is greater that 3dB at least 95% of the time. Even though the analysis in this paper is valid for any set of channel powers, the above methodology allows us to investigate the accuracy of the performance matrices for realistic sets of channel powers. In Figs.4, 5, 6 and 7, the case of three single antenna user sand three distributed BSs with a single receiver antenna is considered. Here, we investigate both the approximate SINR distributions and the approximate SER results for an MMSE receiver. |
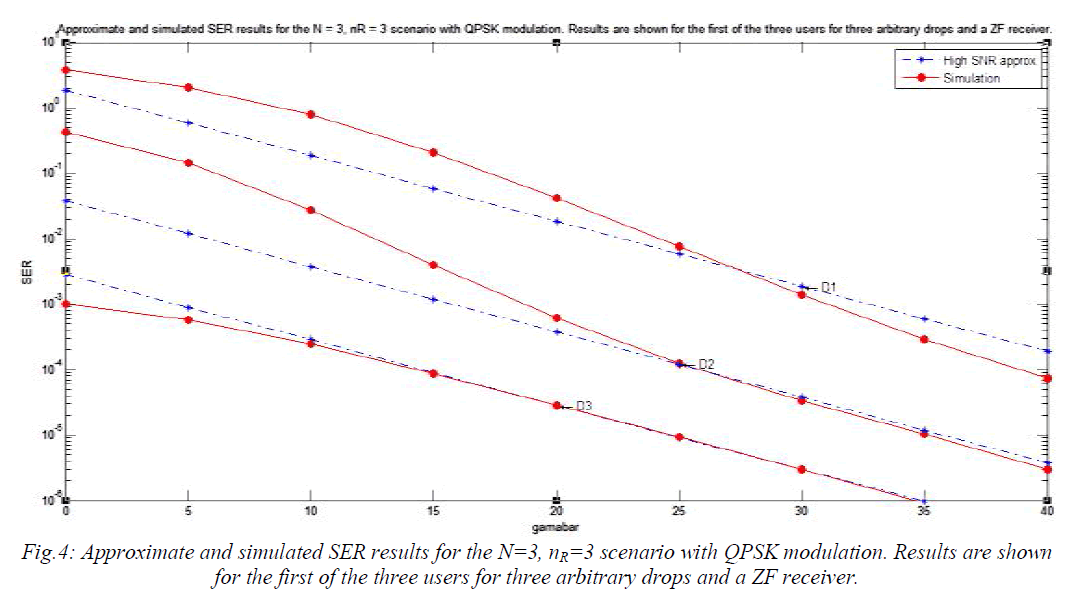 |
| In Fig.4, the approximate CDFs of the output SINR are plotted alongside the simulated CDFs. Results are shown for four random drops and, the results are for a particular user (the first of the three). The agreement between the CDFs is shown to be excellent. The agreement between the SER results is shown to be excellent across all three drops at SERs below 10-2. Again, this agreement is observed over a wide range with D1 having much higher SERs than D3. |
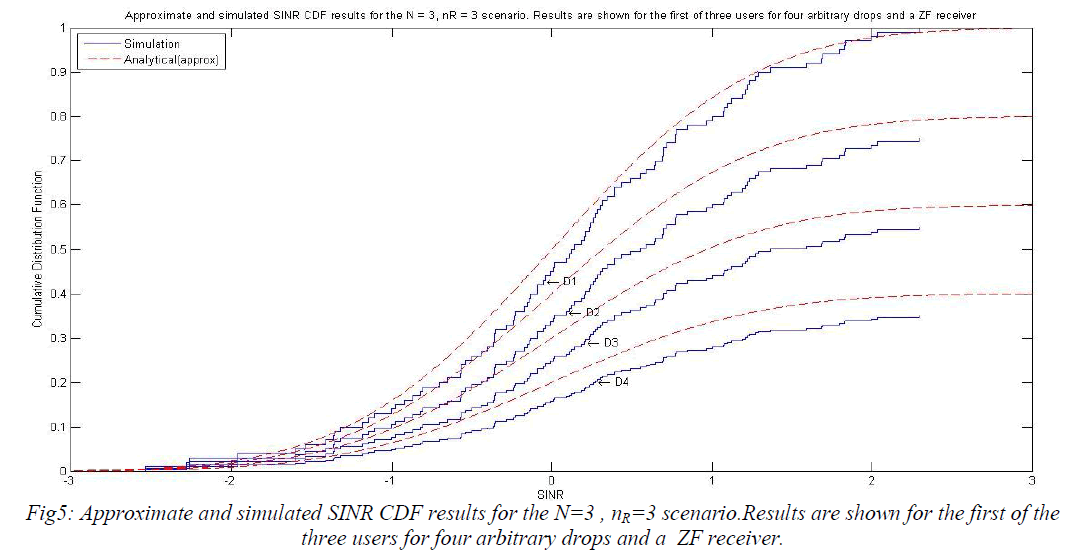 |
| In Fig.5, the approximate CDFs of the SNR are plotted alongside the simulated CDFs for a ZF receiver. Results are shown for four random drops. This is the companion plot to Fig.6 with the same system but a ZF receiver rather than an MMSE receiver. |
 |
| In Fig.6 and also in Figs.7-8 the SER is plotted against the transmit SNR, ïÿýïÿýÃÅÃâ¦. This is chosen instead of the receiver SNR to separate the curves so that the drops are visible and are not all superimposed, which tends to happen when SER is plotted against receive SNR. Note that this agreement is good across all drops, from D1 which has a very poor SINR performance to D4 with a much higher SINR performance. The use of physically motivated drops rather than ad-hoc scenarios is useful as it assesses the accuracy of the analysis in plausible channel conditions. |
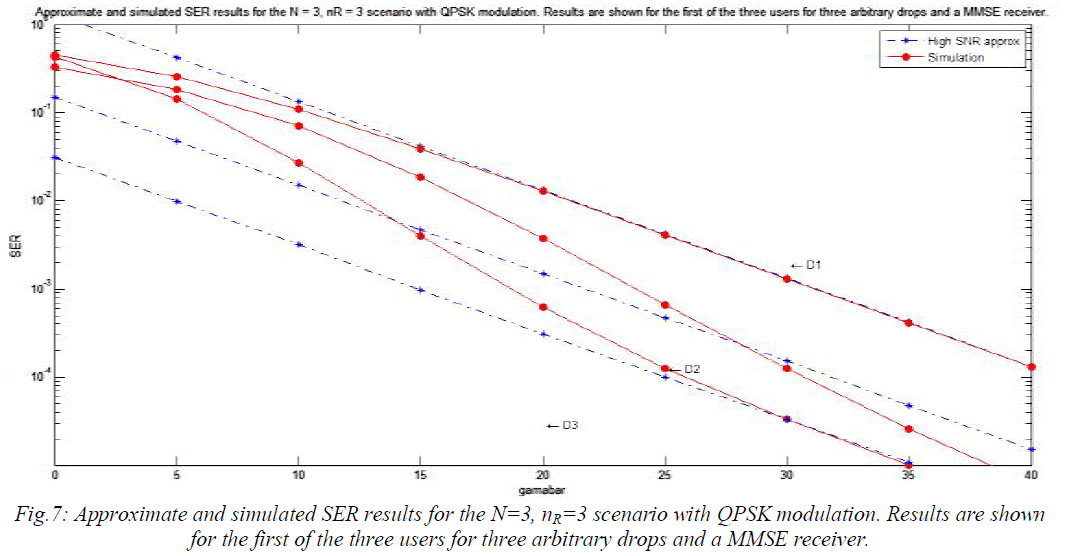 |
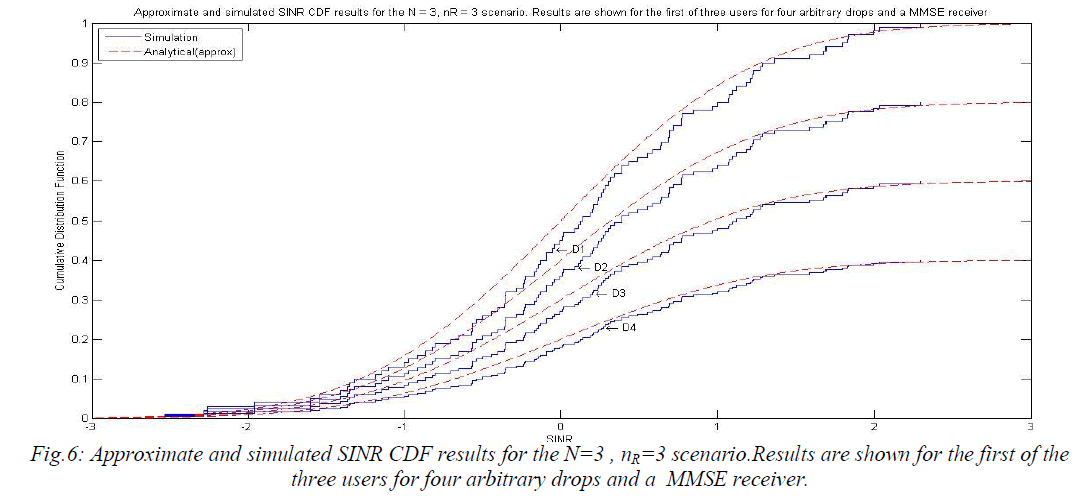
| This is the companion plot to Fig.4 with the same system but a MMSE receiver rather than an ZF receiver. Results are shown for both MMSE (Fig.7) and (Fig.8) with QPSK modulation. The agreement between the simulated SER and the high SNR approximation is shown to be less accurate in Fig 4, with very close agreement requiring low error rates around 10-4. |
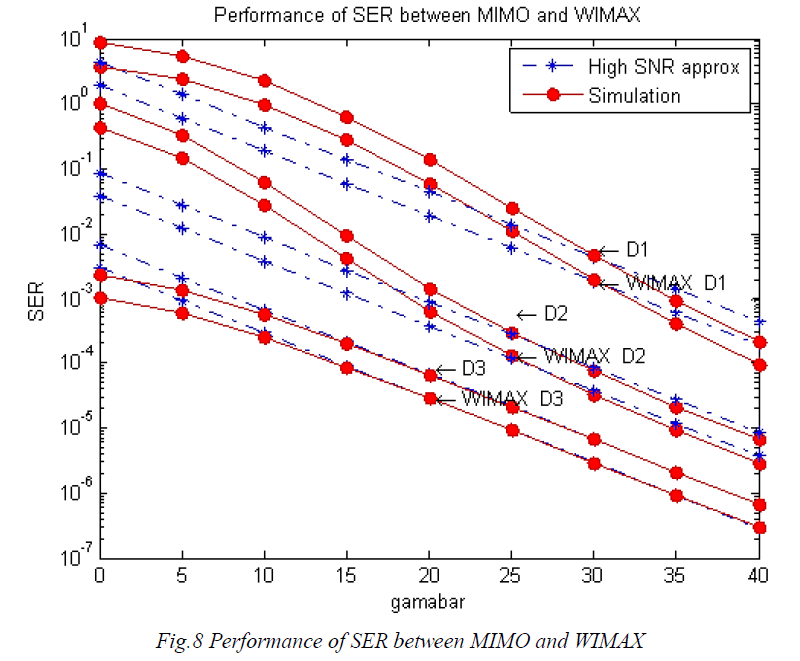 |
| Consider the simple SIR metric given by the sum of the first column of P (the total long term received power from the desired user I) divided by the sum of columns 2,3 and 4 (the total long term interfering power). In drops D1,D2 and D3 the SIR is -19dB, - 2.5dB and 6.5dB. As the SIR increases, the SER in Fig.8 drops. This is also shown by the K0 metric in which gives 17000, 323 and 13 for drops D1, D2 and D3. As SER increase with –K0 metric and the simple SIR metric give them same performance ranking with D3 the best and D1 the worst. The fourth drop, D4, is the interesting case. Here, the SIR is -10dB, which is lower than both D2 and D3. Hence, from Fig.8 D4 has a better SER performance than D2 and D3 despite having a worse SIR. In order to understand this, consider the P matrix for drop D4. |
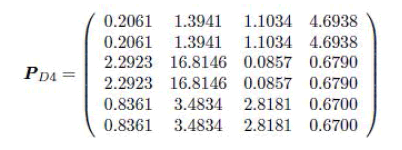 |
VII.WIMAX NETWORK (FUTURE WORK)
|
| World wide Interoperability for Microwave Access (WiMAX), is a wireless communications technology aiming to provide wireless data over long distances in a variety of ways as an alternative to cable and DSL, from point-to-point links to full mobile cellular type access. It is based on the IEEE 802.16 standard. The name WiMAX was created by the WiMAX Forum, which was formed in June 2001 as on industry-led, not-for-profit organization to promote conformance and interoperability of the standard. The goal of this deliverable is to provide an overview of the functionality and a description of the WiMAX network architecture. We study and assess the coexistence and interoperability solutions between WiMAX and other wireless access not work, such as WLAN (IEEE 802.16) in Beyond 3G (B3G) net works. We also evaluate the special features of the WiMAX technology, such as the improved coverage in Non Line Of Sight (NLOS) environments, in order to examine the applicability of well-known localization techniques. Finally, we can investigate the possibility of developing new localization technique that exploits the characteristics of WiMAX technology and the underlying network infrastructure to deliver improved positioning accuracy. |
VIII. CONCLUSION
|
| The performance of MMSE and ZF receivers is well-known in macro diversity systems where the receive antennas are collocated. However, in the macro diversity case, closed form performance analysis is a longstanding, unsolved research problem. In this paper, we make the progress towards solving this problem for the general case of an arbitrary number of transmit and receive antennas. The analysis is based on a derivation which targets that characteristic function of the output SINR. This leads to an expected value which is highly complex in its exact form, but can be simplified by the use of an extended Laplace type approximation. The SINR distribution is shown to have a remarkably simple form as a generalized mixture of exponentials. Also, the asymptotic SER results produce a remarkably compact metric which captures a large part of the functional relationship between the macro diversity power profile and SER. |
References
|
- S. Verdu, Multiuser Detection, 1st edition. Cambridge University Press,1998.
- J. H. Winters, “Optimum combining in digital mobile radio with cochannel interference,” IEEE J. Sel. Areas Commun., vol. SAC-2, pp. 528–539,July 1984.
- H. Gao, P. J. Smith, and M. V. Clark, “Theoretical reliability of MMSE linear diversity combining in Rayleigh-fading additive interferenceChannels,” IEEE Trans. Commun., vol. 46, no. 5, pp. 666–672, May 1998.
- J. H. Winters, J. Salz, and R. D. Gitlin, “The impact of antenna diversity on the capacity of wireless communication systems,” IEEE Trans.Commun., vol. 42, no. 2/3/4, pp. 1740–1751, Feb./Mar./Apr. 1994.
- Shah, A. M. Haimovich, M. K. Simon, and M.-S. Alouini, “Exact biterror probability for optimum combining with a Rayleigh fading Gaussiancochannel interferer,” IEEE Trans. Commun., vol. 48, pp. 908–912, Jun. 2000.
- M. Chiani, M. Z. Win, A. Zanella, R. K. Mallik, and J. H. Winters, “Bounds and approximations for optimum combining of signals in thepresence of multiple cochannel interferers and thermal noise,” IEEE Trans. Commun., vol. 51, pp. 296–307, Feb. 2003.
- D. A. Gore, R. W. Heath, Jr., and A. J. Paulraj, “Transmit selection in spatial multiplexing systems,” IEEE Trans. Commun., vol. 6, no. 11, pp.491–493, Nov. 2002.
- M. K. Karakayali, G. J. Foschini, and R. A. Valenzuela, “Network coordination for spectrally efficient communications in cellular systems,”IEEE Wireless Commun. Mag., vol. 13, no. 4, pp. 56–61, Aug. 2006.
- S. Venkatesan, A. Lozano, and R. Valenzuela, “Network MIMO: overcoming intercell interference in indoor wireless systems,” in Proc. 2007IEEE ACSSC, pp. 83–87.
- Sanderovich, O. Somekh, H. V. Poor, and S. Shamai “Uplink macrodiversity of limited backhaul cellular network,” IEEE Trans. Inf. Theory,vol 55, no. 8, pp. 3457–3478, Aug. 2009.
- E. Biglieri, R. Calderbank, A. Constantinides, A. Goldsmith, A. Paulraj, and H. V. Poor, MIMO Wireless Communication, 1st edition.Cambridge University Press, 2007.
- M. Sawahashi, Y. Kishiyama, A. Morimoto, D. Nishikawa, and M. Tanno, “Coordinated multipoint transmission/reception techniques for LTEAdvanced,”IEEE Wireless Commun. Mag., vol. 17, no. 3, pp. 26–34, Aug. 2010.
- L. Xiao, L. Dai, H. Zhuang, S. Zhou, and Y. Yao, “Information-theoretic capacity analysis in MIMO distributed antenna systems,” in Proc. 2003IEEE VTC, pp. 779–782.
- D. A. Basnayaka, P. J. Smith, and P. A. Martin, “Exact dual-user macrodiversity performance with linear receivers in flat Rayleigh fading,”in Proc. 2012 IEEE ICC, pp. 5626–5631.
- D. A. Basnayaka, P. J. Smith, and P. A. Martin, “Symbol error rate performance for macrodiversity maximal ratio combining in flat Rayleighfading,” in Proc. 2012 IEEE AusCTW, pp. 25–30.
- D. A. Basnayaka, P. J. Smith, and P. A. Martin, “Ergodic sum capacity of macrodiversity MIMO systems in flat Rayleigh fading,” submitted toIEEE Trans. Inf. Theory.
- S. Gradshteyn and I. M. Ryzhik, Table of Integrals, Series, and Products, 7th edition. Academic Press, 2000.
|