Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

PIXEL-LEVEL IMAGE FUSION USING BROVEY TRANSFORME AND WAVELET TRANSFORM

Rohan Ashok Mandhare1, Pragati Upadhyay2,Sudha Gupta3
  1. ME Student, K.J.SOMIYA College of Engineering, Vidyavihar, Mumbai, Maharashtra, India
  2. Assistant Professor, PVPP,COE. Sion, Mumbai, Maharashtra, India
  3. Associate Professor, K.J.SOMIYA College of Engineering, Vidyavihar, Mumbai, Maharashtra, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Remote sensing images fusion can not only improve the spatial resolution for the original multispectral image, but should also preserve the spectral information to a certain degree. Color transformation based image fusion methods have been implemented in various papers and this methods shows good spectral retention. This paper aims to implement pixel-level image fusion based on mathematical and wavelet transform image fusion methods and find out their capacity to improve spatial and spectral information. For this purpose different methods such as Averaging method, Multiplicative method, Brovey method, DWT method are implemented. Performance of this methods is evaluated with the help of assessment parameters such entropy, standard deviation, RMSE And PSNR. Experimental results shows that images merge by multiplicative and wavelet based method showed higher spatial resolution and better spectral features than the original image

Keywords
Image fusion, Brovey method, DWT, Entropy, RMSE, PSNR.

INTRODUCTION
Remote sensing offers a wide variety of image data with different characteristics in terms of temporal, spatial, radiometric and Spectral resolutions. For optical sensor systems, imaging systems somehow offer a trade off between high spatial and high spectral resolution, and no single system offers both. Hence, in the remote sensing community, an image with „greater quality‟ often means higher spatial or higher spectral resolution, which can only be obtained by more advanced sensors . The designing of a sensor to provide both high spatial and spectral resolutions is limited by the trade off between spectral resolution, spatial resolution, and signal-to-noise ratio of sensor. It is, therefore, necessary and very useful to be able to merge images with higher spectral information and higher spatial information [1].
Image fusion techniques can be classified into three categories depending on the stage at which fusion takes place; it is often divided into three levels, namely: pixel level, feature level and decision level of representation [2,3]. Many methods have been proposed for image fusion based on HIS transform, PCA transform and neural network approach. Among such methods, Multiplicative Transform, BROVEY transform and Wavelet based transform can quickly merge huge number of satellite images of high spatial resolution. Thus, in this paper, multiplicative transform, Brovey transform and wavelet transform methods are developed to merge LANDSAT MS image with LANDSAT PAN image.

MULTIPLICATIVE METHOD
The Multiplication model combines two data sets by multiplying each pixel in each band of the MS data by the corresponding pixel of the Pan data. [2].
The multiplicative method is derived from the four component technique. Crippen argued that of the four possible arithmetic methods only the multiplication is unlikely to distort the colors by transforming an intensity image into a panchromatic image Therefore this algorithm is a simple multiplication of each multispectral band with the panchromatic image
Red = (Low Resolution Band1 * High Resolution Band1)
Green = (Low Resolution Band2 * High Resolution Band2 )
Blue = (Low Resolution Band3 * High Resolution Band3)
The advantage of the algorithm is that it is straightforward and simple. By multiplying the same information into all bands. However, it creates spectral bands of a higher correlation which means that it does alter the spectral characteristics of the original image data.

BROVEY METHOD
The BT, established and promoted by an American scientist, Brovey, is also called the color normalization transform because it involves a red-green-blue (RGB) color transform method. The Brovey transformation was developed to avoid the disadvantages of the multiplicative method. It is a simple method for combining data from different sensors. It is a combination of arithmetic operations and normalizes the spectral bands before they are multiplied with the panchromatic image. It retains the corresponding spectral feature of each pixel, and transforms all the luminance information into a panchromatic image of high resolution[3].
The formulae used for the Brovey transform can be described as follows
Red = (band1/Σ band n)∗ High Resolution Band
Green = (band2/Σ band n)∗ High Resolution Band
Blue = (band3/Σ band n)∗ High Resolution Band
High resolution band = PAN [4].

DISCRETE WAVELET TRANSFORM: FIRST APPROACH
Wavelet transform is a mathematical tool developed in the field of signal processing. The wavelet transform decomposes the signal based on elementary functions: the wavelets. By using this, a digital image is decomposed into a set of multi resolution images with wavelet coefficients. For each level, the coefficients contain spatial differences between two successive resolution levels.
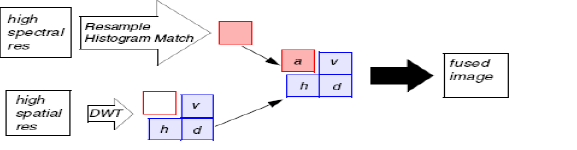image
As shown in block diagram PAN image is decomposed using DWT. The image wil get divided into four component namely approximation, digonal, vertical and horizontal. Out of this four component approximation component carries maximum information. Now this approximation component is replaced by MS image[5].
Processing steps of wavelet based image fusion
1- Decompose a high resolution P image into a set of low resolution P images with wavelet coefficients for each level.
2- Replace a low resolution P images with a MS band at the same spatial resolution level.
3- Perform a reverse wavelet transform to convert the decomposed and replaced P set back to the original P resolution level.
For the processing the replacement and reverse transform does three times, each for one spectral band.

DISCRETE WAVELET TRANSFORM: SECOND APPROACH
This is the second approach for wavelet based image fusion. In this method second level DWT of PAN & of MS image is taken. Then LL component in second level decomposition of MS image is replaced by the PAN image. By doing this minute details are obtained and hence there are more chances of obtaining better quality image[6].
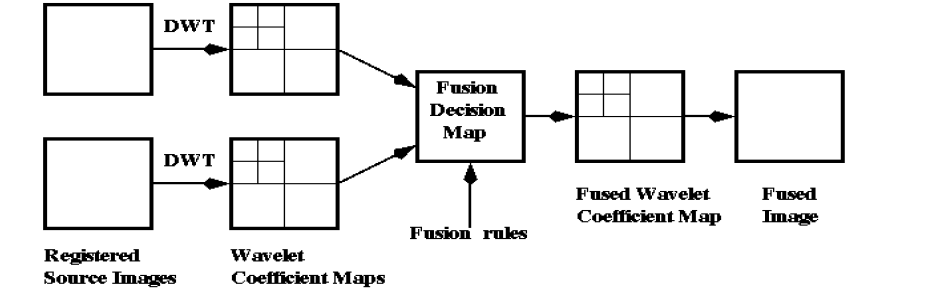image
Processing steps of wavelet based image fusion :
1- Decompose a high resolution P image into a set of low resolution P images with wavelet coefficients for each level.
2- - Decompose a low resolution MS image into a set of low resolution MS images with wavelet coefficients for each level
3- Replace a low resolution MS images with LL component of a PAN image a MS band .
4- Perform a reverse wavelet transform to convert the decomposed and replaced P set back to the original P resolution level.

EVALUATION PARAMETERS AND METHODS
In order to verify preservation of spectral characteristics and the improvement of spatial resolution, fused images are visually compared. The visual appearance may be subjective and depends on human interpreter. Along with visual analysis a number of statistical evaluation methods are applied to fuse image. This statistical methods gives idea about color preservation and spatial improvement. We make use of following methods:

A. Entropy
Entropy is defined as amount of information contained in a signal. Shannon was the first person to introduce entropy to quantify the information. The entropy of the image can be evaluated as
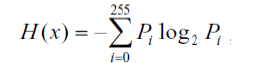image
Entropy can directly reflect the average information content of an image. The maximum value of entropy can be produced when each gray level of the whole range has the same frequency. If entropy of fused image is higher than parent image then it indicates that the fused image contains more information.

B.Standard deviation
This metric is more efficient in the absence of noise. It measures the contrast in the fused image. An image with high contrast would have a high standard deviation.
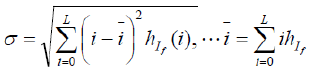image
Where hI f (i) is the normalized histogram of the fused image If (x,y) and L is number of frequency bins in histogram.

C.Root mean square error (RMSE)
A commonly used reference-based assessment metric is the root mean square error (RMSE) which is defined as follows:
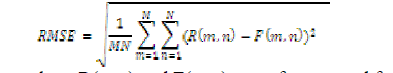image
where R(m,n) and F(m,n) are reference and fused images, respectively, and M and N are image dimensions.

D.Pick signal to noise ratio
PSNR computes the peak signal-to-noise ratio, in decibels, between two images. This ratio is used as a quality measurement between the original and a reconstructed image. The higher the PSNR, the better is the quality of the reconstructed image. To compute the PSNR, first we have to compute the mean squared error (MSE) using the following equation:
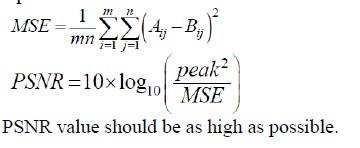image

RESULTS AND ANALYSIS
In our experiments two images are used to verify our result, first image is MS image taken by Landsat 7 ETM+ channel called as ITHAC as shown in fig1. This image is consist of 7 bands and 1000 no of columns and rows. Second image is false color image. Fig 3 shows PAN image of the same place taken by Landsat 7 ETM+ channel satellite.PAN image is consist of only 1 band.
In order to fully utilize spectral information of former and geometric information of latter, image fusion algorithm is applied. In addition to visual analysis, we conducted a quantitative analysis. In order to assess the quality of the fused images in terms of Entropy, Standard deviation, RMSE and PSNR.
image
image
Input images :-
Following data is used in this study.
image
Fig. 1 and Fig. 2 shows the input images used for experiment. Fig. 1 is MS image whereas the Fig.2 is PAN image. This images are taken by LANDSAT satellite. And this images are from same scene.
Output
Following are output images of various methods.
image
Fig 3 and fig 4 shows result Average method and Multiplicative method. We can see that images are well fused and will be easily giving more information from original image.
image
image
Fig.7 DWT2 method
Fig 5, Fig 6 and Fig 7 shows the result of Brovey, DWT1, DWT2 respectively. It is clear that in DWT2 we are getting color distortion.

CONCLUSION
In this paper five different methods like average method, multiplicative method, Brovey method and wavelet based methods are studied and compared with the help of assessment parameters. From table 1 it is clear that entropy of images merged by multiplicative methods or by wavelet based methods is higher than that of original image. This clearly indicates information content of fuse image is greater than that of original image. Also this table indicates averaging method contains more contrast. From visual point of view averaging method and Brovey method shows some color distortion. so in terms of both quality and quantity, information contain by mathematical and wavelet method is increase.

References