Keywords
|
| Antisway Tracking Control, fuzzy Logic Controllers, linguistic information, Defuzzification, Fuzzification Overhead crane systems have been widely used for material transportation in many |
INTRODUCTION
|
| industrial fields, due to their low cost, easy assembly and maintenance. But its severely nonlinear properties bring about undesired swings, especially at take-off and arrival. Thus its automization create severe problem as they belong to a class of under actuated mechanical systems, i.e., they have fewer actuators than degrees of freedom. Overhead crane systems belong to the category of incomplete control systems, which only allow a limited number of inputs to control more outputs. Such uncontrolled oscillations cause both stability and safety problems. This drawback strongly constrains the operational efficiency and the application domain.For example, 2-D overhead cranes have one control input (a trolley driving force) and two system variables to be controlled (a horizontal trolley position and a load swing angle). This underactuation property results in a coupling effect between the load sway motion and the trolley travelling motion. In addition, uncontrolled load sway dynamics causes safety problems in crane systems, which makes it much more challenging to control them. Crane control systems have beendeveloped in such a way that the trolley is moved to a desired position as fast as possible while adequately suppressing the load swing angle[1]-[3]. |
LITERATURE SURVEY
|
| Since fuzzy logic controller can mimic human behaviour, many researchers applied fuzzy logic controller to control either overhead crane, gantry crane as well as rotary crane. A thorough literature overview was done on the usage of fuzzy logic controller as applied to the various crane systems. Lee, H. H. and Cho, S. K. (2001) proposed a new fuzzy logic anti swing control for industrial three dimensional overhead cranes. However, PID controller still approached for position control which is based on model controller. Omar, H.M (2003) proposed a controller with robust and fast for gantry and rotary cranes. The result shows that the fuzzy logic controller has smaller transfer time and overshoots unfortunately, with higher swing angles. Besides, the fuzzy logic controller uses mapping method which needs delayed feedback controller before fuzzy logic can be designed thus resulting time consuming. Wahyudi&Jalani, J. (2005) designed and implemented robust Fuzzy Logic Controller for An Intelligent Gantry Crane System. The experimental results for antiswing control successfully proved that fuzzy logic controller is better compared to the conventional PID controller. However, the application of the fuzzy logic 6 controller that has been proposed is for gantry crane which is their parameter is totally different with rotary crane. Othman, M. Z. (2006) proposed a rough controller as a replacement for fuzzy logic controller which is based on mathematical computation to control the overhead travelling crane. The result shows that, it is just satisfactory, even more the quality index for both controllers does not differ very much. The complex mathematical modelling involves in designing process is not practicable.Ruslee, R.Jalani, J. & Abdullah, J. (2008) proposed Anti-Swing Control Strategy for Automatic 3 D.O.F. Crane System Using Fuzzy Logic Controller. The simpler and practical design of fuzzy logic controller applied for both position and anti swing control. It is obvious that the performance of fuzzy logic controller is better compared to Linear Quadratic Regulator (LQR) controller. Based on those related work, the researchers make a great efforts to propose the good controller in the industrial setup to overcome the crane problems. Their applications of each method differ and still, the fuzzy logic controller is better controller compared to other conventional controller yet. Thus, the further investigation of this controller is needed in depth. The approach of this study is similar to Ruslee, R. Jalani, J. & Abdullah, J. (2008) in designing the fuzzy logic controller but for position control only. The investigation will be based on the different types of membership function applied on fuzzy logic controller. |
MATHEMATICAL MODELLING
|
| A two-dimensional overhead crane system, which has the capabilities of both traversing and hoisting, is considered in this research. Most crane systems used for loading and unloading at a dock or for assembly in a factory have similar structures (Fig 1). This kind of crane system has two actuators, responsible for horizontal and vertical motions, respectively. Nevertheless, three controlled variables, horizontal and vertical displacements as well as the swing angle, need to be equally considered. |
| This system is an incomplete control system because it has a smaller number of actuators than the number of controlled variables |
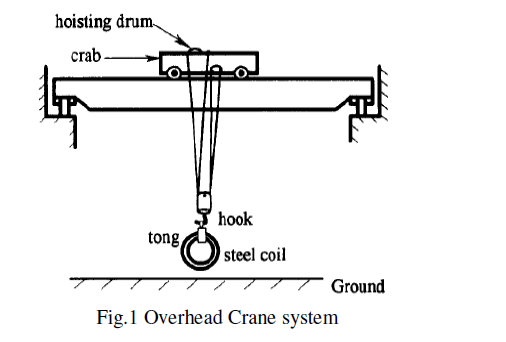 |
| In order to simplify the modelling complexity, several assumptions have first to be made: |
| ïÃâ÷ Plastic deformation inthe system is ignored. |
| ïÃâ÷ The cable is treated as a weightless rigid body. |
| ïÃâ÷ The moment of inertia of the load is ignored and the load becomes a point mass. |
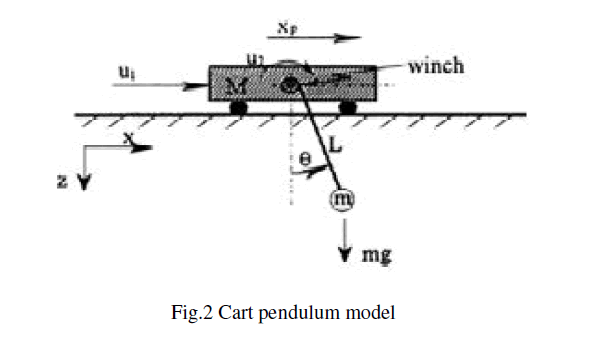 |
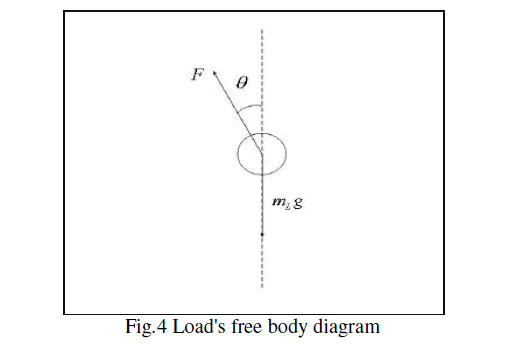
| Therefore, the overhead crane system can be simplified to a cart-pendulum model with a variable pendulum length, as shown in Fig 2. U1 is the force exerted by the horizontal actuator and U2 is the applied torque from a rotational actuator acting on a winch with a radius R. The masses of the cart and the load are denoted by M and m. xp is the horizontal displacement and Ãâó indicates the inclination swing angle. L represents the cable length and J stands for the moment of inertia of the winch. Mathematical model for this system was derived using newton’s second law[10]. The dynamics of the system was analysed by splitting the system into two parts, which are cart and load |
| For both cart and load, the free body diagram considered for mathematical derivation is shown in Fig 3 and Fig 4 respectively. |
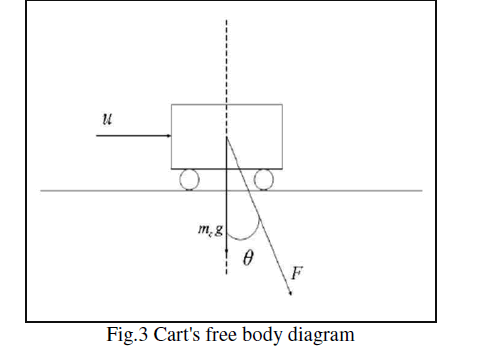 |
 |
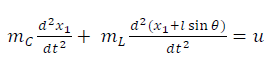 |
 |
 |
MATLAB SIMULATION AND MODEL VERIFICATIOON
|
| Matlab Simulink is used by putting the respective block functions according to our requirement and configures the values. For this study, the open-loop Simulink setup is shown in fig 5. |
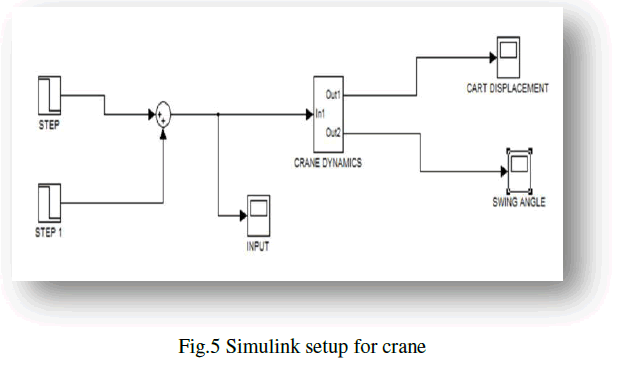 |
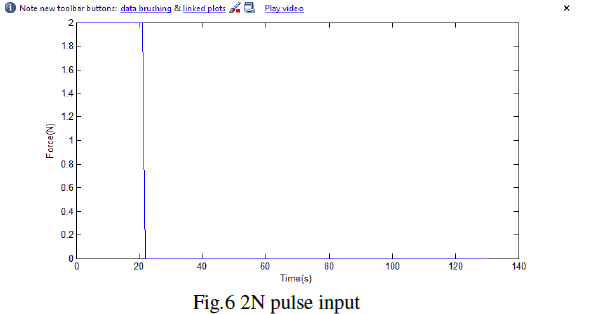
| As can be seen in fig 5, step input block is used as input source for the crane dynamics. For initial testing, parameter variable were fixed at constant value. For first simulation testing, input was given as 2N for 10 second as shown in fig 6. |
 |
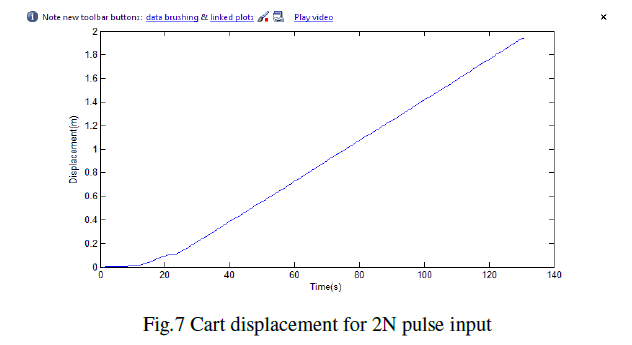
| The resultant displacement and oscillation is seen in fig 7 and fig 8 respectively. |
 |
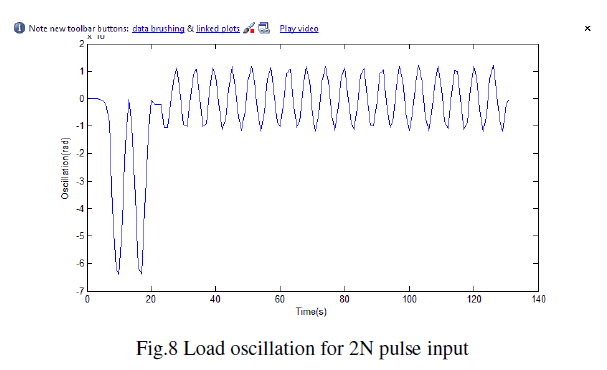 |
| From fig 7 and fig 8, the cart displacement moved to “infinity”, while the load swing is within -1 to 1 radians. From the observation, it is clear that the cart does not stop at all, and thus it is necessary for the input to be modified so that the cart will stop after a certain distance |
| When the value ofpayload is changed, the response of system in terms of cartposition and load sway angle is also expected to change. Same goes for PID controller.An optimized PID controller for a fixed set of parameters would not yield an optimizedresponse when the parameters are changed. This is because it is a nature of PID controllerto not be able to satisfy the expected system performance when disturbance or parametervariance occurs. This can be rectified by implementing fuzzy-tuned PID controller. |
| Once the dynamic equation of gantrycrane managed to be verified, next step is to design a PID controller, followed by fuzzytuner for PID gains. |
PID DESIGN FOR POSITION CONTROL
|
| PID controller used for this project will be optimized using Ziegler-Nichols method.The Ziegler-Nichols tuning method is a heuristic method of tuning a PID controller. It was developed by John G. Ziegler and Nathaniel B. Nichols. It is performed by setting the I (integral) and D(derivative) gains to zero. The P(proportional) gain, KP is then increased (from zero) until it reaches the ultimate gain Ku, at which the outputof the control loop oscillates with a constant amplitude KU the oscillation period TU are used to set the P,I and D gains depending on the type of controller used. |
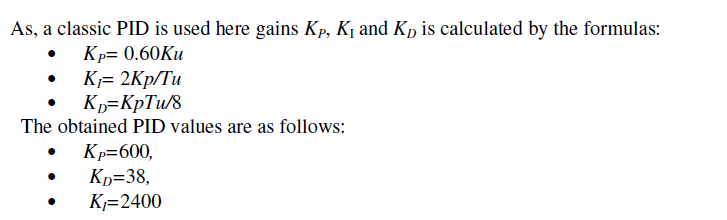 |
 |
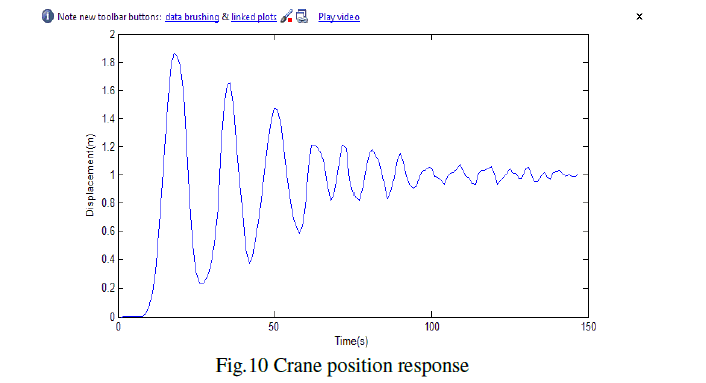 |
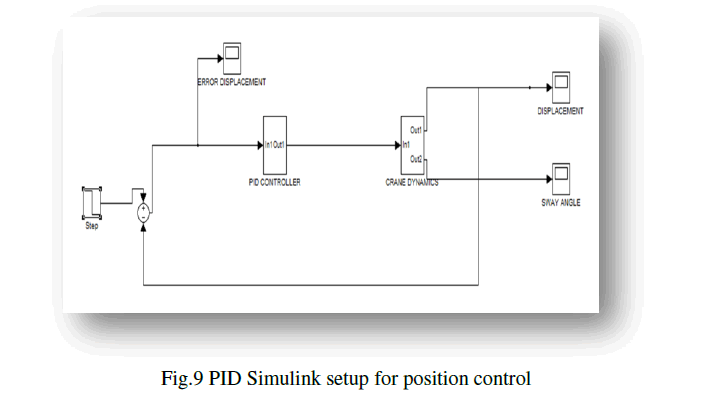
| The PID Simulink setup shown in fig. 9 makes the crane to move in a position as shown in fig. 10. As the figureitself suggest that the response of the crane has improved a lot. The oscillation in the response is decreasing with increasing time. Which increase the performance of the system heavily. |
| From fig 8 and fig 9 we can see that percentage of overshoot for crane position is 2.3% while settling time is 4.136s. |
FUZZY LOGIC AS PID GAINS TUNER FOR POSITION CONTROL
|
| For the purpose of this project, Mamdani fuzzy inference system has been designed as fuzzy-tuner. This system receives error and error rate as its input and has three different outputs, which are PID gains tuner. The fuzzy system for the input has three triangular members. On other hand, output for KP has three triangular members, while output for KD and KI consists of two triangular functions. The width of each membership was chosen according to determined range or universe of discourse. These values were constantly modified throughout the project to obtain the best result. |
 |
| FPID results in overall better response in terms of percentage of overshoot and also settling time. It is also observable that the highest percentage of overshoot for FPID is 1.8% which makes it more suitable than PID controller for usage in environment with constant parameter change. FPID also yields a much better performance of sway angle. |
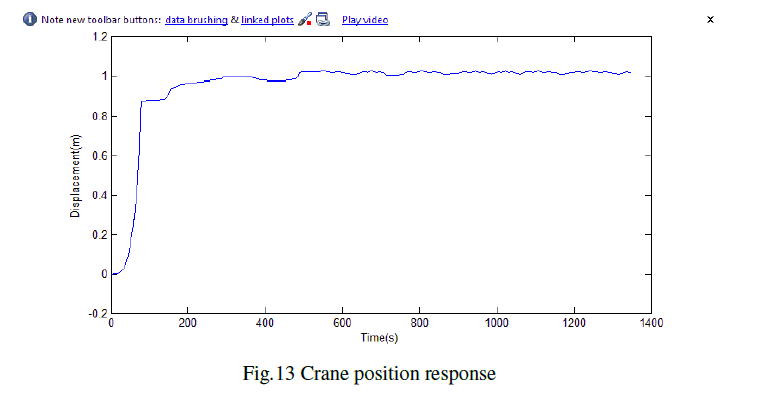 |
COMPARISION BETWEEN PID AND FUZZY-TUNED PID CONTROL SCHEME
|
| When the value ofpayload is changed, the response of system in terms of cart position and load sway angle is also expected to change. Same goes for PID controller, an optimized PID controller for a fixed set of parameters would not yield an optimized response when the parameters are changed, this is because it is a nature of PID controller to not be able to satisfy the expected system performance when disturbance or parameter variance occurs, this can be rectified by implementing fuzzy-tuned PID controller. When a comparative study for conventional PID controller with fuzzy-tuned PID one had been affected, then the comparative results are found at different set point values. |
| When considering of rising time in seconds, maximum overshoot,maximum overshooting in case of disturbance submission and steady-state error it could conclude that the overall steady state and dynamic performance of the proposed fuzzy-tuned PID controller plant seems to be better than that it was with classical approach (PID). It could be noticed the fuzzy-tuned PID based control approach has enhanced the robustness and reduced the settling time. The sensitivity of the closed-loop response against an effectiveness parameter variation and disturbances has been also modified. |
| The used method with the unified universe of discourse, stated in this article, considerably simplifies setting of fuzzytuned PID controllers. It allows approximate adjustment of controller’s parameters according to well known methods for PID controller synthesis. If the universe has non-linear membership function layout then the results can have better behaviour than the classic PID controller. The fuzzy-tuned PID controller can be programmed like a unified block in a controller and therefore work consumed on an implementing to the particular control system. |
SIMULATION AND RESULTS
|
| Single input fuzzy logic control(SIFLC) is a simplification of conventional fuzzy logic controller(CFLC). It is achieved by applying the signed distance method where the input to SIFLC is only one variable known as “distance”. This is in contrast to the CFLC which requires an error and the derivative (change) of the error as its inputs. The reduction in the number of inputs simplifies the rule table to one-dimensional, allowing it to be treated as a single input single output(SISO) controller. Typically, a FLC has two controlled inputs, namely error (e) and the change of error (Δe). Instead of using two –variable input sets (e, Δe), it is possible to obtain the corresponding output, uousing a single variable input only, this is called signed distance method. This method simplifies the number of inputs into a single input variable known as distance,d .The distance represents the absolute distance magnitude of the parallel lines (in which the input set of e and Δe lies ) from the main diagonal line. |
| The above model concerning the fuzzy PD-based overhead crane system has been designed and validated with MATLAB/SIMULINK. The first part of the research was done using a linearized model of gantry crane, while once the full construction of control design is complete, non-linearized model was used. Linearized model was implemented by using built-in “state-space” block because the model was in typical state space form. Non-linearized on other hand was implemented using built-in “function” block because of non-linear form of equation such as trigonometry functions. The obtained comparative results for both fuzzy PD and classical PD as positioning control and anti-swing compensation have been extracted with considering the setpoint tracking problems and the step disturbance rejection.So it is concluded that the performance of the closed loop control system using Fuzzy PD, when tracking the reference position Xref, is being enhanced with modification in dynamic state comparing with classical PD control structure. While the effect of the swing angle has been well eliminated using the proposed Fuzzy PD-controlled structure comparing with classical PD one.FPID results in overall better response in terms of percentage of overshoot and also settling time. It is also observable that the highest percentage of overshoot for FPID is 1.8% which makes it more suitable than PID controller for usage in environment with constant parameter change. FPID yields a much better performance of sway angle. |
| If PID and FPID compared, FPID has a better ability of robustness which enables it to cope with parameter change. FPID can be further improved by adding another feedback for anti-sway control. This improved controller, in form of FPID + FPD might not be the best position controller or anti-sway controller, but it does have a good balance between both of them and results in overall better performance. Higher levels of hook and sway angle reduction were obtained using SIFLC with three modes shaper as compared to the case with single and two modes shaper. In addition, three modes shaper also produce no overshoot in cart position response as compared to the other cases. But with higher mode shaper, the cart position response is slower as compared to lower number of mode combinations. |
CONCLUSION
|
| Most overhead crane systems belong to the group of incomplete control systems. Undesired oscillatory behaviour may occur during the control process, due to smaller number of control efforts than the number of specifications. A fuzzy controller was applied to an overhead crane system, to reduceswing phenomena during the transport process and overcome possible loading uncertainty. Since the control mechanism is based on trial and error method and human expertise, so there are chances of error. |
References
|
- H. H. Lee, “Modeling and control of a three-dimensional overhead crane,”Trans. ASME, J. Dyn. Syst. Meas. Control, vol. 120, no. 4, pp.471–476, Dec. 1998.
- Y. Fang, W. Dixon, D. Dawson, and E. Zergeroglu, “Nonlinear coupling control laws for an underactuated overhead crane system,”IEEE/ASMETrans. Mechatronics, vol. 8, no. 3, pp. 418–423, Sep. 2003.
- H. Park, D. Chwa, and K. S. Hong, “A feedback linearization control of container cranes: Varying rope length,” Int. J. Control Autom.Syst., vol. 5, no. 4, pp. 379–387, Aug. 2007.
- H. H. Lee, “An anti-swing trajectory control of overhead cranes with high speed hoisting,” in Proc. Amer. Control Conf., Denver, CO,Jun. 2003, pp. 1440–1445.
- H. Lee, Y. Liang, and D. Segura, “A new approach for the antiswing control of overhead cranes with high-speed load hoisting,” Int. J.Control, vol. 76, no. 15, pp. 1493–1499, Oct. 2003
- H. Lee, Y. Liang, and D. Segura, “A sliding-mode antiswing trajectory control for overhead cranes with high-speed load hoisting,” Trans.ASME,J. Dyn. Syst. Meas. Control, vol. 128, no. 4, pp. 842–845, Dec. 2006.
- H. Lee, “Motion planning for three-dimensional overhead cranes with high-speed load hoisting,” Int. J. Control, vol. 78, no. 12, pp. 875–886, Aug. 2005.
- J. H. Yang and K. S. Yang, “Adaptive coupling control for overhead crane systems,” Mechatronics, vol. 17, no. 2/3, pp. 143–152,Mar./Apr. 2007.
- J. H. Yang and K. S. Yang, “Adaptive control for 3-D overhead crane systems,” in Proc. Amer. Control Conf., Minneapolis, MN, Jun.2006,pp. 1832–1837.
- Zairulazha.Z.Modeling and Vibration control of a Gantry Crane, Master’s Thesis(2005) pp. 21-35.
- Hans Butler, GerHonderd and Job Van Amerongen. Model Reference Adaptive Control of a Gantry Crane Scale Model. IEEE ControlSystems 1991,1991. pp. 57 -62.
- Kurrer, Karl-Eugen. The history of the theory of structures: from arch analysis to computational mechanics. Berlin: Ernst &Sohn (2008).pp. 411–415
- Dey.R, Sinha.N, Chaubey.P and S. Ghosh and G. Ray. Active Sway Control of a Single Pendulum Gantry Crane System using Output-Delayed Feedback Control Technique. Int. Conf. Control, Automation, Robotics and Vision Singapore (2010),pp. 532-536.
- Solihin.MA, Wahyudi, and Albagul.A. Development of Soft Sensor for Sensorless Automatic Gantry Crane Using RBF Neural Networks,IEEE Journal (2006)Solihin.M.A and Wahyudi. Fuzzy-tuned PID Control Design for AutomaticGantry Crane, International Conferenceon Intelligent and Advanced Systems (2007). pp.1092-1097.
- Zairulazha.Z. Modeling and Vibration Control of a Gantry Crane, Master’s Thesis (2005) Pg. 21-35.
- C.R. Houck, J.Joines, and M.Kay. A genetic algorithm for function optimization: A Matlabimplementation. ACM Transactions onMathematical Software, (1996)C.L. Teo, C.J. Ong and M. Xu. Pulse Input Sequences for Residual VibrationReduction. Journal of Soundand Vibration 1998, 1997. 211(2): 157 - 177.
- Jan Jantzen. Foundations of Fuzzy Control. John Wiley & Sons Ltd. (2007). pp.71-115
- Z.Huaguang, L.Derong. Fuzzy Modeling and Fuzzy Control. BirkhauserBoston(2006).
- Wahyudi, Jalani, J., Muhida, R., and Salami, M. J. E., 2007, “Control strategy for automatic gantry crane systems: a practical andintelligent approach,” International Journal of Advanced Robotic Systems 4, 447–456.
- Trabia, M. B., Renno, J. M., and Moustafa, K. A. F., 2006, “A general anti-swing fuzzy controller for an overhead crane with hoisting,” inProceedings of the IEEE International Conference on Fuzzy Systems, Vancouver, Canada, July 16–21.
- Singhose, W. E., Porter, L. J., and Seering, W. P., 1997, “Input shaped control of a planar gantry crane with hoisting,” in Proceedings ofthe American Control Conference, Albuquerque, NM, June 4–6, pp. 97–100.
- Singhose, W. E., Porter, L. J., and Seering, W. P., 1997, “Input shaped control of a planar gantry crane with hoisting,” in Proceedings ofthe American Control Conference, Albuquerque, NM, June 4–6, pp. 97–100.
- Renno, J. M., Trabia, M. B., and Moustafa, K. A. F., 2004, “Anti-swing adaptive fuzzy controller for an overhead crane with hoisting,” inProceedings of IMECE ASME International Mechanical Engineering Congress & Exposition, Anheim, CA, November 14–19.
- Park, B. J., Hong, K. S., and Huh, C. D., 2000, “Time-efficient input shaping control of container crane systems, in Proceedings of IEEEInternational Conference on Control Application, Anchorage, AK, September, pp. 80–85.
- Omar, H. M., 2003, Control of Gantry and Tower Cranes, PhD Dissertation, Virginia Polytechnic Institute and State University,Blacksburg, Virginia.
|