POWER QUALITY CONTROL IN
DISTRIBUTED GENERATION SYSTEMS
USING SHUNT ACTIVE POWER FILTER

Hema.D; Bhavana.K

POWER QUALITY CONTROL IN DISTRIBUTED GENERATION SYSTEMS USING SHUNT ACTIVE POWER FILTER

Hema.D¹,Bhavana.K²

Student, Dept. of EEE, PVPSIT,Vijayawada, Andhra Pradesh, India
Asst.Professor, Dept. of EEE, PVPSIT,Vijayawada, Andhra Pradesh,India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Due to the wide spread of power electronics equipment in modern electrical systems, the increase of the harmonics disturbance in the ac mains currents has became a major concern due to the adverse effects on all equipment. Power electronic converters are commonly used for interfacing distributed generation (DG) systems to the electrical power network. In DG systems a fast and accurate positive-sequence, fundamental grid-voltage frequency and magnitude tracking is required to synchronize grid connected converter-systems with the mains. This paper deals with a single phase inverter for DG systems requiring power quality features, such as harmonics and reactive power compensation for grid-connected operation. The idea is to integrate the DG unit functions with shunt active power filter capabilities. With this approach the inverter controls the active power flow from the renewable energy source to the grid and also performs the nonlinear load current harmonic compensation. The effectiveness of the proposed method is investigated using a detailed mathematical analysis. In particular, active power control plays an important role both during grid faults and in normal conditions. The usefulness of the simulation approach to APF is demonstrated so APF designers have a better insight using Matlab Simulink in order to develop new APFs.

Keywords

Active Power Filters, Simulation, Current Harmonics, Reactive Power, Unbalance

I. INTRODUCTION

The distributed generation (DG) concept emerged as a way to integrate different power plants, increasing the DG owner’s reliability, reducing emissions, and providing additional power quality benefits [1]. Modern electrical systems, due to wide spread of power conversion units and power electronics equipments, causes an increasing harmonics disturbance in the ac mains currents. These harmonics currents causes adverse effects in power systems such as overheating, perturbation of sensitive control and communication equipment, capacitor blowing, motor vibration, excessive neutral currents, resonances with the grid and low power factor . As a result, effective harmonic reduction from the system has become important both to the utilities and to the users. The solution over passive filters for compensating the harmonic distortion and unbalance is the shunt active power filter (APF). The APF is actually an inverter that is connected at the common point of coupling to produce harmonic components which cancel the harmonic components from a group of nonlinear loads to ensure that the resulting total current drawn from the main incoming supply is sinusoidal[2]. Shunt APFs are the most commonly used topology and they are connected in parallel with the AC line. APFs have certain advantages if compared to the passive power filters. They are known to be able to adapt concurrently to changing loads, can be expanded easily and will not affect neighborhood equipments. Generally the APFs are smaller and their prices are comparable or less than a passive solution. [3].In order to compensate the distorted currents the APF injects currents equal but opposite with the harmonic components, thus only the fundamental components flows in the point of common coupling (PCC) as in equation (1):

This paper proposes and validates an enhanced power quality control strategy for single-phase inverters used in DG systems.

The idea is to integrate the DG unit functions with shunt APF capabilities. With the proposed approach, the inverter controls the active power flow from the energy source to the grid and also performs the compensation of reactive power.The APF, connected in parallel to the disturbing non-linear loads is as seen in figure 1, causes the supply currents to be near sinusoidal and balanced.

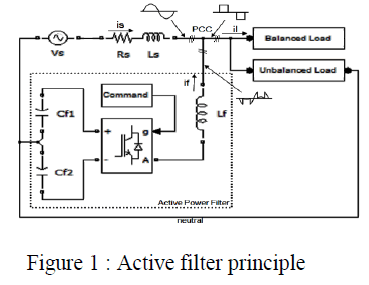II.NON-LINEAR LOAD

Nonlinear loads are loads in which the current waveform does not take the shape of the applied voltage waveform due to a number of reasons, for example, the use of electronic switches that conduct load current only during a fraction of the power frequency period. There are many nonlinear loads drawing nonsinusoidal currents from electrical power systems.

These non sinusoidal currents pass through different impedances in the power systems and produce voltage harmonics. These voltage harmonics propagate in power systems and affect all of the power system components. [2, 4,5].

III.HARMONICS SOURCES AND EFFECTS

Generally every device that use power electronic components such as renewable electrical power generation systems, cycloconverters, electronic phase control loads, and pulse width modulation (PWM) drives produce harmonics [2, 5]. Among the most common nonlinear loads in power systems are all types of rectifying devices like those found in power converters, power sources, uninterruptible power supply (UPS) units, and arc devices like electric furnaces and fluorescent lamps. Even linear loads like power transformers can act nonlinear under saturation conditions. These type of non linear loads are the most popular kind which are used in most electrical devices such as mobile cell charger, LCD, PC computer and monitors, and they are used in a very large range in life [5]. The effects of harmonics in power systems and electrical loads are described as the disturbance to Electric and Electronic Devices, and higher losses [5].

IV.ACTIVE AND REACTIVE POWER CONTROL

The integration of APF capability in single-phase inverters needs a particular attention since the control techniques were developed for three phase APFs, and consequently, must be adapted for single-phase systems. The literature presents different solutions to compute the harmonic extraction task for single-phase APFs [6]–[7]. The methods are classified in direct and indirect methods in [6]. The direct methods include the Fourier transform method [8], the instantaneous reactive power (IRP) theory [9]–[10] and the synchronous reference frame (SRF) theory [11]-[12]. On the other hand, the indirect methods include the use of enhanced phase-locked loop (EPLL) scheme or a controller such as proportional–integral (PI) to find the reference current [6], [7]. Among these solutions, the IRP and the SRF theories are the most addressed ones in the literature [9]–[12]. These strategies were originally proposed for three-phase systems, but they can be adapted for single-phase systems due to their effectiveness. In three-phase systems, both IRP and SRF techniques operate in a reference system with two orthogonal axes (αβ for IRP and dq for SRF). In singlephase systems, since only one-phase variable exists, it is necessary to create one “fictitious” or imaginary variable in which all frequencies are phase-shifted by 90 electrical degrees with respect to the original variable. With this procedure, a system with two orthogonal variables is created from a single variable, allowing the application of the IRP and SRF theories. However, the computation of the fictitious variable from the existing one is not a simple task since the nonlinear load current has a high harmonic content. The imaginary variables are calculated in [10] by using the Hilbert transform. This method leads to a noncausal system and cannot be directly implemented. Some phase delays are introduced in the fictitious variable and implicitly in the inverter current reference [13]. Alternatively, the computation

of the reference current can be performed by using a sinusoidal signal integrator (SSI) along with the IRP theory. This approach has been originally proposed by the authors in [14] and allows obtaining without any delay the fictitious variables that are needed to apply the IRP theory or other techniques originally applied for three-phase systems. Moreover, the reference current computation is insensitive to grid voltage distortions. The authors in [14] experimentally validated only the current harmonics compensation features of the strategy since the inverter has been operated only as an active filter. This paper shows the complete experimental validation of the proposed method for all its features, i.e., active and reactive power generation along with current harmonics compensation. Active and reactive power control theory was proposed by Akagi et al. in 1983 . According to the p-q theory, the active, reactive and zerosequence powers are defined as in equations (3 and 4) and (5):

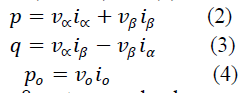The currents, voltages and powers in the α-β system can be decomposed in mean and alternating values, corresponding to the fundamental and harmonic components, as in equation (5).

where x can be currents, voltages or powers.

The power components have the following physical meaning (Afonso J.L. et al., 2003):

V.SIMULINK RESULTS

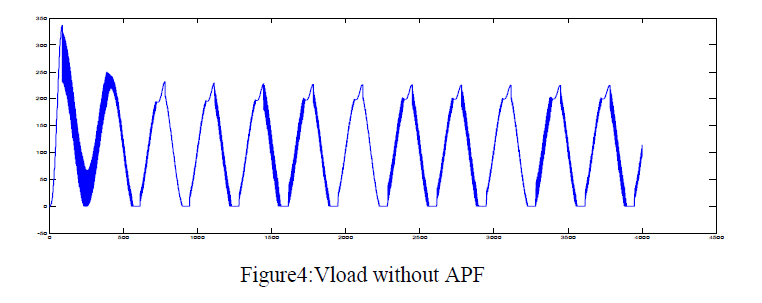
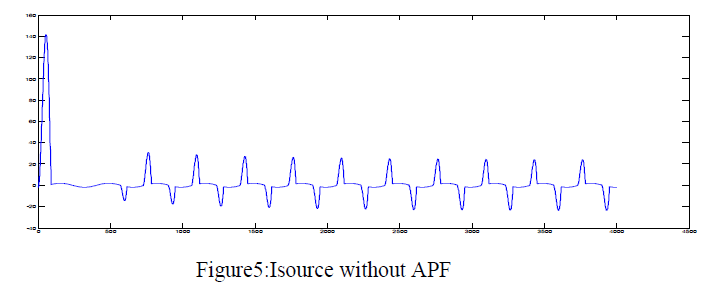
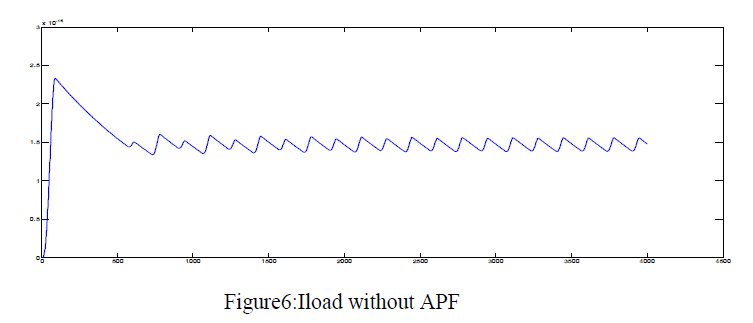
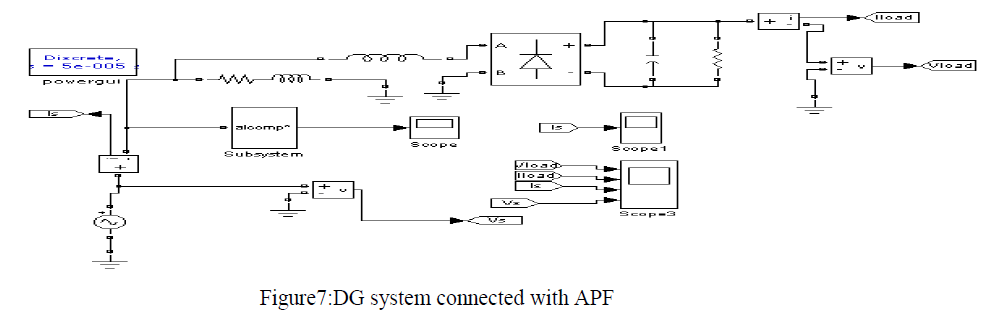
In this paper the DG system and its performance is compared without APF and with APF. The source voltage, source current, non-linear load voltage, non-linear load current without and with APF are compared.The overall system model containing the power source, without the APF and the nonlinear loads is shown in figure 3.

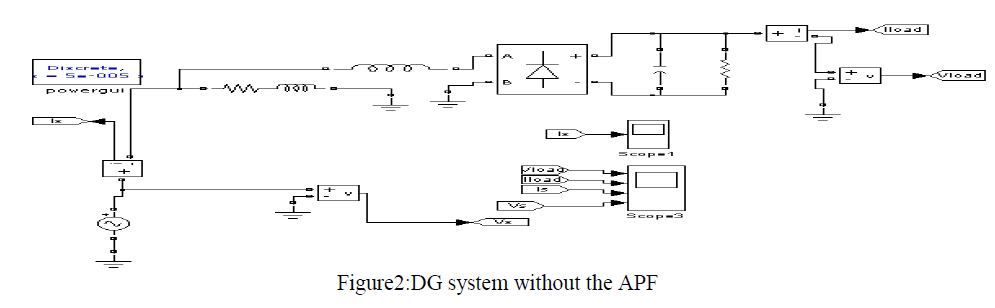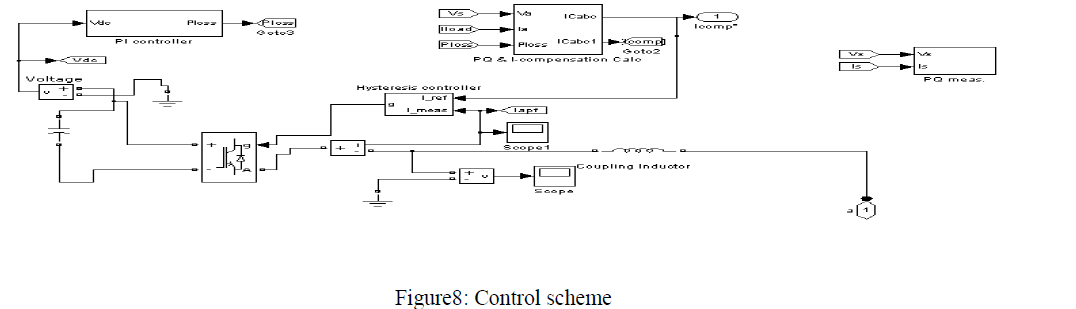The control scheme consists of Discrete PI controller with kp = 0.1,ki = 1 and Ploss is calculated. The gate pulses are generated using Hysteresis controller whose inputs are Ref current which is compensated current and APF current as shown in equation(6).Active and reactive powers are calculated using equations(2),(3).Vsource is same as without APF and other results are as shown below:

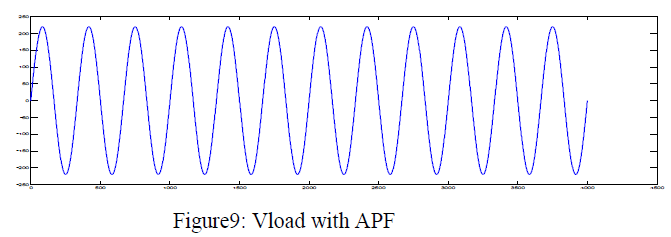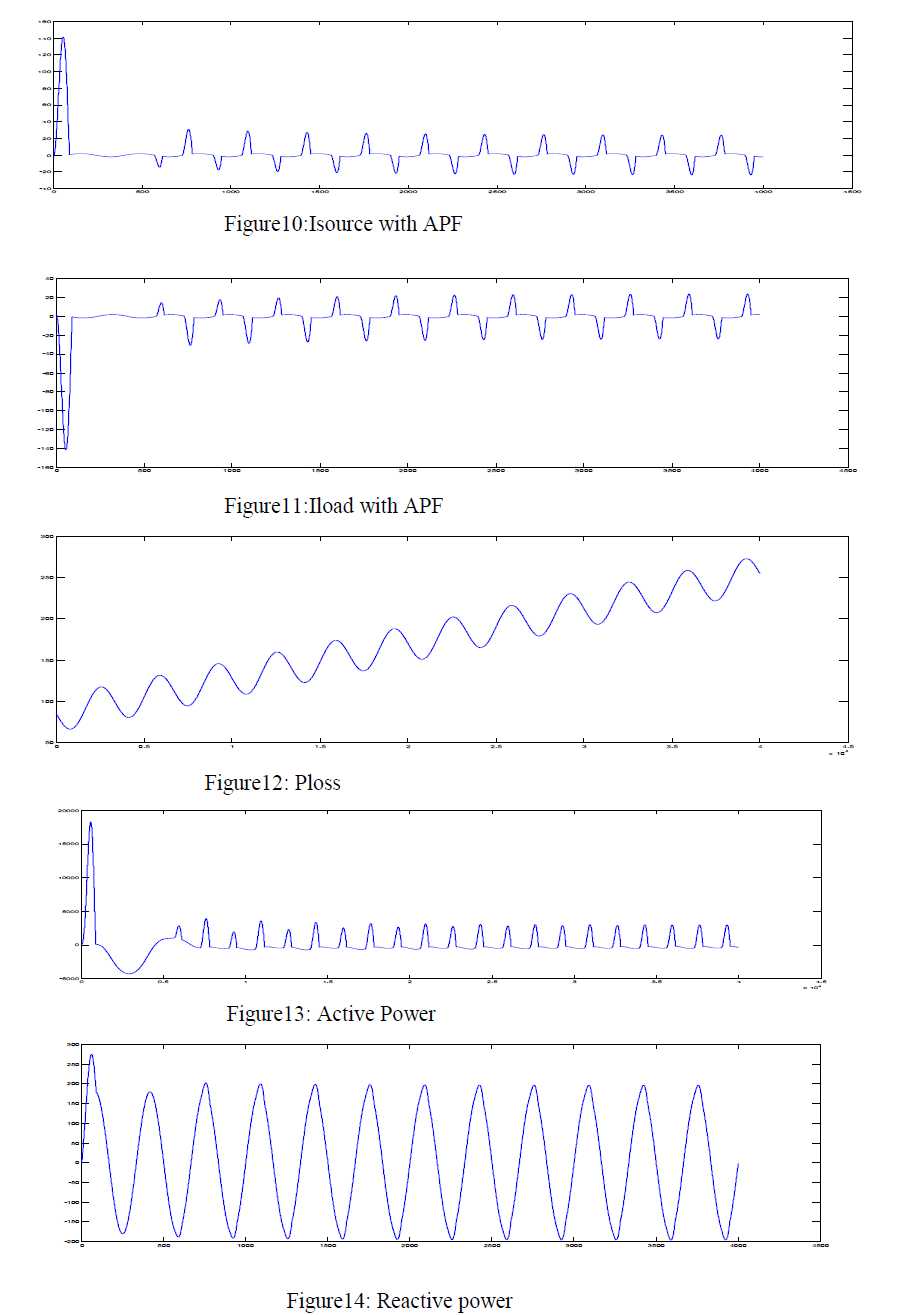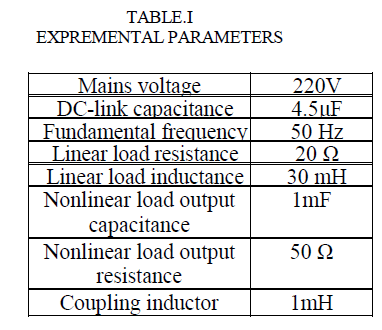
The figures9, 10,11,12,13, 14 shows that the grid-connected single-phase inverter injects active power into the grid and is able to compensate the local load reactive power and also the local load current harmonics. Reactive power is in hundreds and active power is in thousands. The parameters of the system are in the table1 as shown below:

VI. CONCLUSIONS

This paper deals with a single-phase APF for DG systems, requiring power quality features as harmonic and reactive power compensation for grid-connected operation. The proposed control scheme employs a control scheme based on the usage of only one LPfilter. The grid-connected single-phase inverter injects active power into the grid and is able to compensate the local load reactive power and also the local load current harmonics. Results have been obtained by simulation/MATLAB which include active power generation, load reactive power compensation, and load current harmonic compensation.The integration of power quality features has the drawback that the inverter will also deliver the harmonic compensation current with the direct consequence of increase the inverter overall current and cost. A current limitation strategy should be implemented current margin, this can be used for the compensation of reactive power and nonlinear load current harmonics. If the inverter output current exceeds the switch rating, then the supplied harmonic current must be reduced. An analysis of the inverter design that takes into account the current required for reactive power and current harmonics compensation is beyond the paper scope and it will be subject of future study.

References

T. E. McDermott and R. C. Dugan, “Distributed generation impact on reliability and power quality indices,” in Proc. IEEE Rural Electr. Power Conf., 2002, pp. D3–D3_7.
Francisco De la Rosa, Harmonics and Power System, Taylor & Francis Group, 2006.
Metalect Corporation (2004), “Active Harmonic Compensator Unit”, http://www.metalect.co.nz/harmonic.htm
Bimal K. Bose, Power Electronics and Motor Drives, Elsevier Inc.2006.
Ali E., Abdolhosein N. and Stoyan B. Bekiarov, Uninterrutible Power Supplies and Active Filters, CRC Press LLC, 2005.
L. P. Kunjumuhammed and M. K. Mishra, “Comparison of single phase shunt active power filter algorithms,” in Proc. IEEE Power India Conf.,2006, pp. 8–15.
S. M. Silva, B. M. Lopes, B. J. C. Filho, R. P. Campana, and W. C. Bosventura, “Performance evaluation of PLL algorithms for single-phase grid connected systems,” in Proc. IEEE IAS Conf. Rec., 2004, pp. 2259–2263.
L. P. Kunjumuhammed and M. K. Mishra, “A control algorithm for singlephase active power filter under non-stiff voltage source,” IEEE Trans. Power Electron., vol. 21, no. 3, pp. 822–825, May 2006.
M. T. Haque, “Single-phase pq theory for active filters,” in Proc. IEEE TENCON Conf. Rec., 2002, pp. 1941–1944.
M. Saitou and T. Shimizu, “Generalized theory of instantaneous active and reactive powers in single-phase circuits based on Hilbert transform,” in Proc. IEEE PESC Conf. Rec., 2002, pp. 1419–1424.
M. Saitou, N. Matsui, and T. Shimizu, “A control strategy of single-phase active filter using a novel d–q transformation,” in Proc. IEEE IAS Conf. Rec., 2003, pp. 1222–1227.
M. Gonzalez,V. Cardenas, and F. Pazos, “DQ transformation development for single-phase systems to compensate harmonic distortion and reactive power,” in Proc. IEEE CIEP Conf. Rec., 2004, pp. 177–182.
S. M. Silva, B. M. Lopes, B. J. C. Filho, R. P. Campana, and W. C. Bosventura, “Performance evaluation of PLL algorithms for single-phase grid connected systems,” in Proc. IEEE IAS Conf. Rec., 2004, pp. 2259–2263.
L. R. Limongi, R. Bojoi, A. Tenconi, and L. Clotea, “Single-phase inverter with power quality features for distributed generation systems,” in Proc. IEEE OPTIM Conf. Rec., 2008, pp. 313–318.