Index Terms
|
| Distributed generator, economic dispatch, is-landed operation, microgrid, smart grid. |
NOMENCLATURE
|
 |
 |
INTRODUCTION
|
| E LECTRIC power systems have been undergoing profound changes in response to various needs, such as environmental compliance, energy conservation, better grid reliability, improved operational efficiency, and customer ser-vice [1]. “Smart grid,” “intelligent grid,” and “next-generation grid” are the names applied to the power grid of the future, in which the electrical infrastructures and intelligent information networks will be integrated in order to satisfy the aforementioned needs [1]–[4]. In the meantime, the increasing use of distributed energy resources (DERs), including intermittent renewable sources, will pose many challenges for the future grid, especially with regard to the distribution system [1]. In order to solve the interconnection problems of individual distributed generators (DGs), the concept of a microgrid has been proposed [5]–[7]. A microgrid is a low- or medium - voltage distribution network, comprising various DGs, storage devices, and controllable loads, which can be operated in either the grid- connected or islanded mode [5], [6]. To date, there have been numerous research projects on the design, control, and operation of micro grids throughout the world, such as the CERTS microgrid in USA [6], [7], the MICROGRID project of Europe [8], and the new energy integration test project carried |
| out by NEDO in Japan [9]. |
| In [8] and [10]–[13], a central controller and an energy man-agement system (EMS) were proposed as a means of deriving the greatest benefit from the operation of a microgrid, and in-creasing the efficiency of DG usage. The principal functions of a microgrid EMS are to provide power and voltage . |
| Among the above functions, this paper focuses on the problem of determining the power references of DGs for the optimal operation of a microgrid. The optimization of a micro-grid has important differences from the case of a large power system and its conventional economic dispatch (ED) problem [13]. One of the most important differences is the necessity for stable mode transition from a grid-connected to the islanded operation in case of grid faults. Therefore, we propose the formulations of the ED problem for micro grids and its related constraints, which yield the fuel cost minimization during the grid-connected operation while ensuring stable operation after islanding. |
| The remainder of this paper is divided into five sections. Section II introduces several issues regarding the power control of DGs in a microgrid. In Section III, the economic dispatch problem and related constraints are formulated for a microgrid. Section IV presents the formulation of the constraint for the stable islanded operation in accordance with the power-sharing principle between the DGs. Section V discusses the numerical simulation results which are utilized to investigate the effect of each constraint on the operational cost. Finally, Section VI contains some concluding remarks. |
TECHNICAL ISSUES RELATED TO MICROGRID ED
|
| A. Active Power and Frequency Control in a Microgrid |
| Before developing the formulation of the ED problem for a microgrid, we will brie fly discuss some technical issues related to the active power and frequency control of DGs: 1) the power-control mode, 2) the power-sharing principle among DGs during microgrid islanding, and 3) the controllability of energy sources. |
| 1) Power-Control Mode: The power output of a DG can be controlled by one of two different modes: unit output power control (UPC) or feeder flow control (FFC) [7]. A UPC-mode DG generates constant active power according to the power ref-erence, while the output of an FFC-mode DG is controlled so that the active power flow in the feeder remains constant. In this study, the power output reference for a UPC-mode DG and the feeder flow reference for an FFC-mode DG are determined by solving the ED problem regarding the optimal operation of a microgrid. |
| 2) Power-Sharing Principle During Microgrid Islanding: |
| When a microgrid is disconnected from the main grid, DGs must take the place of the main grid in matching the power demand. In many studies, power versus frequency droop control has been adopted in order to ensure that the power demand is dynamically balanced by the DGs [5]–[8]. Conventionally, the droop constant of a DG is considered to be a fixed parameter, determined so that the load demand is shared among DGs in proportion to their rated capacities. In nd [15], a new power-sharing principle is proposed in which the droop constants are periodically modified according to the operating points of the DG units. With this method, the DGs share power according to their operational reserves, rather than their capacities. We refer to the former techniques as fixed droop and the latter techniques as adjustable droop, and formulate the constraint related to the islanded operation of a microgrid in accordance with the power-sharing principle. |
| 3) Controllability of Energy Sources: The emerging gener-ation technologies suitable for microgrid application, together |
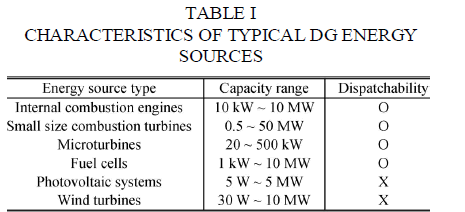 |
| With their typical capacity ranges, are listed in Table I [16]. Since most DGs are interfaced with the grid through an in-verter, they have various control capabilities, including power, frequency, and voltage control. However, the power outputs of DGs with renewable energy sources, such as photovoltaic cells and wind turbines, are driven by weather, not by system loads [7]. Therefore, these intermittent sources cannot be used as dis-patchable sources. In the ED problem, these sources will be treated as negative loads, and their power outputs will be as-sumed to be predictable within some range of uncertainty. |
| B. Constraints Associated With Microgrid Operation |
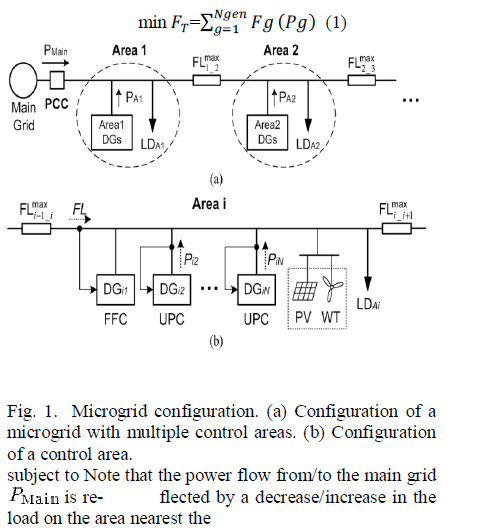
| As Fig. 1 indicates, the microgrid configuration considered in this study is a multiple-FFC configuration which is most suit-able for a microgrid in which none of the DGs are dominant [17], [18]. We assume that the variation of loads and the power out-puts of nondispatch able DGs in each control area are compen-sated by the dispatchable DGs in the same area. To accomplish this, the fi rst DG in each area operates in the FFC mode, while the others operate in the UPC mode, as shown in Fig. 1(b). With this configuration, any variation within an area can be compen-sated by the FFC- mode DG, and the flow between two adja-cent areas remains unchanged over a predetermined time period [17]–[20]. This property is advantageous to system operators, since microgrids can be thought of as controllable subsystems. |
| The basic ED problem is extended to include the additional constraints related to the operation of a microgrid. The con-straints considered in this study are as follows: |
| i) Reserve for variation in load demand |
| ii) Reserve for variation in the power outputs of nondis- patchable DGs |
| iii) Flow limits between two adjacent areas |
| iv) Reserve for the stable islanded operation. |
| Since the first three constraints have already been adopted as part of the ED problem for conventional power systems, they are simply modified for application to a microgrid. The unique constraint, concerning the reserve for the stable islanded opera-tion, will be discussed in detail in Section IV. |
ED PROBLEM FORMULATION FOR A MICROGRID
|
| A. Formulation of the Basic ED Problem |
| In a power system, the primary objective of the ED is to min-imize the total generation cost FT , while satisfying the power balance and generation limits of the units [21], [22]. This can be formulated as follows: |
 |
 |
FORMULATION OF THE CONSTRAINT FOR THE STABLE
|
| sources are assumed to be predicted for every time interval. |
| ISLANDED OPERATION |
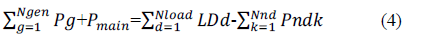 |
| Spinning Reserve Requirement Constraints: rmally |
| When a microgrid is islanded, the DGs will adjust ir power there areuncertainties involved in predicting and wind velocity and/or irradiance. Moreover, load demand in order to compensate for the loss of the main grid. Since the and the power outputs of intermittent sources usually vary system topology is radial, a power output change from any DG continuously. In order to compensate for these ariations, and will affect the power flow in the upstream lines. For example,to operate the system stably, additional reserve is necessary if power is imported from the main grid during the grid-con-and wind velocity and/or irradiance. Moreover, load demand nected operation, the DGs will increase their power outputs, and or a microgrid with the proposed configuration, in which all thus the upward flow in each line will be increased. Accord- the variations are picked up by the FFC-mode DG in each area, ingly if the power flow between two areas has remained near its the constraint can be formulated as 5) and (6). The spinning maximum limit during the grid-connected operation power reserve requirement is reflected as a decrease in the maximum cannot be transmitted during the transition, and this can limit Pmax and an increase in the minimum limit of make the system unstable the first DG within each area. In this study, it is assumed that In [8] and [23], load shedding algorithms have been proposed the load demand varies within r % of the predicted value, and for stable operation in case of such contingencies. However, in the power outputs of the non-dispatch able sources vary within this paper, we assume that the DGs are capable of supplying all of the predicted value loads without curtailment during the islanded operation. For this |
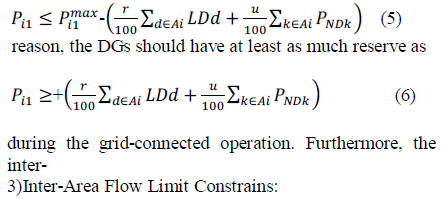 |
| the power flow between two adjacent areas is restricted by the power output reference of the DGs. The more the flow limit physical limits.This constraint can be formulated as (7)-(10) the more stable the system will be when islanded. How-ever, assuming that the number of areas in a feeder is n. such restriction will increase the operational cost during the grid-connected operation. |
| A. Constraint Formulation With Fixed Droop |
| With this power-sharing principle, each DG will change its power output in proportion to the inverse of the predetermined |
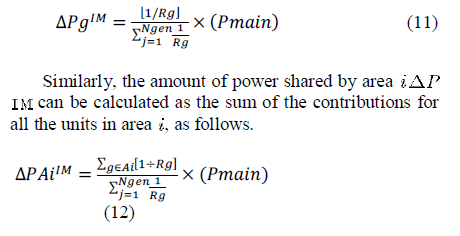 |
| The constraints can be formulated differently, depending on whether the power is initially imported from or exported to the main grid. |
 |
 |
| Since the DGs decrease their power outputs, the downward flow between areas will increase during the transition. There-fore, for the stable islanded operation without violating the physical inter - area flow limits, the downward flow should be maintained at an appropriate level below the limit during the grid-connected operation. The amount of additional flow from area i-1 to area is the sum of the power shared by the DGs in area and the areas downstream from it. Accordingly, the downward flow limit should be decreased by the amount of additional flow, whereas the upward flow limit remains unchanged. |
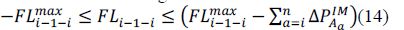 |
| 2) Power Initially Imported: If power is imported from the main grid during the grid-connected operation limit should also be refined I>0 |
| the DGs will increase their power outputs when the microgrid is disconnected from the main grid. Contrary to the former case, all DGs should have additional up spinning reserve, and the up-ward flow will be increased in the inter-area lines. Therefore, the |
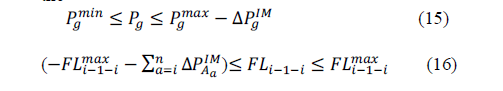 |
| Constraint Formulation With Adjustable Droop |
| When fixed droop is adopted, the contribution of each DG to the reserve is determined before solving the ED problem, and thus the output limit of a unit is modified according to (13) or (15) . However, when adjustable droop is applied, the power output reference for each DG is determined optimally, and the contribution to the reserve is then determined according to its operational margin [14], [15]. Hence, the output limits of the DGs do not need to be modified. The inter-area flow limits, on the other hand, should be refined as in the case of fixed droop. |
 |
| The download flow limits should be decreased in a manner similar to (14). However, in this case, since the power shared by each unit is unknown until the ED problem is solved, the de-creased value for the downward flow limits cannot be calculated directly as in the case of the fixed droop The downward power flow from area i-1 to area i during the grid-connected operation is the sum of the differences be-tweed the load demands and power outputs of area i and the areas downstream from it. |
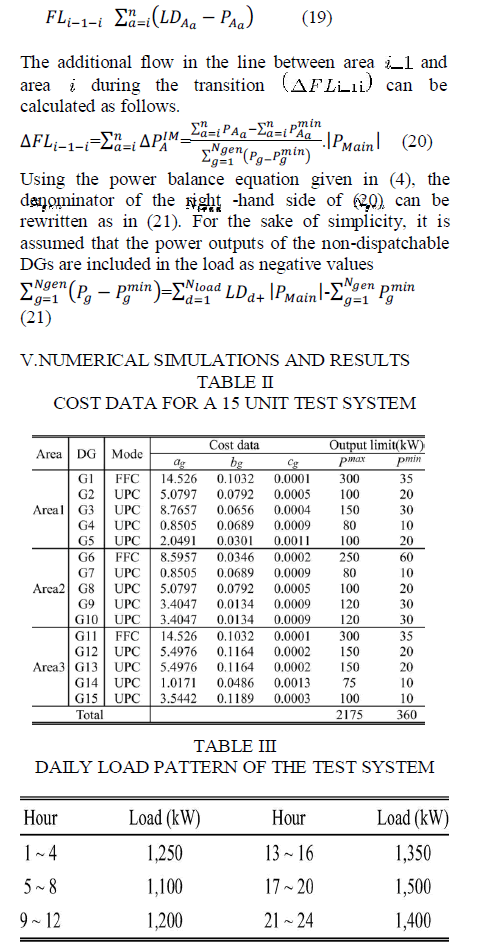 |
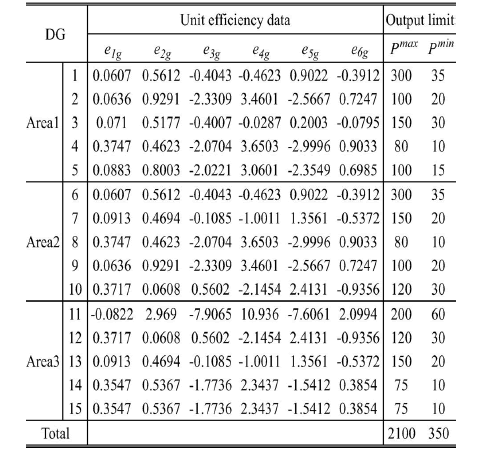
| A test system comprising three control areas is utilized for the analysis. We assume that five DGs are installed in each area; the cost data of the DGs and the daily load demands are summa-rized in Tables II and III, respectively. We also assume that the load demands in Table III include the effects of non-dispatch-able DGs, for simplicity. Since the effect of each constraint on the cost varies according to the load distribution, we tested two cases in regards to each condition. |
| Case 1) Load distribution factor of each area=0.35:0.25: |
| Case 2) Load distribution factor of each area=0.30:0.35: 0.35 |
| Various mathematical approaches and optimization tech-niques have been developed for solving ED problems. Chen proposed a direct search method (DSM) for and ED problem with transmission constraints [27], and applied it to ED prob-lems with various types of constraints, such as wind-thermal coordination dispatch and generation-reserve dispatch [28], [29]. In this study, the DSM is applied (with some modifica-tions) in order to solve the ED problem for microgrids, since it offers these definite advantages: i) the algorithm is straightforward and easy to implement, and ii) various inequality and equality constraints can be included. A multi-level conver-gence strategy, proposed in [27], is also used to improve the performance of the DSM. |
| B. Test 1: Inter-Area Flow Limit and Load Variation |
| The first simulation was designed to investigate the effect of the inter-area flow limit and the load variation on generation cost. To accomplish this, the total fuel cost was calculated under various conditions of load distribution, reserve requirement, and inter-area flow limit. The amount of power injected by the main grid,PMain , was assumed to be 0 in this test. The daily fuel costs in terms of the different conditions for the two cases are summarized in Fig. 2. |
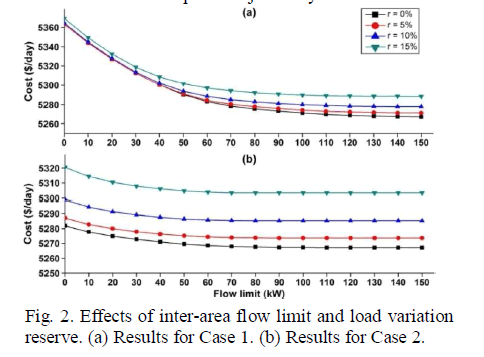 |
| The effects of both factors on cost can be summarized as fol-lows. Generation cost increased as the inter-area flow limit be-came smaller, and this occurred because units with higher in-cremental cost should increase their outputs as the flow limit decreases. In the test system, the DGs in area 2 had relatively lower incremental cost, but the load level of this area in Case 1 was only 25% of the total demand. Therefore, in order to re-duce the total generation cost, the DGs in area 2 should produce more power than the local load demand, and transfer the surplus power to other areas. For example, at a system load of 1500 kW, approximately 22 kW and 118 kW of power were transferred from area 2 to areas 1 and 3, respectively, when the inter-area flow was not limited. However, as the inter-area flow limit de-creases, the power transferred from area 2 is restricted, and the units in areas 1 and 3 with higher incremental cost should increase their outputs, which also increases the total generation cost. |
| We can also see that the cost showed a tendency to increase with the reserve requirement regarding load variation. The power output for the FFC-DGs in each area should be restricted in order to compensate for load variation, in accordance with (5) and (6). Since the incremental costs of the FFC DGs were relatively lower, an increase in the reserve requirement resulted in higher generation cost. Another observation from Fig. 2 is that the effect of the inter- area flow limit was dominant in Case 1, while the effect of load variation reserve was critical in Case 2. |
| C. Test 2: Reserve for the Stable Islanded Operation |
 |
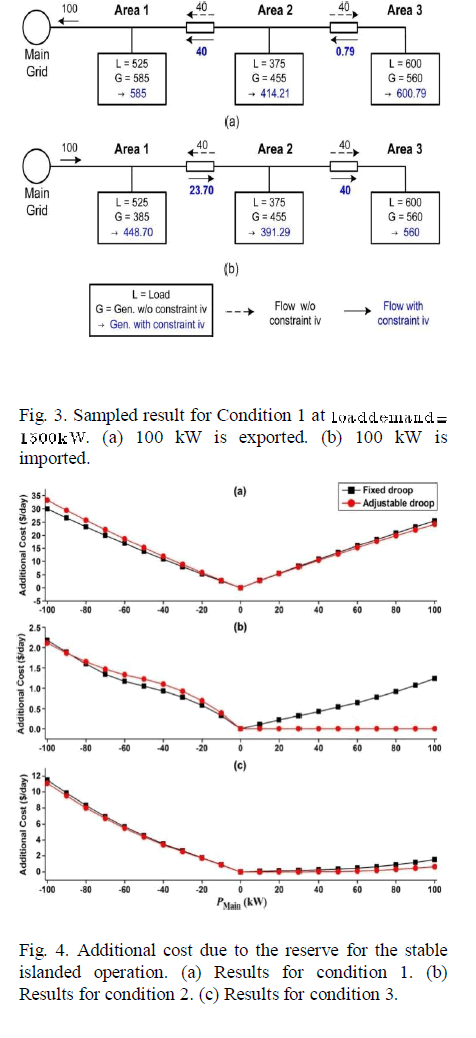 |
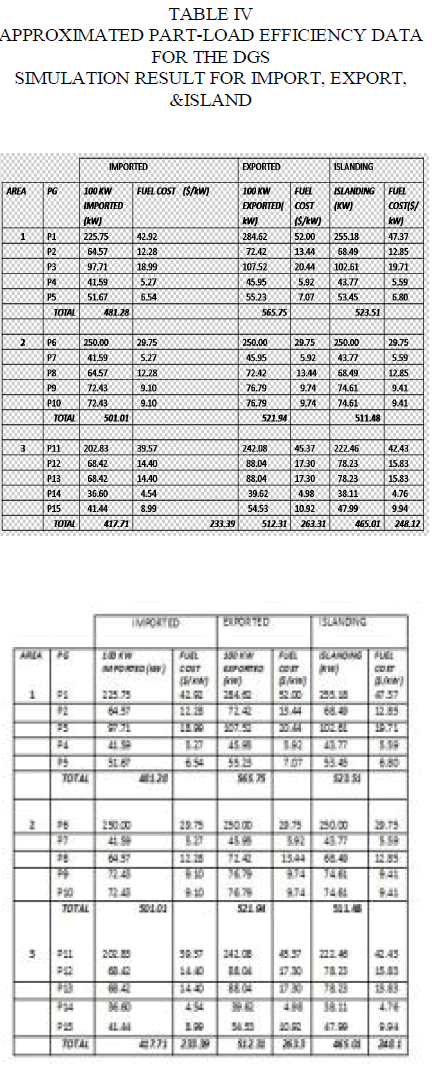 |
 |
CONCLUSION
|
| The economic dispatch problem was formulated in accor-dance with various constraints related to the operation of a microgrid. Some constraints were formulated by modifying ex-isting constraints to fit the configuration of a microgrid. We proposed an additional constraint to ensure the stable islanded operation of a microgrid, and provided a detailed formulation according to the power -sharing principle regarding the DGs. A test system with 15 DG units was developed for numerical simula-tions, taking into account the source type and part-load perfor-mance of each DG. We then investigated the effect of various parameters (including reserve requirement for the load varia-tion, flow limit, load distribution pattern, and the power injected by the main grid) on the cost. Although the cost increased by up to 0.7%, a microgrid could be operated economically during the grid-connected mode, and soundly during the islanded mode, using the modified dispatch solution, which takes into account the additional con |
References
|
- Ipakchi and F. Albuyeh, “Grid of the future,” IEEE Power Energy Mag., vol. 7, no. 2, pp. 52–62, Mar. 2009.
- J. D. Mcdonald, “The next-generation grid,” IEEE Power Energy Mag., vol. 7, no. 2, pp. 26–94, Mar. 2009.
- J. Giri, D. Sun, and R. Avila-Rosales, “Wanted: A more intelligent grid,” IEEE Power Energy Mag., vol. 7, no. 2, pp. 34– 40, Mar. 2009.
- G. H. Riahy and M. Abedi, “Short term wind speed forecasting for wind turbine applications using linear prediction method,”Renewable Energy, vol. 33, pp. 35–41, 2008.
- F. Toshihisa and Y. Ryuichi, “Microgrid field test experiences in Japan,” in Proc. Power Eng. Soc. Gen. Meet., Montreal, QC, Canada, Jun. 2006.
- S. J. Ahn, “A new power sharing method for distributed generations in the next-generation grid,” Ph.D. dissertation, Seoul National University, Seoul, Korea, Aug. 2009
- K.-L. Nguyen, D. J. Won, S. J. Ahn, and I. Y. Chung, “Power sharing method for a grid connected microgrid with multiple distributed generators,”J. Electr. Eng. Technol., vol. 7, no. 4, pp. 459–467, Jul. 2012.
- B. Rampriya, K. Mahadevan, and S. Kannan, “Application of differ-ential evolution to dynamic economic dispatch problem with transmis-sion losses under various bidding strategies in electricity markets,” J. Electr. Eng. Technol., vol. 7, no. 5, pp. 681–688, Nov. 2012.
- A. M. Azmy and I. Erlich, “Online optimal management of PEM fuel cell using neural networks,” IEEE Trans. Power Del., vol. 20, no. 2, pp. 1051–1058, Apr. 2005
|