Keywords
|
| MWN, Network Coding, HEF, Global Encoding Vector, Traffic analysis, Privacy preservation. |
INTRODUCTION
|
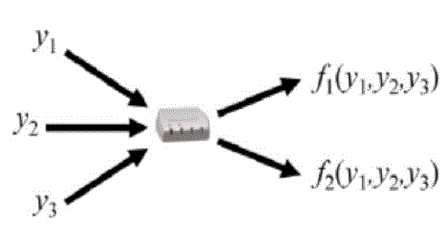
| What is network coding?[3] In simple words, in computer network environment consider a router which play role of intermediate node to transfer a data packet from source to sink. Each message on output link is a copy of the message which arrive earlier at input link of the intermediate node. Network coding, in contrast, allows each node in a network to perform some computation. Therefore, in network coding, each message sent on a node’s output link can be some function or “mixture” of messages that arrived earlier on the node’s input links, as illustrated in Figure 1. |
| Multi-hop Wireless Networks (MWNs) are regarded as promising solution for extending the radio coverage range of the existing wireless networks. System reliability can be improved through multi-path packet forwarding, which is feasible in MWNs. However, there exist many security and privacy issues in MWNs. such as eavesdropping, data modification/injection, and node compromising; these attacks may breach the security properties of MWNs, including confidentiality, integrity, and authenticity. Existing privacy preservation solutions, such as proxy-based schemes, Chaum’s mix-based schemes and onion-based schemes may either require a series of trusted forwarding proxies or result in severe performance degradation in practice, e.g., with an end-to-end delay of several minutes. Network coding was first introduced by Ahlswede et al [1]. Subsequently, two key techniques, random coding [2] and linear coding [1], further promote the development of network coding technologies. The random coding makes network coding more practical, while the linear coding is proven to be sufficient and computationally efficient for network coding. Currently, network coding has been widely recognized as a promising information dissemination approach to improving network performance. |
HOMOMORPHIC ENCRYPTION AND GEV’S
|
| Network coding has shown higher through put than conventional multicast theoretically and experimentally. A simple deployment of network coding can not prevent earliest decoding and traffic analysis since the explicit Global Encoding Vectors (GEVs, also known as tags) prefixed in the encoded packets provide a back door for adversaries to compromise the privacy of users. |
| In this paper, based on network coding and Homomorphic Encryption Functions (HEFs) [4], [6], we Propose a efficient privacy-preserving scheme for MWNs. This scheme offers following attractive features which are very helpful for the privacy preservation in MWN. |
| 1) Enhanced Privacy against flow tracing and traffic analysis: With the employment of HEFs, the confidentiality of GEVs is effectively guaranteed ,which makes it difficult for attackers to recover the GEVs. Even when some intermediate nodes are compromised, the adversaries still can not decrypt the GEVs, since only the sinks know the decryption key. The confidentiality of GEVs further brings the implicative benefit of the confidentiality of message content, because message decoding only relies on the GEVs. Moreover, with message recoding on encrypted GEVs, the coding/mixing feature of network coding can be exploited in a natural manner to satisfy the mixing requirements of privacy preservation against traffic analysis. |
| 2) Efficiency: Due to the Homomorphism of HEFs, message recoding at intermediate nodes can be directly performed on encrypted GEVs and encoded messages, without knowing the decryption keys or performing expensive decryption operations on each incoming packet. The performance evaluation on computational complexity demonstrates the efficiency of the proposed scheme. |
| 3) High Invertible GEVs: Random network coding is feasible only if the prefixed GEVs are invertible with a high probability. Theoretical analysis has proven that the influence the HEFs pose upon the invertible probability of GEVs is negligible. Thus, the random coding feature is kept in our network coding based privacy-preserving scheme. |
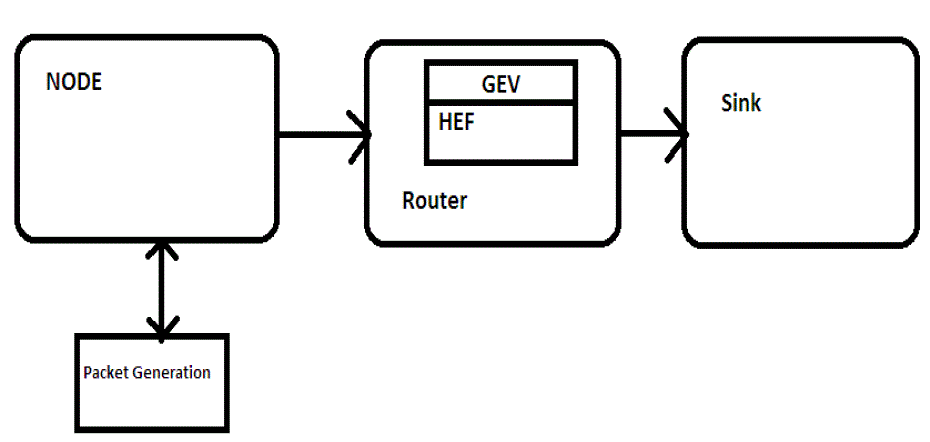
| Figure 2 shows the architecture of the scheme HEF operation performed at intermediate node on GEV |
| -Node:- Packet generation take place and tag are attached to packet and tagged packet is sent to the router where Encryption take palce. |
| -Router:- Tagged packet are encrypted using HEF operation and encrypted packet is sent to sink |
| - Sink:- Encrypted packet is decrypted using the public key of the sink and user can view the original information on log of the Sink. |
| A. Homomorphic Encryption Function: |
| Homomorphic Encryption Functions (HEFs) have the property of homomorphism, which means operations on plaintext can be performed by operating on corresponding cipher text. For example, suppose E(.) is a HEF. It is easy to compute E(x + y) from E(x) and E( y) without knowing the corresponding plaintext x and y. To be applicable in the proposed scheme, a HEF E(.) needs to satisfy the following |
| properties: |
| 1) Additivity: Given the cipher text, E(x) and E( y) , there exists a computationally efficient algorithm |
| Add() such that E(x + y) = Add(E(x), E( y)) . |
| 2) Scalar Multiplicativity: Given E(x) and a scalar t, there exists a computationally efficient algorithm |
| Mul() such that E(t . x) = Mul(E(x),t) . |
| B. Network Coding Model |
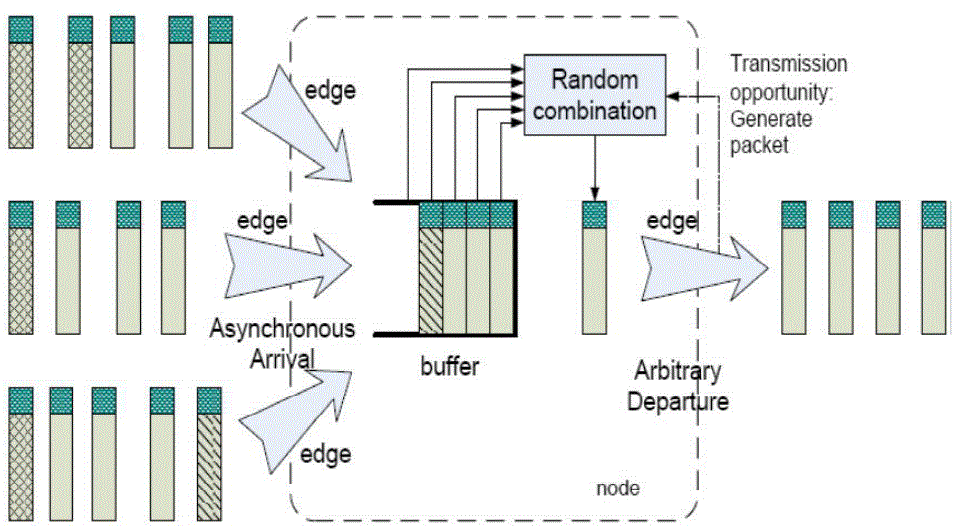
| Unlike traditional packet-forwarding systems, network coding allows intermediate nodes to perform computation on input messages, making output messages be the mixture of the input ones. This elegant principle implies a plethora of surprising opportunities, such as random coding [6]. As shown in Fig. 3, |
| whenever there is a transmission opportunity on an outgoing link, an outgoing packet is formed by taking a random combination of packets in the current buffer. An overview of network coding and possible applications has been given in [5], and packet tagging and buffering are key for practical network coding. Packet tagging will be introduced later. In practical network coding, source information should be divided into blocks with h packets in each block. All coded packets related to the kth block belong to generation k and random coding is only performed among the packets in the same generation. Packets within a generation need to be synchronized by buffering for the purpose of network coding at intermediate nodes. |
| C. Threat Model |
| We consider following two attacks, |
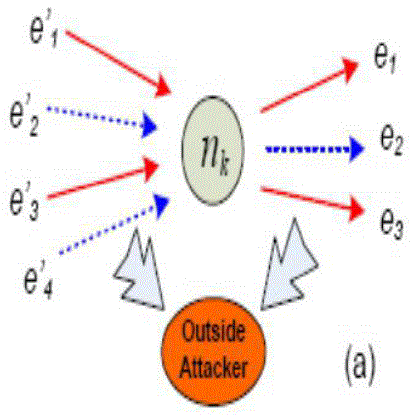
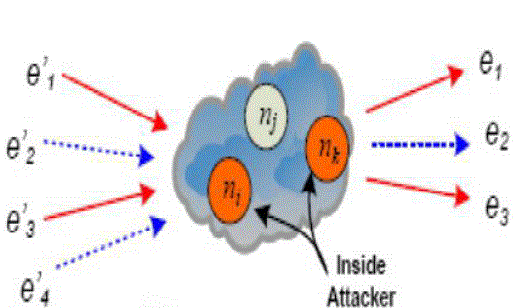
| Outside Attacker: An outside attacker can be considered as a global passive eavesdropper who has the ability to observe all network links, as shown in Fig. 4 (a). An outside attacker can examine the tags and message content, and thus link outgoing packets with incoming packets. Further, even if messages are encrypted in an end-to-end manner, it is still possible for a global outside attacker to trace packets by analysing and comparing the message cipher text. |
| Inside attacker: An inside attacker may compromise several intermediate nodes, as shown in Fig. 4 (b). Link-to-link encryption is vulnerable to inside attackers since they may already obtain the decryption keys and thus the message plaintext can be easily recovered. |
| Both inside and outside attackers may perform more advanced traffic analysis/flow tracing techniques, including size correlation, time-order correlation, and message content correlation [7]. Thus, adversaries can further explore these techniques to deduce the forwarding paths [5]. Without loss of generality, we assume that an anonymous secure routing protocol [3] is deployed to assist network nodes to determine the forwarding paths. The generation number of a packet can be hidden by the secure routing scheme so that an outside attacker cannot determine the generation of a packet for its further analysis. |
PROPOSED SCHEME FOR PRIAVACY PRESERVATION AGAINST TRAFFIC ANALYSIS
|
| Here we propose a novel network coding based privacy-preserving scheme for MWNs, which can efficiently thwart traffic analysis and flow tracing attacks. |
| Though providing an intrinsic mixing mechanism, the original network coding cannot provide privacy guarantee due to explicit GEVs, since an adversary can recover the original messages as long as enough packets are collected. Link-to-link encryption is vulnerable to inside attackers since they may already compromise several intermediate nodes and obtain the secret keys. An intuitive way to resolve this issue is to keep GEVs confidential to intermediate nodes by encrypting the GEVs in an end-to-end manner, which can prevent compromised intermediate nodes from analyzing GEVs or recovering the original messages. Such an intuitive approach, however, cannot prevent the adversaries from tracking the message cipher text since the “mixing” feature of network coding will be disabled by the end-to-end encryption. |
| To address this issue, in this paper, we employ the Paillier cryptosystem [5] as the HEF to apply encryption to GEVs. HEF can not only keep the confidentiality of GEVs, but also enable intermediate nodes to efficiently mix the coded messages. In the Paillier cryptosystem, given a message m and the public key (n, g), the encryption function is described as follows, |
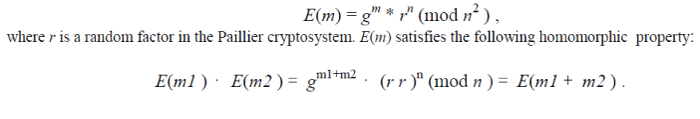 |
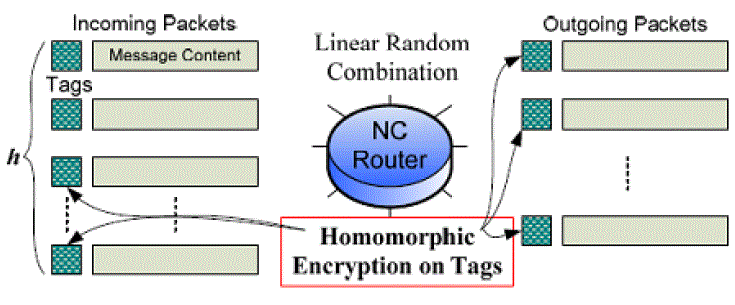
| With HEFs, intermediate nodes are allowed to directly perform linear coding/mixing operations on the coded messages and encrypted tags, as shown in Fig. 5. In other words, due to the homomorphism of the HEF, linear network coding can be achieved by operating on the encoded messages and the ciphertext of GEVs, without knowing the decryption keys or performing the decryption operations. The proposed scheme primarily consists of three phases: source encoding, intermediate random linear recoding, and sink decoding. Without loss of generality, we assume that each sink acquires two keys, the encryption key ek and the decryption key dk, from an offline Trust Authority (TA), and the encryption key ek is published to all other nodes. For supporting multicast, a group of sinks are required to obtain from the TA or negotiate the key pair in advance [6]; then, they can publish the encryption key and keep the decryption key private in the group. |
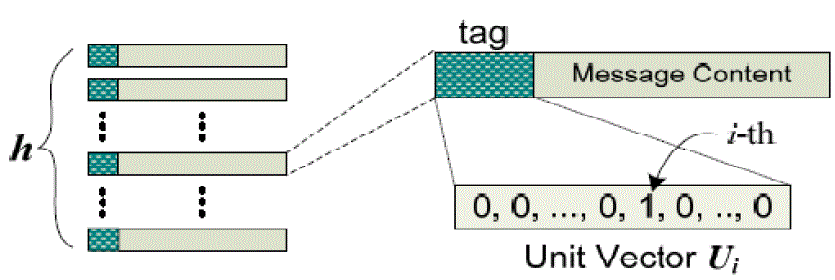
| Source Encoding: Consider that a source has h messages, say x1……xh , to be sent out. The source first prefixes h unit vectors to the h messages, respectively, as illustrated in Fig. 6. After tagging, the source can choose a random LEV and then perform a linear encoding operation on these messages. Thus one LEV will generate an encoded message with the GEV (which is equal to the LEV temporarily) tagged. |
| Intermediate Random Linear Recoding: After receiving a number of packets of the same generation, an intermediate node can perform random linear coding on these packets. To generate an outgoing packet, firstly, a random LEV [ β1 … βh] is chosen independently; then, a linear combination of message content of the incoming packets is computed as the message content of the outgoing packet, as shown in Fig. 3Since the tags of the h incoming packets are in cipher text format, and an intermediate node has no knowledge of the corresponding decryption keys, it is difficult for the intermediate node to perform functions such as earliest decoding to get the original message content. However, due to the homomorphism of the encryption function, a linear transformation can be directly performed on the encrypted tags of the incoming packets to generate a new tag for the outgoing packet, namely, linear transformation can be directly performed on the encrypted tags of the incoming packets to generate a new tag for the outgoing packet, namely, |
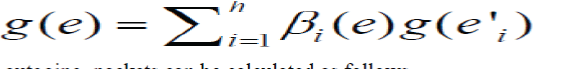 |
| the cipher text of the new GEVs for outgoing packets can be calculated as follows |
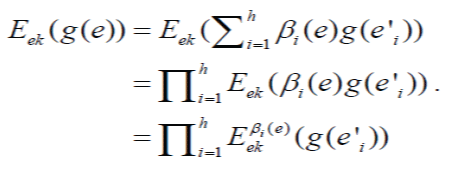 |
| The cipher text of new GEVs can be computed from the cipher text of GEVs of incoming packets without knowing the decryption key. Finally, the cipher text of a new GEV is prefixed to the corresponding message content to form a new outgoing packet, which is sent out to downstream nodes. |
| Sink Decoding: After receiving a packet, the sink first decrypts the packet tag using the corresponding decryption key dk. Once enough packets are received, a sink can decode the packets to get the original messages. Then, the sink derives the decoding vector, which is the inverse of the GEM, as shown in the following equations. |
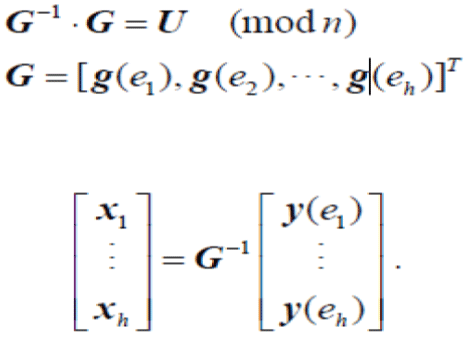 |
| Finally Sink can use the inverse the recover the original message. |
APPLICATION AND ADVANTAGES OF NETWORK CODING
|
| A. Applications Of Proposed Schemes: |
| 1) Consider a simple example of multicast communication in military ad hoc networks, where nodes can communicate with each other through multi hop packet forwarding. If an attacker can intercept packets and trace back to the source through traffic analysis, it may disclose some sensitive information such as the location of critical nodes (e.g., the commanders) and then further it may impair the location privacy. Subsequently, the attacker can take a series of actions to launch the so called Decapitation Strike to destroy these critical nodes |
| 2) Another example of event reporting in sensor networks . When a sensor detects an event, it sends a message including event related information to the base station. If an attacker (the hunter here) can intercept the message, it may know such sensitive information as whether, when and where a concerned event has happened, e.g., the appearance of an endangered animal in a monitoring sensor network . Following this, the attacker can take some action to capture/kill the animal. |
| 3) Wang et al. presented partial network coding (PNC) as a generic tool for continuous data collection. PNC generalizes the existing network coding (NC) paradigm but enables efficient storage replacement for continuous data, which is a major deficiency of the conventional NC. They proved that the performance of PNC is quite close to NC, except for a sub-linear overhead on storage and communication. |
| B. Advantages of Network coding |
| Advantage #1: Maximizing Throughput: Network coding has several advantages over routing. The first is the potential of network coding to improve throughput. Consider the following situation. Two streams of information, both at bit rate B bits per second, arrive at a node, contending for an output link, having capacity B bits per second. With network coding, it may be possible to increase throughput by pushing both streams through the bottleneck link at the same time. |
| Advantage #2: Minimizing Energy per Bit There are advantages to network coding beyond maximizing throughput. In particular, network coding can minimize the amount of energy required per packet (or other unit) of information multicast in a wireless network. |
| Advantage #3: Minimizing Delay Network coding can also minimize the delay, as measured, for example, by the maximum number of hops for a packet to reach a receiver. |
PERFORMANCE EVALUATION
|
Computational overhead:
|
| The computational overhead of the proposed scheme can be investigated respectively from three aspects: source encoding, intermediate recoding, and sink decoding. Since the computational overhead of the proposed scheme we will take the Paillier cryptosystem as the encryption method when necessary. Note that the computational overhead is counted independent of the underlying network coding framework. |
| Source Encoding Overhead: Consider h GEVs with h elements in each GEV, which form an h × h GEM. After source encoding, every element in the GEM is encrypted one by one. Thus, the computational overhead is O(?2) in terms of encryption operations. Every encryption operation requires 2 exponentiations, 1 multiplication, and 1 modulus operation in the Paillier cryptosystem. Therefore, the computational complexity is O(?2 ⋅ log n) in terms of multiplication operations. |
| Intermediate Recoding Overhead: In intermediate nodes, linear transformation on the elements of GEVs can be performed only by manipulating the cipher text of these elements because intermediate nodes have no knowledge of decryption keys. Thus, the computational complexity is O(h2 ⋅ log n) for a GEV and O(h3 ⋅ log n) for a GEM with h GEVs in terms of multiplication. |
| Sink Decoding Overhead: After receiving an encoded message, a sink can decrypt the elements in the GEV. According to the Paillier cryptosystem, decrypting an element requires1 exponentiation, 1 multiplication, and 1 division operation. Therefore, the computational complexity of decrypting a GEV is O(?⋅ log n ) in terms of multiplication operations. Thus, for a whole GEM with h GEVs, the computational overhead is O(h2 ⋅ log n ) in terms of multiplication. |
| Communication overhead: Let h messages be generated, and each message is of length ? bits. For source encoding, each message is prefixed with h code words from a ring of size ?. Considering the cipher text expansion of the Paillier cryptosystem, we can calculate the communication overhead as 2? ⋅ log n /l. |
| Performance optimization: As described in the previous subsections, the invertible probability and computational overhead of the proposed scheme are 1− p(p^-1 +q^-1) and O(?3 ⋅ log n ), respectively. Thus, the statistical computational overhead for a GEM can be expressed in terms of multiplications as follows: |
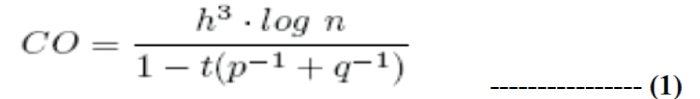 |
| From Eq(1)., we can see that the computational overhead of the proposed scheme is a monotonically increasing function of ?, i.e., the length of a GEV, for any given n and t. As discussed in Section IV, the security of the proposed scheme is also monotonically increasing with the increase of ?. Thus, a trade off between the security and the computational overhead should be considered in practical deployment. A typical way to deal with this trade off is to set the security requirements first and then choose the minimum ? to meet the requirements. In this way, the minimum computational overhead can be achieved. |
CONCLUSION AND FUTUREWORK
|
| In this paper we have proposed the a novel approach towards privacy preservation against traffic analysis In multi hop wireless network by implementing the homomorphic encryption function on global encoding vectors. The proposed scheme has two main significant features packet flow un traceability and message content confidentiality, which can efficiently protect the traffic analysis attack such as flow tracing In our future work we optimize the performance of proposed privacy preservation scheme because HEF become little in efficient when number GEV grows very much large in number . |
|
|
| |
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4a |
 |
 |
 |
| Figure 4b |
Figure 5 |
Figure 6 |
|
| |
References
|
- M. K. Reiter and A. D. Rubin, "Crowds: Anonymity for Web Transactions", ACM Trans. on Information and System Security, vol. 1, no. 1, pp. 66–92, Nov. 1998
- R. Ahlswede, N. Cai, S.-Y. R. Li, and R. W. Yeung, "Network Information Flow", IEEE Trans. on Information Theory, vol. 46, no. 4, pp. 1204-1216, Jul. 2000.
- M. Wang and B. Li, "Network Coding in Live Peer-to-Peer Streaming", IEEE Trans. On Multimedia, Vol. 9, No. 8, pp. 1554-1567, 2007
- Philip A. Chou and Yunnan Wu “Network coding for Internet and wireless network” June 2007 MSR-TR-2007-70
- P. Venkitasubramaniam and L. Tong, "Anonymous Networking with Minimum Latency in Multihop Networks", Proc.IEEE Symposium on Security and Privacy, pp. 18-32, 2008..
- Y. Fan, Y. Jiang, H. Zhu, and X. Shen, "An Efficient Privacy-Preserving Scheme against Traffic Analysis Attacks in Network Coding", Proc IEEE INFOCOM'09, Rio de Janeiro, Brazil, April 19-25, 2009.
- J. Dong, R. Curtmola, and C. Nita-Rotaru, “Secure network coding for wireless mesh networks: threats, challenges, and directions,” Computer Commun. (Elsevier), vol. 32, no. 17, pp. 1790-1801, Nov. 2009.
|