Keywords
|
| Data mining, classification, machine learning, privacy preservation. |
INTRODUCTION
|
| Data mining is a recently emerging field, connecting the three worlds of databases, statistics and artificial intelligence. Data mining is the process of extracting knowledge or pattern from large amount of data. It is widely used by researchers for science and business process. Data collected from information providers are important for pattern reorganization and decision making. The data collection process takes time and efforts hence sample datasets are sometime stored for reuse. However attacks are attempted to steal these sample datasets and private information may be leaked from these stolen datasets. Therefore privacy preserving data mining are developed to convert sensitive datasets into sanitized version in which private or sensitive information is hidden from unauthorized retrievers. |
| Privacy preserving data mining refers to the area of data mining that seeks to safeguard sensitive information from unsanctioned or unsolicited disclosure. Privacy preservation data mining was introducing to preserve the privacy during mining process to enable conventional data mining technique. Many privacy preservation approaches were developed to protect private information of sample dataset. |
RELATED WORKS
|
| In Privacy Preserving Data Mining: Models and Algorithms [14], Aggarwal and Yu classify privacy preserving data mining techniques, including data modification and cryptographic, statistical, query auditing and perturbation-based strategies. Statistical, query auditing and most cryptographic techniques are subjected beyond the focus of this paper. In this section, we explore the privacy preservation techniques for storage privacy attacks. |
| Data modification techniques maintain privacy by modifying attribute values of the sample data sets. Essentially, data sets are modified by eliminating or unifying uncommon elements among all data sets. These similar data sets act as masks for the others within the group because they cannot be distinguished from the others; every data set is loosely linked with a certain number of information providers. k-anonymity [15] is a data modification approach that aims to protect private information of the samples by generalizing attributes. K-anonymity trades privacy for utility. Further, this approach can be applied only after the entire data collection process has been completed. |
| Perturbation-based approaches attempt to achieve privacy protection by distorting information from the original data sets. The perturbed data sets still retain features of the originals so that they can be used to perform data mining directly or indirectly via data reconstruction. Random substitutions [16] is a perturbation approach that randomly substitutes the values of selected attributes to achieve privacy protection for those attributes, and then applies data reconstruction when these data sets are needed for data mining. Even though privacy of the selected attributes can be protected, the utility is not recoverable because the reconstructed data sets are random estimations of the originals. |
| Most cryptographic techniques are derived for secure multiparty computation, but only some of them are applicable to our scenario. To preserve private information, samples are encrypted by a function, f, (or a set of functions) with a key, k, (or a set of keys); meanwhile, original information can be reconstructed by applying a decryption function, f_1, (or a set of functions) with the key, k, which raises the security issues of the decryption function(s) and the key(s). Building meaningful decision trees needs encrypted data to either be decrypted or interpreted in its encrypted form. The (anti)monotone framework [17] is designed to preserve both the privacy and the utility of the sample data sets used for decision tree data mining. This method applies a series of encrypting functions to sanitize the samples and decrypts them correspondingly for building the decision tree. However, this approach raises the security concerns about the encrypting and decrypting functions. In addition to protecting the input data of the data mining process, this approach also protects the output data, i.e., the generated decision tree. Still, this output data can normally be considered sanitized because it constitutes an aggregated result and does not belong to any individual information provider. In addition, this approach does not work well for discrete-valued attributes. |
DECISION TREE CLASSIFIER
|
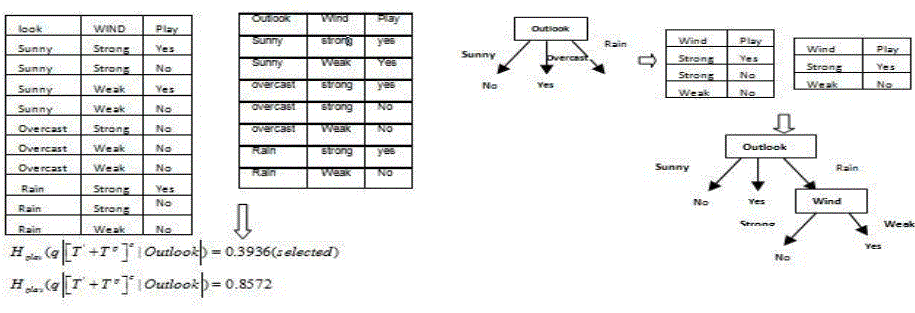
| A decision tree[3][4][5] is defined as “a predictive modeling technique from the field of machine learning and statistics that builds a simple tree-like structure to model the underlying pattern of data”. Decision tree is one of the popular methods is able to handle both categorical and numerical data and perform classification with less computation. Decision trees are often easier to interpret. Decision tree is a classifier which is a directed tree with a node having no incoming edges called root. All the nodes except root have exactly one incoming edge. Each non-leaf node called internal node or splitting node contains a decision and most appropriate target value assigned to one class is represented by leaf node. Decision tree classifier is able to break down a complex decision making process into collection of simpler decision. The complex decision is subdivided into simpler decision on the basis of splitting criteria. It divides whole training set into smaller subsets. Information gain, gain ratio, gini index are three basic splitting criteria to select attribute as a splitting point. Decision trees can be built from historical data they are often used for explanatory analysis as well as a form of supervision learning. The algorithm is designed in such a way that it works on all the data that is available and as perfect as possible. According to Breiman et al. [6] the tree complexity has a crucial effect on its accuracy performance. The tree complexity is explicitly controlled by the pruning method employed and the stopping criteria used. Usually, the tree complexity is measured by one of the following metrics: |
| • The total number of nodes; |
| • Total number of leaves; |
| • Tree depth; |
| • Number of attributes used. |
| Decision tree induction is closely related to rule induction. Each path from the root of a decision tree to one of its leaves can be transformed into a rule simply by conjoining the tests along the path to form the antecedent part, and taking the leaf’s class prediction as the class value. The resulting rule set can then be simplified to improve its accuracy and comprehensibility to a human user [7]. |
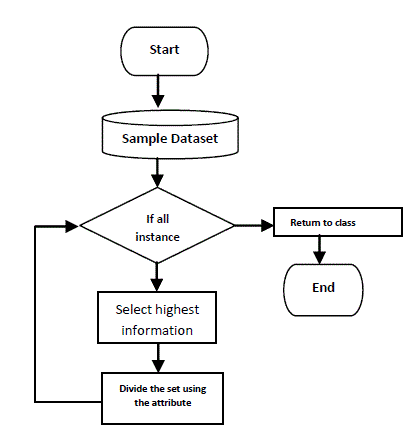
| Flowchart for tree based classification is shown in fig.1 |
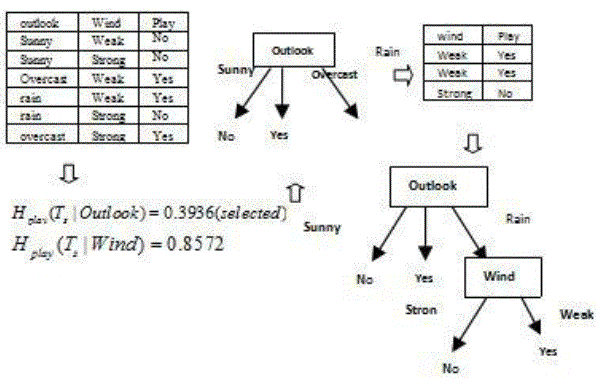
| Hyafil and Rivest proved that getting the optimal tree is NP-complete [8]. Most algorithms employ the greedy search and the divide-and-conquer approach to grow a tree. In particular, the training data set continues to be split in small. The related algorithm ID3 and C4.5 [9] adopt a greedy approach in which decision trees are constructed in top down recursive divide and conquer manner. ID3 was one of the first Decision tree algorithms. It works on wide variety of problems in both academia and industry and has been modified improved and borrowed from many times over. ID3 picks splitting value and predicators on the basis of gain in information that the split or splits provide. Gain represents difference between the amount of information that is needed to correctly make a prediction both before and after the split has been made. Information gain is defined as the difference between the entropy of original segment and accumulated entropies of the resulting split segment. C4.5 is an extension of ID3, presented by the same author (Quinlan, 1993). It uses gain ratio as splitting criteria. |
| The splitting ceases when the number of instances to be split is below a certain threshold. C4.5 can handle numeric attributes. It performs error based pruning after growing phase. It can use corrected gain ratio induce from a training set that incorporates missing values. |
DATA SET COMPLEMENTATION APPROACH
|
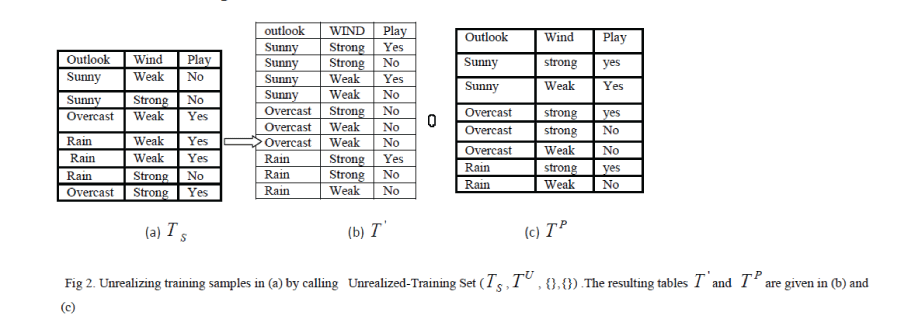
| Privacy preservation via dataset complementation is a data perturbed approach that substitutes each original dataset with an entire unreal dataset. Unlike privacy protection strategies, this new approach preserves the original accuracy of the training datasets without linking the perturbed datasets to the information providers. In other words, dataset complementation can preserve the privacy of individual records and yield accurate data mining results. However, this approach is designed for discrete-value classification only, such that ranged values must be defined for continuous values. |
 |
 |
 |
| If D2 T is a subset of D1 T , then all the elements existing in D2 T also exist in D1 T . Thus, the information content gained by classifying q-absolute-complement of a set of datasets, say D T , could be determined by using the size of U qT and the information of D T . |
| C. Unrealized Training Set |
| A training set S T is constructed by inserting sample data sets into a data table. However, a data set complementation approach, as presented in this paper requires an extra data table, P T . P T is a perturbing set that generated unreal data sets which are used for converting the sample data into unrealized training set, ' T . The algorithm for unrealized the training set, S T , as shown follows: |
 |
 |
DECISION TREE GENERATION
|
| The ID3 algorithm [18] build a decision tree by calling algorithm Choose-Attribute recursively. This algorithm selects a test attribute (with the smallest entropy) according to the information content of the training set S T . The information entropy functions are given as |
 |
ALGORITHM
|
 |
| 8. examples ← {element i s of examples with best= i v } |
| 9. m← MAJORITY-VALUES(example i s ) |
| 10. subtree ← GENERATE-DECISION-TREE (example i s , attributes ← best, m) |
| 11.add a branch to tree with lable i v subtree |
| 12. return tree |
| A. Information Entropy Determination |
 |
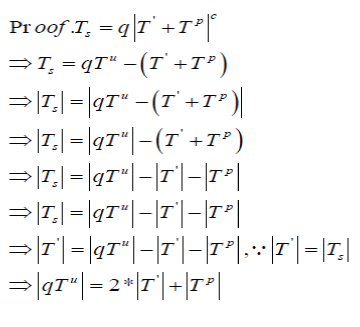 |
| B. Modified Decision Tree Generation Algorithm |
| As entropies of the original data sets, S T , can be determined by the retrieval information – the contents of unrealized training set, ' T , and perturbing set, P T , the decision tree of S T , can be generated by the following algorithm. |
 |
 |
 |
OUTPUT ACCURACY
|
| The decision tree generated from the unrealized samples is same as the decision tree, Tree S T , generated from the original sample by the regular method. |
| A. Storage Complexity |
| From the experiment, the storage requirement for the data set complementation approach increases from | S T | to s u (2T ?)* T , while the required storage may be doubled if the any attribute values technique is applied to double the sample domain. The best case happens when the samples are evenly distributed, as the storage requirement is the same as for the original. |
| B. Privacy Risk |
| The average privacy loss per leaked unrealized data set is small, except the even distribution case (in which the unrealized samples are the same as the originals). By doubling the samples domain, the average privacy loss for a single leaked data set is zero, as the unrealized samples are not linked to any information provider. The randomly picked tests show that the data set complementation approach eliminates the privacy risk for most cases and always improves privacy security significantly when new values are used in the attribute. |
CONCLUSION AND FUTURE WORKS
|
 |
| The data set complementation fails, if all training datasets were leaked, because the dataset reconstruction algorithm is generic. Therefore, further research is required to eliminate this limitation. This paper is implemented by using the ID3 decision tree algorithm and discrete values attributes. The further research should be develop by using the C4.5 decision tree algorithm with discrete value and continues value attributes. Future research should also explore means to reduce the storage requirement associated with the derived dataset complementation approach. This paper relies on theoretical proofs with limited practical tests, so testing with real samples should be the next step to gain solid ground on real-life application because the C4.5 decision tree algorithm is performed the numerical values. |
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
|
| |
References
|
- Agrawal, R., .and Srikant, R., Privacy-preserving data mining. In ACM SIGMOD International Conference on Management of Data, pages 439–450. ACM, 2000.
- Lindell, Y., and Pinkas. B., Privacy preserving data mining. In Advances in Cryptology, volume 1880 of Lecture Notes in Computer Science, pages 36–53. Springer-Verlag, 2000.
- Rokach L. and Maimon “Top-Down Induction of Decision Trees Classifiers – A Survey”, IEEE TRANSACTIONS ON SYSTEMS, MAN AND CYBERNETICS: PART C, VOL. 1, NO. 11, NOVEMBER 2002.
- Han, J., Micheline Kamber, “Data Mining: Concepts and Techniques”, Morgan Kaufmann, 2001.
- Rokach, L. , Maimon O. ,”Data Mining and Knowledge Discovery Handbook “,Second edition pages 167-192, Springer Science + Business Media,2010
- Breiman, L. , Friedman, J. , Olshen, R., and Stone. C. ,” Classification and Regression Trees”, Wadsworth Int. Group, 1984.
- Quinlan, J.R., “ Simplifying decision trees”, International Journal of Man- Machine Studies, 27, 221-234, 1987.
- Hyafil, L. and Rivest, R. L. , "Constructing Optimal Binary Decision Trees is {NP}-Complete," Inf. Process. Lett, vol. 5, pp. 15-17, 1976.
- Quinlan, J. R. , C4.5: Programs for Machine Learning. Morgan Kaufmann, 1993.
- Dowd, J., Xu, S. and Zhang, W., “Privacy-Preserving Decision Tree Mining Based on Random Substitions,” Proc. Int’l Conf. Emerging Trends in Information and Comm. Security (ETRICS ’06), pp. 145-159, 2006.
- Kargupta, H., Datta, S., Wang, Q., and Sivakumar, K., “On the privacy preserving properties of random data perturbation techniques”. In IEEE International Conference on Data Mining, 2003.
- Evfimievski, A. , Gehrke, J. , and Srikant, R.,” Limiting privacy breaching in privacy preserving data mining. In ACM Symposium on Principles of Database Systems”, pages 211–222. ACM, 2003.
- Aggrawal, S. , and. Haritsa, J. R,” A framework for high-accuracy privacypreserving mining”. In IEEE International Conference on Data Engineering, 2005.
- Kadampur, M. A, Somayajulu D.V.L.N., “A Noise Addition Scheme in Decision Tree for Privacy Preserving Data Mining”, Journal of Computing, Vol 2, Issue 1, January 2010, ISSN 2151-9617.
- Wang. L. L..,J.,, Zhang., J. ., ``Wavelet based data perturbation for simultaneous privacy preserving and statistics preserving.,'' In Proceedings of IEEE International Conference on Data Mining workshop., 2008.
- Aggrwal C. C..,Philip S Yu., “ Privacy preserving data mining models and Algorithms.”, Springer Science+Business media.,LLC..2008.
- Vaidya J. and Clifton, C., “Privacy-preserving decision trees over vertically partitioned data”. In Proceedings of the 19th Annual IFIP WG 11.3Working Conference on Data and Applications Security, Storrs,Connecticut, Springer , 2005.
- Liu, L., Kantarcioglu, M. , and Thuraisingham, B. , “Privacy Preserving Decision Tree Mining from Perturbed Data,” Proc. 42nd Hawaii Int’l Conf. System Sciences (HICSS ’09), 2009.
- Fong, P. K., and Jahnke, J. H. W. , “Privacy Preserving Decision Tree Learning Using Unrealized Data Sets” .” IEEE Transl. on knowledge and data engineering, vol. 24, no. 2, February2012.
|