Keywords
|
| Privacy Preserving; CART; decision tree. |
INTRODUCTION
|
| Collaboration is the important key to success. It brings mutual benefit and heavy results that helps organizations in decision making. But due to the concern of privacy of data, organization hesitates to collaborate. Now privacy preservation has been an important concern since distributed data mining came into scenario. Ever since the distributed database has entered, the three problems have occurred. First problem is privacy preservation of private data. Second problem is to run centralized data mining algorithm in distributed environment. Third problem is to extract efficient result after running the centralized data mining algorithm in a secured way. |
Data Mining
|
| Data mining [1] has been an important aspect in the industry due to huge availability of data. Data mining is best regarded as the result of natural development of information technology. Data mining often called knowledge discovery of data as it extract important knowledge from huge amount of data. As the technology changes so is the organization. Now a day’s organization uses distributed database. |
Distributed Database
|
| In this information age organization uses distributed database [2] because organization are geographically distributed. A distributed database is a collection of data which logically belongs to the same system but is distributed over the sites in a computer network. It is divided into three types. |
| Horizontal partitioning of database: Database is divided in such a way that databases D1 and D2 are the result of tuple sub division of a database D. |
| Vertical partitioning of database: Vertical database are the databases that are sub divided according to the attributes. Let a database D is of size n having an attributes is sub divided into databases D1 and D2 where D1 holding the attribute a1,a2,......,ak and D2 holding the attributes ak+1, ak+2,......,an. |
| Mixed partitioning of database: Here database is first horizontally partitioned then vertically partitioned or vice versa |
Classification Rule Mining
|
| Classification [3],[4] is a data mining or machine learning technique used to predict group membership for data instances. Classification rule mining is also called rule based classification. It uses IF-THEN RULES. The IF part of the rule is known as rule antecedent and the THEN part is known as rule consequent. These rules can be directly be mined from training set or indirectly by converting models and extracting the rule. |
Decision Tree Classifier
|
| It is a supervised learning method that constructs decision trees from training set data. Decision Tree Classifiers [3] are effectively used in areas like radar signal classification, character classification, medical diagnosis, experts system etc. A decision tree [1] is a flowchart like selection measures are used for the attribute that best partitions the tuples into different classes. During decision tree construction, many of the branches may reproduce noise or outliers in the training data. So tree pruning is done to improve the algorithm. It breaks the complex decision making process into a collection of simpler decisions. Decision tree algorithm has adopted greedy approach in which decision trees are constructed in top-down recursive divide-and-conquer manner. Most commonly used decision tree algorithms are Iterative Dichotomiser (ID3), C4.5 and CART. Privacy preserving decision tree algorithm has been used to solve distributed computation problem where the parties altogether build a decision tree over the data set by sharing the necessary data and preventing the exposure of private sensitive data. |
Privacy Preserving Techniques
|
| Privacy preserving has emerged data mining has emerged as a very active research area in data mining. Discovering knowledge through a combination of different databases raises security issue. Although data mining results usually do not violate privacy of individuals, it cannot be assured that an unauthorized person will not access the data is partitioned over different sites and data is not encrypted, it is impossible to derive new knowledge about the other sites. Data mining techniques try to identify regularities in data, which are unknown and hard to discover by individuals. Regularities or patterns are to be revealed over the entire data, rather than on individuals. However to find such disclosure of patters, the mining process has to access and use individual information. Techniques discussed in this paper are Scalar Product Protocol: The scalar product protocol[4] allows more than two parties for computation. The main goal of this protocol is to secure the private data of other parties such that a party can know its own result and data only. |
| X(lnX) Protocol: X(lnX) protocol[5],[6] is generally used for preserving privacy for two parties. Suppose we have two parties A and B having value Xa and Xb respectively. The goal of X(lnX) protocol is to give A and B both a share of Ya and Yb respectively such that |
| Ya + Yb = (Xa + Xb)ln(Xa + Xb) |
RELATED WORKS
|
| Classification [3], one of the machine learning techniques, has been a major breakthrough in data mining process that lead to decision tree. There are three most popular decision tree. First decision tree is ID3 [3] that uses information gain for attribute selection. Second decision tree is C4.5 [3] that uses gain ratio as its splitting attribute. Third decision tree is CART [7] that uses gini index as its splitting criteria. Privacy has been the major concern since the distributed database came into picture. Data mining classification algorithm uses centralized algorithm and are only used in centralized database. The main breakthrough was from Lindell and Pinkas [5] and Agrawal and Srikant [8]. Lindell and Pinkas have introduced secure multi party technique for classification using ID3 algorithm over horizontally partitioned dataset and showed the way in which how to classification algorithm can run in distributed database and preservation of privacy in private data has started from them. Through this path an extensive research on applying data mining classification technique in distributed database was conducted. To add more security Du and Zhan [4] has introduced a scalar protocol. Vaidya and Clifton in [9] and J. Vaidya [10] have introduced a secured way to apply ID3 classification algorithm in vertically partitioned database. Shen, Shao and yang [11] and Y. Shen, H. Shao, J. Jianzhong [12] studied C4.5 classification and introduced PPC4.5 algorithm over vertically distributed database for two parties. C4.5 algorithm has been extended to multiparty in vertically partitioned environment in [13]. In this paper we have designed privacy preserving CART over vertically distributed database. |
DATABASE MODEL
|
| The database is distributed over the sites are described below: There are N databases D1, ……,Dn distributed over n number of sites S1,……,Sn in such a way that if Di has j attributes then all database from D1,….. , Di-1 and from Di+1….. Dn have j attributes. |
PRIVACY PRESERVING DECISION TREE BUILDING
|
| The CART algorithm was proposed by Breiman, Friedman, Olshen and Stone in [7]. CART creates binary tree and uses Gini index as its splitting attributes. This makes CART different from other decision tree. In this paper Privacy preserving CART decision tree is generated using CART algorithm. |
Privacy Preserving Classification Problem
|
| Let us consider a scenario of two parties, A and B, wants to conduct classification technique. A has a private database Da and B has a private database Db. The two databases are union of both A and B as dataset [Da U Db] [4] and these two databases are joined vertically by putting Da and Db together so that the concentration of the jth record in Da with the jth record in Db becomes the jth record in [Da U Db]. The assumptions taken are Da and Db contains same number of data records. |
| Da contains some attribute for all records and Db contains the other attributes. |
| Both parties share class labels of all the records and also the names of all the attributes. |
Privacy Preserving CART Algorithm
|
| Let N maps the current node, D = Da U Db maps the current database. Nattr list maps the current test attributes |
| The PPCART Tree(D, Nattr list) Begin |
| STEP 1-Create root node R |
| A computes gini index for all attributes present in Da. Similarly B computes gini index for all attributes present in Db. Initialize the root with minimum gini index. Attribute of minimum gini index is selected as the attribute maximizes the impurity reduction. |
| STEP 2- If all records in D have same class value, and then return R as the leaf node with the specified class value Each record has been divided in between two parties and both parties share the class labels of all records. So if we want to determine whether the both parties remain with the same single class or not, we have to verify whether the records in Da or Db all belong to the same single class C or not. If they belong to the same single class, then returns the leaf node with that specific class value. |
| STEP 3-If Nattr list is empty or the left records are less than a given value then return R as a leaf node marked with the class value assigned to the most records in S. Both parties share the class labels of all records and the names of all attributes, so they both know whether Nattr list is null or not. If yes, just scan dataset Da or Db and statistic the most frequent class, marking the leaf with the most frequent class label. |
| STEP 4- A queue Q is initialized to contain the root node. |
| STEP 5- While queue Q is not empty do { |
| STEP 6- Pop out the first node N from Q. |
| STEP 7- Evaluate the gini index for each attribute. |
| STEP 8- Find the best split attribute. |
| STEP 9- If the split attribute is continual then find its partition value |
| STEP 10- Use the best split attribute to split node N into N1, N2 … Nn. |
| STEP 11-For i=1,......,n |
| { |
| If all records in Ni belong to the same class then return Ni as a leaf node marked with its class value |
| Else |
| add Ni to Q and go on executing the PPCART Tree (D, Nattr list) |
| } |
| } |
| STEP 12-Calculate the classified mistakes of each node and carry on the tree pruning. |
| End |
Computing the Best Split
|
| We need to calculate the gini index for each attribute to acknowledge the best splitting attribute. Let D represent the dataset belonging to the current node N. Let C represents the Needed dataset to compute the gini index for each record in the current satisfied node. There will have two kinds of situations: |
| If the attributes of C and the Nattr list belong to the same dataset, either of them can individually calculate gini index. If all the attributes involved in C and the _attr list do not belong to the same party, neither party can compute the information gain ratio by itself. In this case, everyone needs to union the other party to calculate it. The following three steps will be repeated until we get information gain ratio for all attributes. Finally we choose the attribute with the greatest value as a split attribute for the current node. |
| Computing L(D, Nattr list): L represents the logical expression that satisfies the current node N. L represents the logical expression that only involved in Da attributes. Lb represents the logical expression that only involved in Db’s attributes. |
| A scan dataset Da and produce a vector of size n. Va(i) = 1 if the ith record satisfies La else Va (i)=0. A may calculate the value of |
| v ector Va by itself. Similarly, B may also calculate the value of vector Vb. |
| Let Vi be a vector of size n, Vi(n)=1, if the nth record belongs to class i else Vi(k?=0. V (i)= Va (i) ? Vb (i) means the c orresponding record that satisfies both La and Lb. |
| S calar product Va Vb Va ( j) Vb ( j) means the number of record whichsatisfiesbothLa and Lb. |
| Pi Va (Vb V j ) (Va V j ) Vb means the number of belonging to class i in partition S. Now we can compute the gini index |
| L(D, Nattrlist) |
Computing Gain:
|
| ΔGain(D, N_attrlist) |
| G(s1 j s2 j ........ snj ) L(D, Nattrlist) |
| Where |
| L(D, N_attrlist) computes the gini index of each attributes G(s1j+s2j+……+snj) computes the gini index of the class values. |
| According to scalar product protocol [4] the semi-honest third party is introduced to compute the scalar product Va Vb without revealing privacy. The result is divided into two parts |
| Va Vb X a X b .Two parties X and Y respectively shares |
| XX and XY, which can guarantee that X cannot get the contents of Y and Y cannot get the contents of X, so it can preserve their privacy. |
| According to Xln(X) protocol [5], [6] we can obtain ln(XX+XY)=PX+PY. X and Y respectively shares PX and PY. (XX+XY) ln(XX+XY)=(XX+XY)(PX+PY)= XXPX+ XYPY+ XXPY+ XYPX where the result of XXPY is divided into two parts QX and QY respectively shared by X and Y. Similarly, the result of XYPX is also divided into two parts SX and SY, which is also respectively shared by X and Y. A can compute WX =XXPX + QX + SX and Y can compute WY =XYPY + QY + SY .So XX+XY ln(XX+XY) = WX+WY , the result is divided into two parts WX and WY ,and respectively shared by X and Y. |
| Let us consider a scenario where two parties X and Y want to conduct CART algorithm. Both parties share the class value (play). |
| Now both parties have their own private data and wishes the other party should not know their private data. So the problems occurred is to find the gini index and differential gini without the knowledge of second party. Let R be the requirement and it is divided into two subsets RX and RY where RX is the subset of requirement involving party X attributes and RY is the subset of requirement involving party |
| Y attributes. Let us consider two vector VX and VY are of size n respectively. VX(t)=1 and VY(t)=1 if tth record satisfies RX and RY respectively. else VX(t)=0 and VY(t)=0. Let us consider another vector VB to know if t attribute belong to a class C or not. If VB(C)=1 then attributes being to class C else VB(C)=0. V is a non zero entry where V(t)=VX(t) ? VY(t) (t=1,2,….,n) means V(t) is satisfying both RX and RY. Now party X and Y can compute their own private data by the following formulas For computing scalar product of VX and VY |
 |
| For computing PC which means calculating number of occurrences of class C in a partition p is |
| Pc VX (VY VC ) (VX VC ) VY |
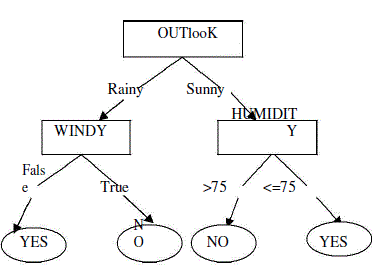
| For the computation of gini index party X has a vector VX and party Y has a vector VY both of size n. First the attribute “outlook” is computed. In outlook attribute there are three attributes “sunny”, “overcast”, “rainy”. As we know gini index makes binary splits so he have to combine the three attributes and the combination of attributes having minimum gini index is chosen as splitting attributes. So |
| TVX(outlook)(sunny,overcast)=(1,1,1,0,0,0,1,1.1.0,1,1,1,0)T VX(outlook) ((sunny,overcast)-no)=(1,1,0,0,0,0,0,1,0,0,0,0,0,0) |
| TVX(outlook) ((sunny,overcast)-yes)=(0,0,1,0,0,0,1,0,1,0,1,1,1,0) T Vx(outlook) (sunny,rainy)=(1,1,0,1,1,1,0,1,1,1,1,0,0,1) |
| VX(outlook) ((sunny,rainy)-no)=(1,1,0,0,0,1,0,1,0,0,0,0,0,1) T VX(outlook) ((sunny,rainy)- |
| yes)=(0,0,0,1,1,0,0,0,1,1,1,0,0,0) T |
| VX(outlook) (overcast,rainy)=(0,0,1,1,1,1,1,0,0,1,0,1,1,1) T VX(outlook) ((overcast,rainy)-no)=(0,0,0,0,0,1,0,0,0,0,0,0,0,1) T |
| VX(outlook) ((overcast,rainy)-yes)=(0,0,1,1,1,0,1,0,0,1,0,1,1,0) T Temparature attributes is divided by the group “>75” and “<=75” since gini index doest work in real numbers. So VX(temparature)(>75)=(1,1,1,0,0,0,0,0,0,0,0,0,1,0) T |
| VX(temparature)((>75)-no)=(1,1,0,0,0,0,0,0,0,0,0,0,0,0) T VX(temparature)((>75)-yes)=(0,0,1,0,0,0,0,0,0,0,0,0,1,0) T |
| VX(temparature)(<=75)=(0,0,0,1,1,1,1,1,1,1,1,0,0,1) T |
| VX(temparature)( (<=75)-no)=(0,0,0,0,0,1,0,1,0,0,0,0,0,1) T VX(temparature)( (<=75)-yes)=(0,0,0,1,1,0,1,0,1,1,1,1,0,0) T |
| Again humidity attribute contains real number data so it is also divided into “>75” and “<=75”. |
| VY(humidity)(>75)=(1,1,1,1,1,0,0,1,0,1,0,1,0,1) T VY(humidity)((>75)-no)=(1,1,0,0,0,0,0,1,0,0,0,0,0,1) T VY(humidity)((>75)- |
| yes)=(0,0,1,1,1,0,0,0,0,1,0,1,0,0) T VY(humidity)(<=75)=(0,0,0,0,0,1,1,0,1,0,1,0,1,0) T |
| VY(humidity)((<=75)-no)=(0,0,0,0,0,1,0,0,0,0,0,0,0,0) T VY(humidity)((<=75)-yes)=(0,0,0,0,0,0,1,0,1,0,1,0,1,0) T |
| For windy attribute |
| VY(windy)(false)=(1,0,1,1,1,0,0,1,1,1,0,0,1,0) T VY(windy)((false)-no)=(1,0,0,0,0,0,0,1,0,0,0,0,0,0) T |
| VY(windy)((false)-yes)=(0,0,1,1,1,0,0,0,1,1,0,0,1,0) T VY(windy)(true)=(0,1,0,0,0,1,1,0,0,0,1,1,0,1) T |
| VY(windy)((true)-no)=(0,1,0,0,0,1,0,0,0,0,1,1,0,0) T VY(windy)((true)-yes)=(0,0,0,0,0,0,1,0,0,0,1,1,0,0) T For class attribute V(play)(yes)=(0,0,1,1,1,0,1,0,1,1,1,1,1,0) T V(play)(no)=(1,1,0,0,0,1,0,1,0,0,0,0,0,1) T |
| The attribute having minimum gini index is selected as splitting point. So outlook (rainy, sunny) is selected as splitting point as GiniIndexoutlook(rainy, sunny) is the minimum among others. Party X and party Y exchange the information and it is concluded that attribute outlook with group rainy and sunny is selected as root node since it has least gini index. |
| Suppose let outlook be rainy and windy is false then party X will compute vector |
| VX(outlook)(rainy)=(0,0,0,1,1,1,0,0,0,1,0,0,0,1)T |
| VX(outlook)((rainy)-no)=(0,0,0,0,0,1,0,0,0,0,0,0,0,1)T |
| VX(outlook)((rainy)-yes)=(0,0,0,1,1,0,0,0,0,1,0,0,0,0)T Party Y will compute vector |
| VY(windy)(false)=(1,0,1,1,1,0,0,1,1,1,0,0,1,0) T |
| Both parties have to use scalar product protocol to calculate outlook=rainy and windy= false. But to add more security xlnx protocol is also used such that |
| (XX+XY) ln(XX+XY)=(XX+XY)(PX+PY)= XXPX+ XYPY+ XXPY+ XYPX |
| where the result of XXPY is divided into two parts QX and QY respectively shared by X and Y. |
| Similarly, the result of XYPX is also divided into two parts SX and SY, which is also respectively shared by X and Y. |
| A can compute WX =XXPX + QX + SX and Y can compute WY =XYPY + QY + SY .So XX+XY ln(XX+XY) = WX+WY , the result is divided into two parts WX and WY ,and respectively shared by X and Y |
EXPERIMENTATION AND RESULTS
|
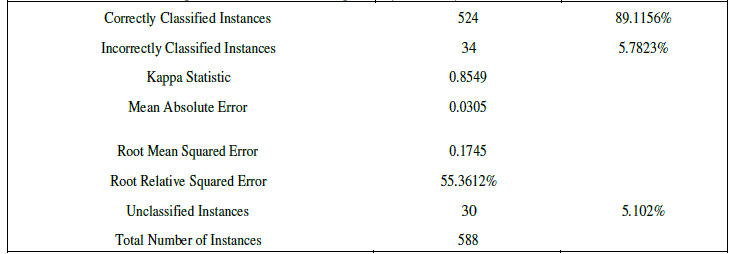
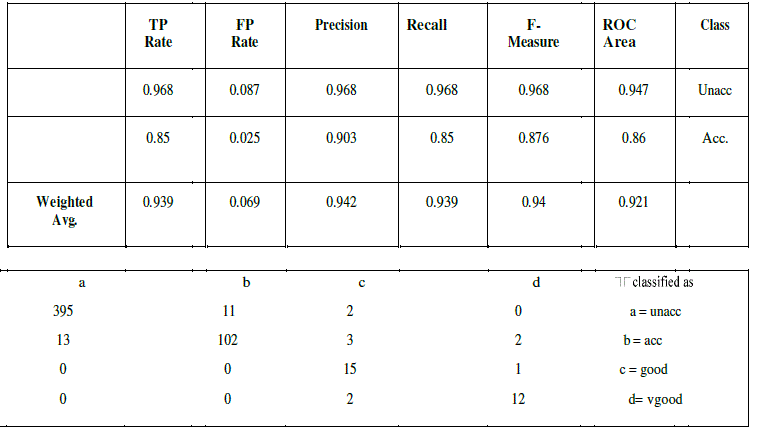
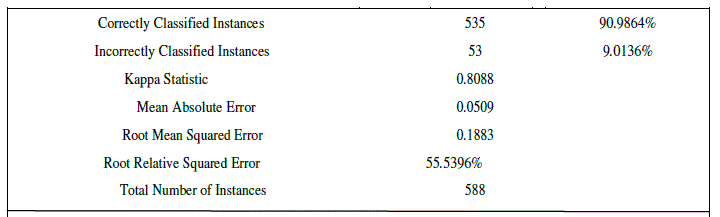
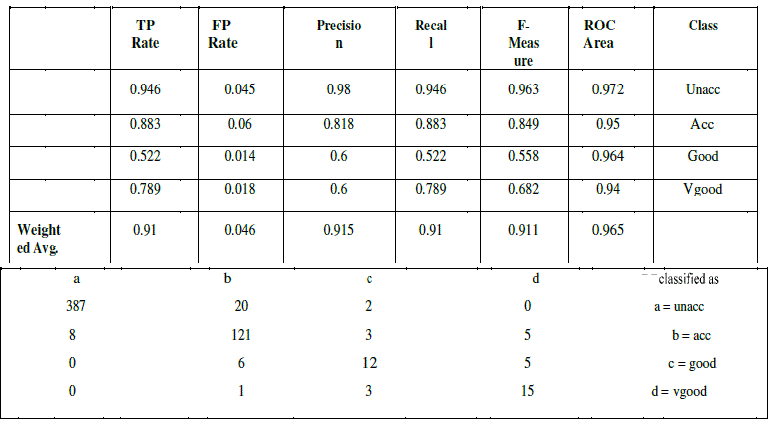
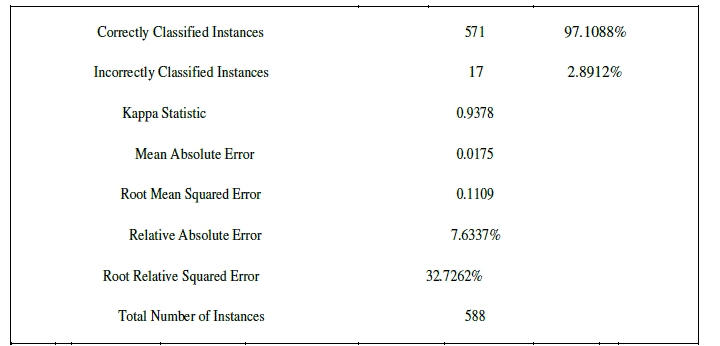
| CART uses gini index and construct binary tree that closely model more balanced splits. Moreover it is superior to ID3 and C4.5. To prove that Weka software tool is used. Weka is an open source data mining tool. A database of car evaluation was taken for comparison purpose among the three popular trees. The results of ID3 are shown below |
CONCLUSION AND FUTURE WORK
|
| This paper has showed the way for two parties to collaborate and use of CART decision tree algorithm which is better than other popular decision tree and closely model for balanced splits that brings heavy result to the party involved. Privacy of private data is fully preserved as privacy preserving protocol, that is, scalar product protocol is used. To add more security for preserving the privacy of private data, XlnX protocol is also used. So data leakage is zero.This tree can be used by different organizaion for accurate results. |
| |
Tables at a glance
|
 |
 |
| Table 1 |
Table 2 |
|
| |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
 |
 |
 |
| Figure 4 |
Figure 5 |
Figure 6 |
|
| |
References
|
- J. Han and M. Kamber, Data Mining: Concepts and Techniques, 2nd ed., Morgan Kaufmann , New York, Elsevier, 2009.
- S. Ceri and G. Pelagatti, Distributed Databases: Principles and Systems, Interntional Edition, Singapore, 1984.
- J. R. Quinlan, “Induction of decision trees,” Machine Learning, vol. 1, pp. 81–106, 1986.
- W. Du and Z. Zhan, “Building Decision Tree Classifier on Private Data,” in proc. IEEE International Conference on Privacy, Security and Data Mining, pp. 1-8. IEEE Press, Darlinghurst, 2002.
- Y. Lindell, B. Pinkas, “Privacy preserving data mining”, Advances in Cryptology-CRYPTO 2000, Lecture Notes in Computer Science Vol. 1880, pp 36-54, Aug. 2000.
- B. Pinkas, “Cryptographic Techniques for Privacy Preserving Data Mining,” SIGKDD Explorations, vol. 4, pp. 12-19, 2002.
- L. Breiman, J. Friedman, R. Olshen and C. Stone, Classification and Regression Trees, Wadsworth International Group, 1984.
- R. Agrawal, and R. Srikant, “Privacy-preserving data mining,” in proc. 2000 ACM SIGMOD on Management of Data, 2000, pp. 439–450.
- J. Vaidya, and C. Clifton, “Privacy preserving association rule mining in vertically partitioned data,” in proc. ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2002, pp 639-644.
- J. Vaidya, “Privacy Preserving Data Mining over Vertically Partitioned Data”, PhD thesis, Purdue University, 2004 Table V CART DETAILED ACCURACY BY CLASS
- Y. Shen, H. Shao, L. Yang, “Privacy Preserving C4.5 Algorithm over Vertically Distributed Datasets,” in proc. 2009 International Conference on Networks Security, Wireless Communications and Trusted Computing, 2009, pp 446-448.
- Y. Shen, H. Shao, J. Jianzhong, “Research on Privacy Preserving Distributed C4.5 Algorithm”, in proc. 2009 Third International Symposium on Intelligent Information Technology Application Workshops, 2009, pp 216-218.
- A. Gangrade, R. Patel, “Building Privacy-Preserving C4.5 Decision Tree Classifier on Multiparties”, International Journal on Computer Science
|