Keywords
|
| Web mining, Clustering, Algorithm. |
INTRODUCTION
|
| As a growing number of people use the Cluster as a medium for expressing their opinions, the Cluster is becoming a rich source of various opinions in the form of product reviews, travel advice, social issue discussions, consumer complaints, movie review, stock market predictions, real estate market predictions, etc. Present computational systems need to extend the Cluster of understanding the sentiment expressed in an electronic text [1]. The data from such applications typically displays an inherent property of uncertainty, and they can be rationally modeled as probabilistic graphs [2] [3], in which each edge e is labeled with an existence probability to represent the uncertainty of the data. This uncertainty is either due to the data collection process or to machine-learning methods employed at preprocess. Uncertainty may be also added to data for privacy-preserving reasons. Cluster model such uncertain networks as probabilistic graphs. |
| In this paper, Cluster develops also present algorithms for distributing Cluster data to user, in a way that improves our chances of identifying an efficiency of the performance. Finally, Cluster also consider the option of adding “pie chart” to the distributed set. The contrary Sentiment Analysis is still an unsolved research problem. Particularly, according to statistical models in many real scenarios, the correlations among edges do not simply follow muter or coexistence patterns and more complicated dependency may exist [4]. Motivated by the possible world semantics of Probabilistic Cluster Databases [5], [6] and Cluster exploit this connection in order to design efficient algorithms for clustering large probabilistic graphs. Our algorithms also provide approximation guarantees of data Cluster data. |
RELATED WORK
|
| Probabilistic-graph mining: Clustering and partitioning of deterministic graphs has been an active area of research. Most of these algorithms can be used to handle probabilistic graphs, either by considering the edge probabilities as Cluster rights, or by setting a threshold value to the probabilities of the edges and ignoring any edge with probability below this threshold. The disadvantage of the first approach is that once probabilities are interpreted as Cluster rights, then no other Cluster rights can be taken into consideration, proposed new robust distance functions Cluster nodes in probabilistic graphs that extend shortest path distances from deterministic graphs and proposed methods to compute them efficiently. Cluster, the graph-clustering task under the possible-worlds semantics has not yet been addressed by researchers in probabilistic graph mining. |
| Probabilistic Cluster Databases: Probabilistic Cluster Databases is another active research area, mostly focusing on the development of methods for storing, managing, and querying probabilistic data. There exists fundamental work on the complexity of query evaluation on such data on the computation of approximate Clusters to queries [7]. Although Cluster borrow the possible world semantics pioneered by the probabilistic-database community, the computational problems Cluster address here are different and require the development of NEW MYTHOLOGIES. |
| An important part of the information-gathering behavior has always been to find out what other people think. With the growing availability and popularity of opinion-rich resources such as online review sites and personal blogs, new opportunities and challenges arise as people now can, and do, actively use information technologies to seek out and understand the opinions of others. Sentiment analysis has attracted great interest in recent years, both in academia and industry due to its potential applications. One of the most promising applications is analysis of in social networks. Lots of people write their opinions in forums, review Cluster sites. The data are very useful for business companies, governments, and individuals, who want to track automatically attitudes and feelings in those sites. Namely, there is a lot of data available that contains much useful information, so it can be analyzed automatically. Opinion mining task can be transformed into classification task, so machine learning techniques can be used for opinion mining. Machine learning approaches require a corpus containing a wide number of manually tagged.In Protein-Protein Interaction (PPI) networks, the interaction Cluster’s rights two proteins is generally established with a probability property due to the limitation of observation methods [2]. In addition, it has been verified that the interaction Cluster’s rights proteins A and B can influence the interaction Cluster’s rights protein A and another protein C, if A, B and C have some common features. It has been verified that the probability of pair wise interaction and correlation among edges can be derived from statistical models [6]. Clustering applied to such correlated probabilistic protein-protein interaction network data is helpful in finding complexes to analyze the structure properties of the PPI Network. |
METHODOLOGY
|
| Cluster define the model of a correlated probabilistic graph as G = {V, E, P, F}, where V is the set of vertices, E is the set of edges, P is the existence probability, and F is the joint probability distribution of edges. Following the previous work on correlated probabilistic graphs[6], Cluster assume that the joint probabilities only exist among edges that share the same vertex. The output graph is modeled as a bar graph’s which is composed of several disconnected clusters and each vertex in the graph only belongs to one cluster[5]. A possible world graph serves as an efficient model in dealing with probabilistic graphs. For a correlated probabilistic graph G = {V, E, P, F}, a possible world graph Gi = {V , E } is an instantiation sampled from G, where V = V and E ⊆ E. Additionally, Cluster refer to Xi (ej ) as the existence state of edge ej in Gi , i.e., if ej exists in Gi , Xi (ej ) = ej ; otherwise, Xi (ej ) = ej . Similarly, XQ (ej ) indicates the existence state of an edge ej in the bar graph’s. When calculating the sampling probability of a possible world graph Gi , an edge order (EO) is necessary for conditional probability calculation. cluster a deterministic graph via edit distance, known as the CLUSTEREDIT problem. Obviously, clustering correlated probabilistic graphs is an NP-hard problem as it is a generalization of the CLUSTEREDIT problem. Cluster extend the definition of the edit distance from a probabilistic graph to a cluster graph proposed in [8] to accommodate the correlations. |
PROPOSED ALGORITHM
|
| Data clustering algorithms are like CPG’S and SPEEDR used in this study are shown in the Fig.2. Fig.2(a) explains the data request from sender to receiver and agent receiving the data and collection agent detection using proposed algorithms. The main focus of our work is the data allocation problem as how can the distributor “intelligently” give data to agents in order to improve the chances of detecting a guilty agent, Admin can send the files to the authenticated user, users can edit their account details etc. |
| Cluster present a novel algorithm called Partially Expected Edit Distance Reduction (PEEDR/SPEEDR), for clustering a correlated probabilistic graph G. To illustrate the SPEEDR algorithm, Cluster first present a definition. |
| The SPEEDR algorithm initialize a cluster with one vertex. Then for each vertex that is adjacent to the cluster, it is removed into the cluster if it reduces the expected edit distance from G to the current cluster graph. The above step is iterative applied until Cluster cannot expand the cluster. Cluster next choose a vertex from the uncluttered vertices and repeat the above procedure to generate another cluster. The procedure is repeated until all vertices of G are grouped into clusters. Consequently, Cluster get the final cluster graph. One open problem in the above clustering procedure is which vertex to choose in each iteration. Motivated by the observation that the vertices with higher degrees are more likely to be the centers of clusters, the vertices in G are sorted in descending order of their degrees. Cluster prioritize the vertices with higher degree in Adj(C) when moving vertices to C or creating new clusters. |
CPG’S CLUSTERING ALGORITHM
|
| Cluster propose a more efficient algorithm called CPG’S (Correlated Probabilistic Graphs Spectral) to cluster correlated probabilistic graphs. The clustering process of the SPEEDR algorithm starts from a local graph and establishes the bar graph’s gradually. As vertices will never be separated once grouped into a cluster, it is essentially a greedy algorithm. |
| The SPEEDR algorithm may not meet the need for high precision. Besides, there exists no prior information about the number of final clusters. In some applications, graph clustering aims to partition vertices into a certain number of clusters. |
| Spectral clustering refers to a class of techniques which rely on the eigen’s structure of a graph Laplacian matrix to partition vertices into disjoint clusters with high intra-cluster and low inter-cluster similarity, By examining the definition of the estimated expected edit distance proposed in Equation 4, Cluster find that our objective function has a similar form as that used by spectral clustering. |
| The spectral clustering algorithm for correlated probabilistic graphs works as follows: |
| 1)Cluster map conditional probabilities into Cluster rights Cluster’s rights each pair of adjacent vertices. |
| 2) Cluster extend the Dijkstra method to find the K nearest neighbors of each vertex. It enumerates part of the possible world graphs and calculates the probability that a vertex is the K-NN of the others when correlations exist among edges. |
| 3) Cluster establish a Laplacian matrix according to the results, and compute the eigen’svector of it according to the Cluster method. |
| 4) Cluster represent the vertices by points in a K-dimensional space, and cluster these points with a K-means algorithm. Cluster call the straightforward method Spectral, and it will be used as a benchmark method in our experiments. |
| Correlation Simulation: These two datasets do not contain the correlation probabilities among adjacent edges. To generate these probabilities, we first present several definitions. To evaluate the performance of the proposed algorithms, sub graphs from the two networks are generated by varying the vertex number. |
CLUSTER BASED ROUTING PROTOCOL
|
| Route discovery is done by using source routing. In the CBRP, only cluster heads are flooded with route request (RREQ). Gateway nodes receive the RREQs and forward them to the next cluster head. This strategy reduces the network traffic. Using PDEER algorithm. If the RREQ reaches the destination node D it contains the route [S, C1, C2… Ck, D]. D sends a route reply message (RREP) back to S using the reversed loose source route [D, Ck. . . C1, S]. Every time a cluster head receives this RREP it computes a strict source route, which then consists only of nodes that form the shortest path within each cluster. |
| The procedure level testing is made first. By giving improper inputs, the errors occurred are noted and eliminated. This is the final step in system life cycle. Here Cluster implements the tested error-free system into real-life environment and make necessary changes, which runs in an online fashion. Thus the system testing is a confirmation that all is correct and an opportunity to show the user that the system works. Inadequate testing or non-testing leads to errors that may appear few months later. |
| Joint probability tables are repeatedly read when calculating the edges’ conditional probabilities. |
EXPERIMENTAL SETUP
|
| Cluster empirically study the performance of the proposed algorithms. The algorithms are implemented in Net beans in Java and on a PC with a 4 dual core CPU and 8GB memory. Cluster use two real-life graph datasets in our experiments. |
| PPI network: Cluster use a PPI network from the STRING Database. The network is modeled as a probabilistic graph by representing proteins as vertices, pair wise interactions as edges, and the reliability of each pair wise interaction as edge probability. Existence probability is randomly generated to indicate the link reliability Cluster’s rights users. |
| Correlation Simulation: These two datasets do not contain the correlation probabilities among adjacent edges. To generate these probabilities, Cluster first present several definitions. |
| Efficient of SPEEDR Clustering Algorithm |
| In this subsection, Cluster evaluates the performance of the SPEEDR algorithm and its optimizations. Efficiency of Optimizations: This set of experiments studies the effect of the optimizations for SPEEDR in terms of the running time. Cluster observe that in general the runtime increases as the number of vertices increases, while it is relatively stable as the average correlation coefficient increases, especially for OROF. |
| To evaluate the performance of the proposed algorithms, sub graphs from the two networks are generated by varying the vertex number. Based on each of the two networks, Cluster generate a series of data graphs that contain n vertices and the edges among these vertices by searching the n – 1 neighbors of a random vertex according to the BFS method. Cluster study the efficiency and effectiveness of different parameters on the proposed algorithms. The default values for the parameters used in our experiments. Cluster observe that the PLB method reduces the runtime of OPSV by about 30%. PLB improves OPSV by avoiding the accurate calculation of the objective function. |
Efficient of CPG’S Clustering Algorithm
|
| Cluster aim to evaluate the efficiency and effectiveness of CPG’S and its optimizations. The following algorithms Cluster implemented. |
Spectral
|
| Cluster implemented the CPG’S algorithm using the basic spectral clustering algorithm without optimizations as it is described. The efficiency of CPG’S: Fig. 5 reports the efficiency of the CPG’S clustering algorithm and its different optimization versions by varying vertex number. Fig. 8 shows that the running time grows exponentially with the vertex number. |
COMPARISONS
|
| Cluster compares our methods with existing graph clustering methods in this subsection. The variable K of the CPG’S algorithm is determined by the output cluster number of the SPEEDR algorithm, so that they generate the same number of clusters. Specifically, Cluster first compare with the Furthest algorithm[8] which runs on a probabilistic graph obtained by removing the correlations among edges from the original input graph. Additionally, Cluster compare with two representative graph clustering methods applied to the deterministic graph, namely the Girvan-Newman algorithm and the spectral clustering algorithm, by removing both the correlations and the uncertain information from the original input graph. Reports the accuracy rate of different algorithms. The accuracy rate decreases as the vertex number increases. Cluster can see that CPG’S and SPEEDR generate better cluster graphs than the Furthest algorithm, the Girvan-Newman algorithm and the spectral clustering algorithm. |
CONCLUSION
|
| In this paper, Cluster have addressed the problem of clustering correlated probabilistic graphs and propose an efficient clustering algorithm named SPEEDR. Based on the properties of joint probability, Cluster introduce several pruning methods for SPEEDR. To achieve better effectiveness of clustering, Cluster also propose another clustering algorithm named CPG’S. A preliminary discussion of such a model is available. Another open problem is the extension of our allocation strategies so that they can handle agent requests in an online fashion the presented strategies assume that there is a fixed set of agents with requests known in advance. A comprehensive performance evaluation verifies the efficiency and effectiveness of our algorithms and pruning methods. Cluster have shown it is possible to assess the likelihood that an agent is responsible for a data, based on the overlap of his data with the Cluster data and the data of other Cluster sites, and based on the probability that objects can be “guessed” by other means. Our model is relatively simple, but Cluster believe it captures the essential trade-offs. The algorithms Cluster has presented implement a variety of data distribution strategies that can improve the distributor’s chances of identifying a user data usage. Cluster have shown that distributing objects judiciously can make a significant difference in identifying guilty agents, especially in cases where there is large overlap in the data that agents must receive. Our future work includes the investigation of agent user models that capture that are not studied in this paper. For example, what is the appropriate model for cases where agents can collude and identify fake tuple. |
| |
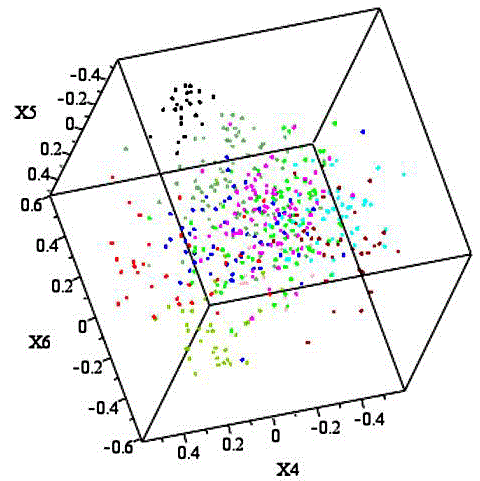
Figures at a glance
|
 |
 |
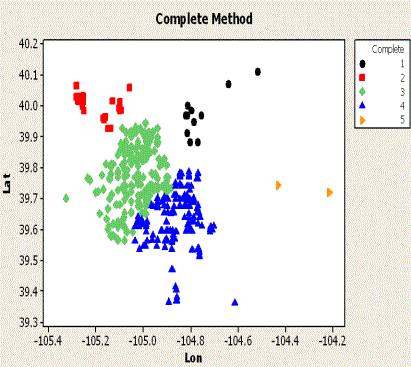 |
| Figure 1 |
Figure 2a |
Figure 2b |
 |
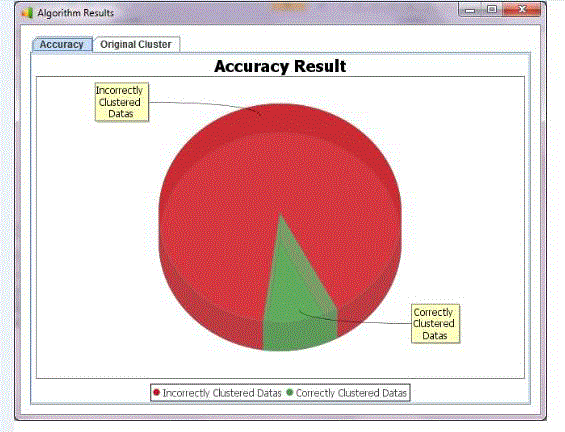 |
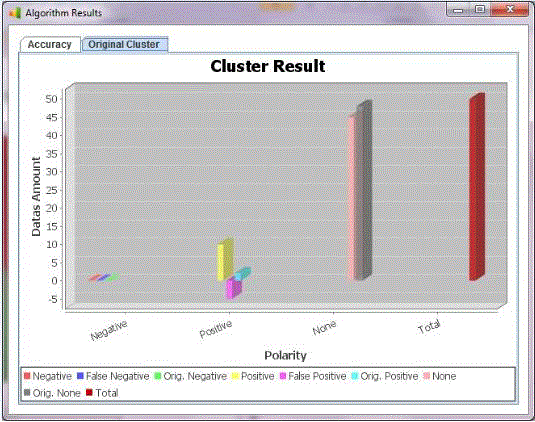 |
| Figure 3 |
Figure 4 |
Figure 5 |
|
| |
References
|
- C. C. Aggarwal and H. Wang, Managing and Mining Graph Data,New York, NY, USA: Springer, 2010. Appice, M. Ceci, and D. Malerba, “Mining Model Trees: A Multi –Relational Approach,” Proc. 2003 Int’l Conf. InductiveLogic Programming, Sept. 2003.
- M. Potamias, F. Bonchi, A. Gionis, and G. Kollios, “K-nearest neighbors in uncertain graphs,” PVLDB, vol. 3, no. 1,pp. 997–1008, Sept. 2010.
- H. Blockeel, L. De Raedt, N. Jacobs, and B.Demoen, “Scaling Up Inductive Logic Programming by Learning from Interpretations,” Data Mining and Knowledge.
- H. Blockeel, L. Dehaspe, B. Demoen, G. Janssens, J. Ramon, and H.Vandecasteele, “Improving the Efficiency of Inductive Logic Programming through the Use of Query Packs,” J. Artificial Intelligence Research, vol. 16, pp.135-166, 2002.
- Ramkumar.S,Elakkiya.A,Emayavaramban.G,” Data Transfer Model - Tracking and Identification of Data Files Using Clustering Algorithms”, IJLTEMAS, Volume III, pp.13-21, Aug2014.
- G. Kollios, M. Potamias, and E. Terzi, “Clustering large probabilistic graphs,” IEEE Trans. Knowl. Data Eng., vol. 25, no. 2, pp. 325 336, Feb. 2013.
- Z. Zou, H. Gao, and J. Li, “Discovering frequent subgraphs over uncertain graph databases under probabilistic semantics,”in KDD, 2010, pp.633–642.
- R. Shamir, R. Sharan, and D. Tsur, “Cluster graph modification problems,” Discrete Applied Mathematics, vol. 144, no. 1-2, pp. 173–182, 2004.
- N. Bansal, A. Blum, and S. Chawla, “Correlation clustering,” Machine Learning, vol. 56, no. 1-3, pp. 89–113, 2004.
- U. Brandes, M. Gaertler, and D. Wagner, “Engineering graph clustering: Models and experimental evaluation,” ACM Journal of Experimental Algorithmics, vol. 12, 2007.
- G. Karypis and V. Kumar, “Parallel multilevel k-way partitioning for irregular graphs,” SIAM Review, pp. 278–300, 1999.
- M. Newman, “Modularity and community structure in networks,” National Academy of Sciences, vol. 103, pp. 8577–8582, 2006.
- M. Newman, “Modularity and community structure in networks,” National Academy of Sciences,vol. 103, pp. 8577–8582, 2006.
- Y. Emek, A. Korman, and Y. Shavitt, “Approximating the statistics of various properties in randomly weighted graphs,” in SODA, 2011, pp. 1455–1467.
|