ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
| V.M. Ramaa Priyaa Assistant professor, Dept of E&I, Bharath University, Chennai-600073, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
In this paper, Probabilistic Neural Network with image and data processing techniques was employed to implement an automated brain tumor classification. The conventional method for medical resonance brain images classification and tumors detection is by human inspection. Operator-assisted classification methods are impractical for large amounts of data and are also non-reproducible. Medical Resonance images contain a noise caused by operator performance which can lead to serious inaccuracies classification. The use of artificial intelligent techniques for instant, neural networks, and fuzzy logic shown great potential in this field. Hence, in this paper the Probabilistic Neural Network was applied for the purposes. Decision making was performed in two stages: feature extraction using the principal component analysis and the Probabilistic Neural Network (PNN). The performance of the PNN classifier was evaluated in terms of training performance and classification accuracies. Probabilistic Neural Network gives fast and accurate classification and is a promising tool for classification of the tumors.
Keywords |
| PNN, Neural Network, PCA, MRI, Classification |
INTRODUCTION |
| Automated classification and detection of tumors in different medical images is motivated by the necessity of high accuracy when dealing with a human life. Also, the computer assistance is demanded in medical institutions due to the fact that it could improve the results of humans in such a domain where the false negative cases must be at a very low rate. It has been proven that double reading of medical images could lead to better tumor detection. But the cost implied in double reading is very high, that’s why good software to assist humans in medical institutions is of great interest nowadays. |
| Conventional methods of monitoring and diagnosing the diseases rely on detecting the presence of particular features by a human observer. Due to large number of patients in intensive care units and the need for continuous observation of such conditions, several techniques for automated diagnostic systems have been developed in recent years to attempt to solve this problem. Such techniques work by transforming the mostly qualitative diagnostic criteria into a more objective quantitative feature classification problem [1,2]. |
| In this paper the automated classification of brain magnetic resonance images by using some prior knowledge like pixel intensity and some anatomical features is proposed. Currently there are no methods widely accepted therefore automatic and reliable methods for tumor detection are of great need and interest. The application of PNN in the classification of data for MR images problems are not fully utilized yet. These included the clustering and classification techniques especially for MR images problems with huge scale of data and consuming times and energy if done manually. Thus, fully understanding the recognition, classification or clustering techniques is essential to the developments of Neural Network systems particularly in medicine problems. |
FEATURE EXTRACTION USING PRINCIPAL COMPONENT ANALYSIS (PCA) |
| In this paper, the principal component analysis (PCA) is used as a feature extraction algorithm. The principal component analysis (PCA) is one of the most successful techniques that have been used in image recognition and compression. The purpose of PCA is to reduce the large dimensionality of the data. |
| MR image recognition systems find the identity of a given test image according to their memory. The memory of a MR image recognizer is generally simulated by a training set. In this paper, the training database consists of a set of MR images. Thus, the task of the MR image recognizer is to find the most similar feature vector among the training set to the feature vector of a given test image. |
| In the training phase, feature vectors are extracted for each image in the training set. Let Ω1 be a training image of image 1 which has a pixel resolution of M x N (M rows, N columns). In order to extract PCA features of Ω1, first convert the image into a pixel vector Φ1 by concatenating each of the M rows into a single vector. The length (or, dimensionality) of the vector Φ1 will be M x N. In this paper, the PCA algorithm is used as a dimensionality reduction technique which transforms the vector Φ1 to a vector ω1 which has a dimensionality d where d << M x N. For each training image Ωi, these feature vectors ωi are calculated and stored. |
| In the testing phase, the feature vector ωj of the test image Ωj is computed using PCA. In order to identify the test image Ωj, the similarities between ωj and all of the feature vectors ωi’s in the training set are computed. The similarity between feature vectors is computed using Euclidean distance. The identity of the most similar ωi is the output of the image recognizer. If i = j, it means that the MR image j has correctly identified, otherwise if i ≠ j, it means that the MR image j has misclassified. Schematic diagram of the MR image recognition system that is implemented is shown in Fig. 1. |
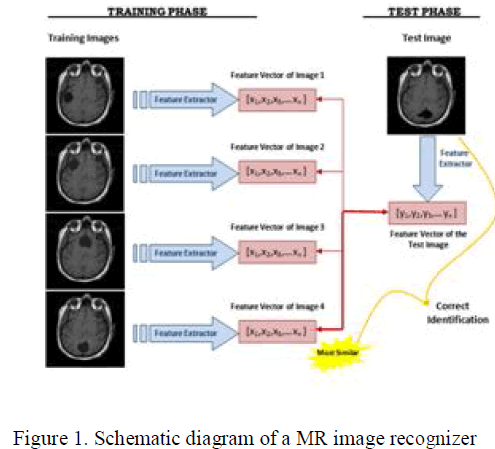 |
PROBABILISTIC NEURAL NETWORK |
| The probabilistic neural network was developed by Donald Specht. This network provides a general solution to pattern classification problems by following an approach developed in statistics, called Bayesian classifiers [3,4]. |
| PNN is adopted for it has many advantages. Its training speed is many times faster than a BP network. PNN can approach a Bayes optimal result under certain easily met conditions [4]. Additionally, it is robust to noise examples. Advance hybrid PNN such as done by Georgiadas et all [5] aimed to improve brain tumor characterization on MRI by using PNN and non-linear MATLAB Neural Network Toolbox. Dimensions of arrays are marked under their names. |
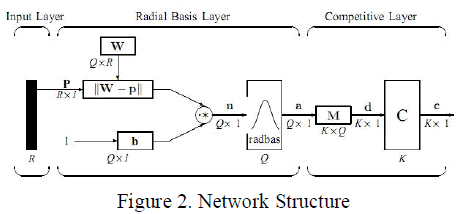 |
| 1) Input Layer: The input vector, denoted as p, is presented as the black vertical bar in Fig. 2. Its dimension is R × 1. In this paper, R = 3. |
| 2) Radial Basis Layer: In Radial Basis Layer, the vector distances between input vector p and the weight vector made of each row of weight matrix W are calculated. Here, the vector distance is defined as the dot product between two vectors [8]. Assume the dimension of W is Q×R. The dot product between p and the i-th row of W produces the i-th element of the distance vector ||W−p||, whose dimension is Q×1, as shown in Fig. 2. The minus symbol, “−”, indicates that it is the distance between vectors. |
| Then, the bias vector b is combined with ||W− p|| by an element-by-element multiplication, represented as “” in Fig. 2. The result is denoted as n = ||W− p|| .p. |
| The transfer function in PNN has built into a distance criterion with respect to a center. In this paper, it is defined as − n 2 transformation of textured features. This method employs a two level hierarchical decision tree discriminate the |
| radbas(n) = e(1) |
| metastatic brain tumor cases from the gliomas and meningiomas (primary brain tumor) cases. At each level, classification was performed using two different LSFT- PNN classifier. LSST-PNN then was compared with the support Vector Machines with Radial Basis Kernel (SVM-RBF) and the Artificial Neural Network (ANN) classifiers. However, we choose a basic Matlab PNN for its simple structure and training manner. |
| The most important advantage of PNN is that training is easy and instantaneous [4]. Weights are not “trained” but assigned. Existing weights will never be alternated but only new vectors are inserted into weight matrices when training. So it can be used in real-time. Since the training and running procedure can be implemented by matrix manipulation, the speed of PNN is very fast. |
| The network classfies input vector into a specific class because that class has the maximum probability to be correct. In this paper, the PNN has three layers: the Input layer, Radial Basis Layer and the Competitive Layer. Radial Basis Layer evaluates vector distances between input vector and row weight vectors in weight matrix. These distances are scaled by Radial Basis Function nonlinearly. Then the Competitive Layer finds the shortest distance among them, and thus finds the training pattern closest to the input pattern based on their distance. The network structure is illustrated in Fig. 2. The symbols and notations are adopted as used in the book Neural Network Design [6]. These symbols and notations are also used by |
| Each element of n is substituted into Eq. 1 and produces corresponding element of a, the output vector of Radial Basis Layer. The i-th element of a can be represented as |
| where Wi is the vector made of the i-th row of W and bi is the i-th element of bias vector b. |
| 3) Some characteristics of Radial Basis Layer: The i-th element of a equals to 1 if the input p is identical to the i- th row of input weight matrix W. A radial basis neuron with a weight vector close to the input vector p produces a value near 1 and then its output weights in the competitive layer will pass their values to the competitive function. It is also possible that several elements of a are close to 1 since the input pattern is close to several training patterns. |
| 4) Competitive Layer: There is no bias in Competitive Layer. In Competitive Layer, the vector a is firstly multiplied with layer weight matrix M, producing an output vector d. The competitive function, denoted as C in Fig. 2, produces a 1 corresponding to the largest element of d, and 0’s elsewhere. The output vector of competitive function is denoted as c. The index of 1 in c is the number of tumor that the system can classify. The dimension of output vector, K, is 5 in this paper. |
METHODOLOGY |
| A description of the derivation of the PNN classifier was given in Chettri and Cromp [7]. PNNs had been used for classification problems. The PNN classifier presented good accuracy, very small training time, robustness to weight changes, and negligible retraining time. |
| There are 6 stages involved in the proposed model which are starting from the data input to output. The first stage is should be the image processing system. Basically in image processing system, image acquisition and image enhancement are the steps that have to do. In this paper, these two steps are skipped and all the images are collected from available resource. The proposed model requires converting the image into a format capable of being manipulated by the computer. The MR images are converted into matrices form by using MATLAB. Then, the PNN is used to classify the MR images. Lastly, performance based on the result will be analyzed at the end of the development phase. The proposed brain MR images classification method is shown in Fig. 3. |
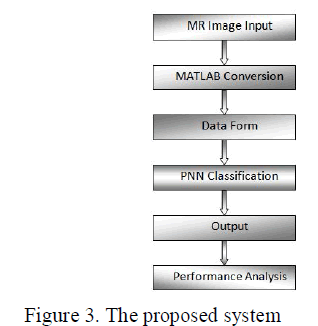 |
RESULTS AND DISCUSSION |
| Various experiments were performed and the sizes of the training and testing sets were determined by taking into consideration the classification accuracies. The data set was divided into two separate data sets – the training data set (20 subjects) and the testing data set (15 subjects). The training data set was used to train the network, whereas the testing data set was used to verify the accuracy and the effectiveness of the trained network for the classification of brain tumors. |
 |
| The PNN was implemented by using MATLAB software package. The spread value (S.V.) of the radial basis function was used as a smoothing factor and classifier accuracy was examined when different values of S.V. were used. If S.V. is near zero, the network will act as a nearest neighbor classifier, and the network will take into account several nearby design vectors if its value becomes larger. |
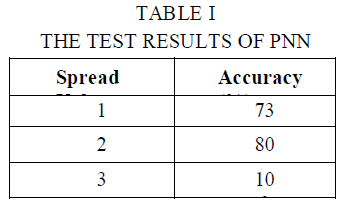
| The developed PNN were examined using 15 testing data. Results are shown in Table I. As shown in Table I, classification accuracy of the testing data set for three spread values 1, 2, and 3 of brain images ranged from 100% to 73%. According to Table I, the classifier presented an accuracy of around 73% when S.V. was 1 and it improved to 80% when S.V. was 2. Classifier performance reached to 100% when S.V. was 3. |
 |
CONCLUSION |
| In this paper, PNN has been implemented for classification of MR brain image. PNN is adopted for it has fast speed on training and simple structure. Twenty images of MR brain were used to train the PNN classifier and tests were run on different set of images to examine classifier accuracy. The developed classifier was examined under different spread values as a smoothing factor. Experimental result indicates that PNN classifier is workable with an accuracy ranged from 100% to 73% according to the spread value. |
ACKNOWLEDGMENT |
| The authors wish to thank MOSTI under Vot 79316 and Universiti Teknologi Malaysia (UTM), 81310 Skudai, Malaysia for supports |
References |
|