ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
B.Nagalakshmi1, .D. Venkatesh2 , K Ramesh3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Broadcasting in an adhoc wireless network where all nodes of the network are sources that want to transmit information to all other nodes. Local Broadcast Algorithms in Wireless Ad Hoc Networks have reduced the transmissions but not concentrated on security security and energy efficiency. Privacy threat and energy efficiency are the major factors in multihop wireless media, Attacks such as traffic analysis and flow tracing can be easily launched by a malicious adversary due to the open wireless medium.These can be achieved with Network Coding Technique and Probability Scheme. Network coding encounters the attacks and reduce the transmissions by applying the coding/mixing operation is encouraged at intermediate nodes. Our goal is to achieve energy efficiency, it directly affects battery life and thus network lifetime. We discussed that applying ideas from network coding allows to realize significant benefits in terms of energy efficiency for the problem of broadcasting, and proposed very simple algorithms that allow realizing these benefits in practice. In particular, our hypothetical analysis shows that network coding improves performance. We show with the experimental simulations that our proposed system will be having the double advantages of reducing the number of transmissions with the enhanced security with great energy efficiency.
Keywords |
| MANET, Network Coding ,Broadcasting, Connected DominatingsSet |
INTRODUCTION |
| Wireless ad hoc networks supports applications,where it is required to have wireless communications among= a variety of devices without depending on any infrastructure. In ad hoc networks, wireless devices are simply called= nodes and also have limited transmission range. Therefore, each node may directly communicate with only those= within its limited transmission range. A node requires other nodes to act as routers in order to communicate with outof= range destinations to broadcast packets. Broadcasting is one of the basic operations in wireless ad hoc networks,= where a node circulates a message to all other nodes in the network. Broadcasting in ad hoc networks cause more= challenges than the one in wired networks for two reasons: node mobility and insufficient system resources [1]. Because of the diversity in node movement patterns, there is no= single optimal scheme for all situations in ad hoc networks. Tree-based schemes such as minimal connected= dominating set (MCDS) [2] are better in reducing resource consumption in a low mobility environment. A set of= nodes form a Dominating Set (DS) if every node in the network is either in the set. A DS is called a Connected= Dominating Set (CDS) if the sub graph induced by its nodes is connected. On the other hand, any CDS can be used= for broadcasting a message only nodes in the set are required to forward. Therefore, the problems of finding the= smallest number of required transmissions and finding a Minimum Connected Dominating Set (MCDS) can= be reduced to each other. Unfortunately, finding a MCDS was proven to be NP hard even when the whole network= topology is known [3], [4]. Williams and Camp [2] divided broadcast methods into four types: simple flooding,= probability based methods, neighbor knowledge based methods and area based methods. When a packet is broadcast= via simple flooding, it is forwarded by every node in the network exactly once. Simple flooding makes sure the= coverage, but it also has the largest forward node set and may cause network congestion and collision.= Simple flooding is the only way to reach the full coverage in high mobility location. That is, the broadcast= packet is assured to be received by every node in the network, providing there is no packet loss created by= collision in the MAC layer. This can be achieved through flooding, in which every node sent out the message after= receiving it for the first time. However, flooding can force a large number of redundant transmissions, which can= result in major waste of constrained resources such as power and bandwidth. In wide-ranging, not every node is= required to transmit the message in order to distribute it to all nodes in the network. Probability scheme and areabased= methods [5] are proposed to solve the so-called broadcast storm problem. In these schemes, each node will estimate its potential input to the overall broadcasting before forwarding a relay packet. If the estimated contribution= is lower than a given threshold, it will not send the packet. These methods generate smaller forward node sets than= simple flooding. Neighbor-knowledge-based methods are based on the following scheme: To avoid flooding the entire= network, a small set of forward nodes is preferred. The challenge is to select a small set of forward nodes in the= absence of global network information. It has been proved that finding the smallest set of forward nodes with= global network information is NP-hard. In the absence of global network information, this problem is even more= challenging. |
| Heuristic methods are normally used to balance cost in collecting network information and in decision= making and effectiveness in deriving a small connected dominatingset. Neighbor knowledge-based algorithms can= be further divided into neighbor-designating methods and self- pruning methods. In neighbor-designating methods [5],= the forwarding status of each node is determined by its neighbors. Basically, the source node picks a division= of its 1-hop neighbors move forward nodes to envelop its 2-hop neighbors. This forward node register is piggybacked= in the transmit packet. Each node in turn designates its own forward node list. Most neighbor-designating methods= use similar heuristics. In multipoint relaying, the complete 2-hop neighbor set shall be covered, since it is independent= of any particular broadcasting. In dominant pruning only a limited 2- hop neighbor set shall be covered by taking the= advantage of routing history information; nodes that are also the 1-hop neighbors of the previous visited node are= excluded in the current coverage. An efficient algorithm is proposed, where not only the 1-hop neighbors but also= some of the 2-hop neighbors of the last visited node are excluded from the current set to be covered. In self-pruning,= each node makes its local decision on forwarding status: forwarding or non-forwarding. Although these algorithms= are based on similar ideas, this comparison is not recognized or discussed in depth. Fair comparison of these= algorithms is complicated by the need of in-depth understanding of the effect of the underlying mechanisms, such as= neighborhood information gathering, piggybacking routing history in relay packets, type of priority value to= establish a total order among hosts, etc. Using local information such as k-hop neighborhood= information for a small k, the forward node set is selected during a distributed and local pruning method.= The forward node set can be constructed and maintained through either a proactive process (up-to-date) or a reactive= process (on-the-fly) [6]. In a reactive process, the result at each node can be postponed so that it has higher chance of= becoming a non-forward node by overhearing its neighbors’ forwarding behavior. Different implementations of= probability self- pruning based on k-hop neighborhood information are collected, and their performances are= compared during simulation. |
| The rest of the paper is organized as follows: In Sections 2 and 3, we analyse the power of local broadcast= algorithms based on the position information and dynamic approach, respectively. In Section 4, we use to explain the= probability to bring heuristic way to find the path. In section 6, simulation to confirm the analytical results presented.= Finally, we conclude the paper in Section 7. |
USING POSITION NFORMATION |
| In broadcast algorithm, the situation is based on the static approach that may desire to know whether to= use location information that can help us to yield a small heuristic factor. A constant heuristic factor is not= achievable if position information is available. |
| In wu Algorithm [7], partitions the network area into square cells. To save energy, at every time the algorithm= selects one node in each cell as active and puts other nodes in the cell to sleep. The set of active nodes must form a= CDS in order to preserve network connectivity and coverage. To guarantee this, the proposed algorithm in [7]= assumes that the side length of each square cell is R/√5, where R is the radio transmission range. However, this is= notenough to guarantee connectivity, because some square cells may not include any node. Under some conditions,= the set of nodes constructed by selecting one node in each nonempty set form a CDS. These conditions can be= relaxed at the price of selecting more than one yet a constant number of nodes in some nonempty cells. Therefore,= the result can be used to expand the work where some cells may contain no working sensor due to failure, a non= uniform distribution of sensors and sensor mobility. In [8], authors use a network partitioning approach in designing= broadcast protocols for dense mobile ad hoc networks. To handle mobility, the proposed broadcast protocols in [8]= rely on the distribution of nodes as opposed to the majority of existing broadcast protocols that rely on frequently= changing communication topology. |
BROADCASTING USING THE DYNAMIC APPROACH |
| Using the dynamic approach, the status of each node is determined “on-the-fly” as the broadcasting packet= propagates in the network. In neighbor-designating broadcast algorithms, for each forwarding node selects a sub set= of its neighbors to transmit the packet and in self-pruning algorithms each node determines its own status based on a= self-pruning condition after receiving the primary/several copies of the message. It was in recent times proved that self-pruning broadcast algorithms are able to guarantee both full delivery and a constant approximation factor= to the optimum solution (MCDS) [9]. However, the proposed algorithm in [9] uses position information in order to= plan a strong self-pruning state. In the previous section, we observed that position information can simplify the= problem of reducing the total number of broadcasting nodes. Position information may not be practical in some= applications .If both full delivery and a constant approx-imation factor can be achieved when position information is= not available. Design a probability broadcast algorithm and show that the algorithm can achieve both full delivery= and constant heuristic only using connectivity information. Before broadcasting a packet, find the probability ratio to= transmit the packet at the minimum transmission. Probability can calculate by using bandwidth of a node,= distance between nodes and signal length. Estimating the probability for each node will lead to find the accurate= path with minimum transmission and cost. |
| Algorithm1. The proposed probability algorithm executed by a node x |
| 1: Extract id’s of the broadcasting node and the selected node from the received message m |
| 2: if x have broadcast the message m before then |
| 3: Reject the message |
| 4: end if |
| 5: if x receives message m for the first time then |
| 6: Create and fill the list Listx(m) |
| 7: Check for probability threshold |
| 8: end if |
| 9: Update the list Listx(m) |
| 10: Remove information added to the message by the previous broadcasting node |
| 11: if Listx(m) ≠0; then |
| 12: Select an id from Listx (m) and add it to the message |
| 13: Schedule the message (*only update the selected id if m is already in the queue*) |
| 14: Listx (m) (* Listx(m) =0 in this case*) |
| 15: ifx was selected then |
| 16: Schedule the message |
| 17: Update the value of probability for each node |
| 18: else |
| 19: Remove message from the queue if x has not been selected by any node before |
| 20: end if |
| The proposed algorithm studies the following: |
| 1. X discards a received message m if it has broadcast m before. |
| 2. If x is selected to forward the message, it schedules a broadcast and never removes the messages from the queue= in future. However, x may change or remove the selected node’s id from the scheduled message every time it= receives a new copy of the message and updates Listx (m). |
| 3. Suppose x has not been selected to forward the message by time t and the Listx (m) becomes empty at time t for= every update. Afterward at time t, it removes the message from the MAC layer queue if the message has been= scheduled before and is still in the queue. |
| 4. If Listx (m) ≠0 then x select a node from Listx (m) ≠0 to forward the message and add the id of the selected= node in the message. The selection can be done randomly or based on a criterion. For example, x can select= the node with the minimum id or the one with maximum battery life-time.5. If x has been selected to forward and= Listx (m) =0 it does not select any node to forward the message. This is the only case where a broadcasting node does= not select any of its neighbours to forward the message. |
PROBABILITY BROADCAST ALGORITHM |
| One direction to optimize neighbor-designating is to take a probabilistic approach. In order to broadcast, a node in= the network broadcasts a message with probability p and takes no achievement with probability 1− p. The= possibility of applying a fact well studied in percolation theory and random graphs. A phase transition is a basis for= selecting p. A certain threshold for p, in graphs and lattices of a certain density for percolation, an unlimited spanning= cluster suddenly appears instead of a set of finite clusters. An infinite spanning cluster is an unbounded connected element, which if transposed to a MANET would translate in the very high probability of the existence of a multi-hop= path between any two nodes within the network. |
| Probabilistic broadcast for neighbor-based in MANETs, have not done so within the context of phase transition. To= the contrary of [10], focus on pure neighbor based in order to know the variations in performance due solely to the= parameters simulating realistic MANET environments. Results provide a general understanding of the behavior to be= expected from probabilistic flooding. |
| A phase transition is a phenomenon where a system undergoes a sudden change of state: small changes of a= given parameter in the system induce a great shift in the system’s global performance. This abrupt transition occurs at= a specific value pc called the critical point or critical threshold. Below pc the system is said to be in a subcritical= phase the global performance is non-existent. Above pc the system is in a supercritical phase and the global property= may be almost surely observed. It would be extremely cost-efficient to observe phase transition in a probabilistic= broadcasting algorithm within all or known subsets of topologies [11]. The probability algorithm estimates the= potential value by using the bandwidth, transmission range and distance between the nodes. The proposition within= such cases would be that there exists a certain probability threshold pc <1 at which the relay message will almost= surely reach all nodes within multihop broadcast reach. Broadcasting with a probability p > pc will not provide any= significant improvement. |
NETWORK CODING |
| Network coding is a networking technique in which transmitted data is encoded and decoded to increase= network throughput and accumulate the various transmissions. The conventional transmissions are decoded at their= destinations. This means that less transmissions are required to transmit the data, but this needs more processing at= intermediary and terminal nodes. |
| Network coding refers to a scheme where a node is allowed to generate output data by mixing (i.e.,= computing certain functions of ) it receives the data. The exclusive characteristics of wireless medium render= network coding mostly useful. For example, network coding can be used to achieve the minimum energy-per-bit= for multicasting in a wireless ad-hoc network. In addition to optimizes energy effectiveness, the network coding= based scheme has only polynomial time complexity breaking through the NP-hardness barrier of the= conventional routing approach. As another case, recently network coding has been developed into a link layer= enhancement technique. The network coding engine in the link layer can opportunistically mix the outgoing= packets to reduce the transmissions in the air. |
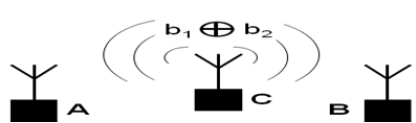
| In today’s practical communication networks such as the Internet and wireless networks, information= delivery is performed by routing, that is it having intermediate routers store and forward t h e data. Network= coding is a recent generalization of routing in which nodes can generate output data by encoding (i.e.,= computing certain functions of ) previously received input data. As illustrated by Figure 1, in network coding,= each node in a network can perform some calculation, whereas in routing the output messages can only be copies= of received messages. Automatically, network coding allows information to be “mixed” at a node. |
| The potential advantages of network coding over routing include resource (e.g., band width) efficiency,= computational efficiency, and robustness to network dynam- ics, network coding is perceived to be useful in= multicast streaming networks, wireless mesh networks, messaging networks, storage networks, , file-sharing peer-topeer= networks and other networks where the same data needs to be transmitted to n number of destination nodes. The= usual topology change that occurs in peer-to-peer networks poses a challenge to the network coding technique because= it complicates network synchronization. In accumulation, the peers may need a large amount of processing time while= trying to decode data. Overall, large networks can increase their efficiency through the use of network coding, but high= operating costs may make them less amenable for small networks. |
NC and wireless communications |
| Transmit b1 from A to B and b2 from B to A using node C as a relay and A and B are not in communication range= (r).Without network coding, 4 transmissions are required to transmit message from A to B.With network coding,= only 3 transmissions are needed |
 |
SIMULATION RESULTS |
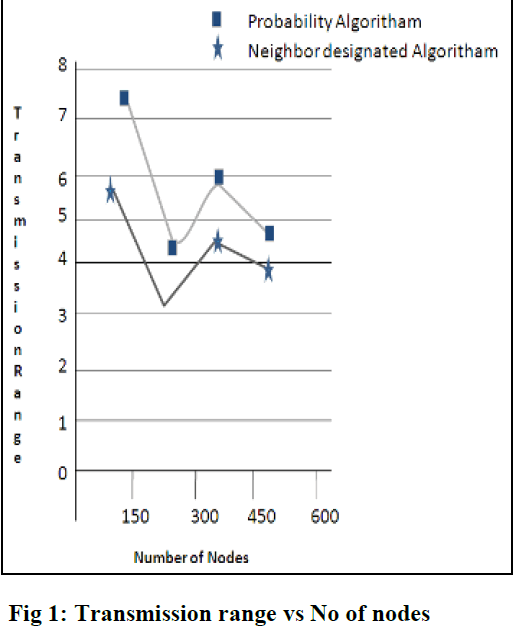
| The design of a probability broadcast algorithm based on the dynamic approach (Algorithm 1) that can= achieve both full delivery and a constant heuristic factor to the optimum solution without using position information.= Figure 1 shows that the range of transmission is high when we using the probability algorithm for more number of= nodes compared to the neighbor designating algorithm. In neighbor designating algorithm there may be a chance for= data loss whereas broadcasting packets. So by using the approach of probability, it may reduce the number of= transmission inorder to avoid the data loss during transmission. |
 |
 |
| Figure 1 set the transmission range to 8 m and varied the total number of nodes from 25 to 500. The= transmission range and the total number of nodes were selected from a large interval so that the simulation= covers very sparse and very dense networks as well as the networks with large diameters. |
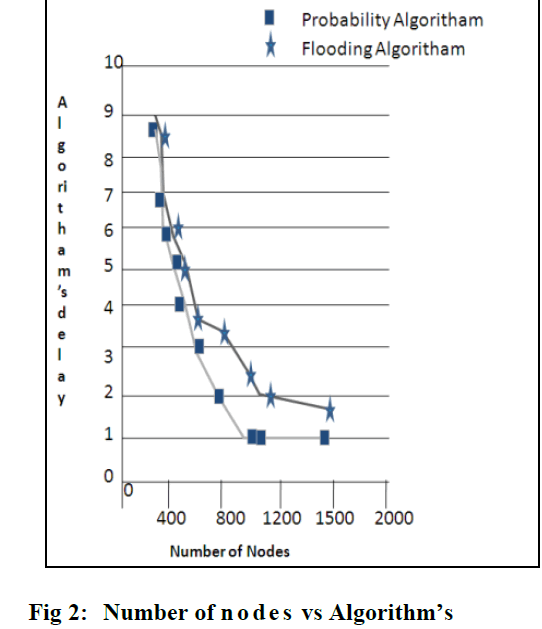
| In Figure 2 shows the efficiency of using probability approach in broadcast algorithm to deliver the packets= from source to destination with low delay compared to other algorithms. |
CONCLUSION |
| In this paper, we explore capabilities of local broadcast algorithms to reducing the total number of transmissions= that are required to achieve full delivery with no data loss. Local broadcast algorithms based on the static approach= cannot guarantee a small sized CDS if the position information is not available. In probability approach, without using the position information, can achieve a constant heuristic factor and full delivery= without packet loss. This approach is more efficient to reducing the transmission inorder to relay the packets to the= destination and enhance the security. These approaches based on the dynamic approach can be extended to the case= where nodes have different transmission ranges or when the network is modeled using the quasi-local unit disk= graph model. |
References |
|