Production of Bricks for Building Construction and Predictability of Its Post-Fired Volume Shrinkage Based on Apparent Porosity and Water Absorption Capacity

Abstract

The high demand for durable building materials has led to the growing rate of production and application of bricks. Successful predictability of Post-Fired Volume Shrinkage (PFVS) was carried out based on its apparent porosity and water absorption capacity (WAC). The bricks were produced from clay which was prepared and processed, following a well detailed step-wise route. Prediction of the PFVS was carried out using a two-factorial empirical model expressed as; ϑ = - 0.3988 ₰ – 0.3789 ξ + 39.256 The validity of the derived model was rooted in the core expression ϑ - 39.256 = - 0.3988 ₰ - 0.3789 ξ where both side of the expression correspondingly approximately equal. Results from both experiment and model prediction shows that decrease in PFVS resulted to increase in apparent porosity and WAC. This implied that the inter-particle spacing increased (with decreasing PFVS) to allow increased water absorption as result of increased apparent porosity. Results from evaluations indicated that the standard error incurred in predicting PFVS for each value of the WAC & apparent porosity considered, as obtained from experiment, derived model and regression model were 0.0842, 0.0010 and 0.0033 & 0.0834, 0.0011 and 4.2286 x 10-5 % respectively. Furthermore the correlation between PFVS and WAC & apparent porosity as obtained from experiment, derived model and regression model were all > 0.97. The maximum deviation of the model-predicted water absorption (from experimental results) was less than 5.57%. This translated into over 94% operational confidence for the derived model as well as over 0.94 effective response coefficients of WAC and apparent porosity to PFVS of the bricks

Keywords

Brick Production, Post-Fired Volume Shrinkage, Apparent Porosity, Water Absorption Capacity.

Introduction

Failures resulting from the deleterious effects of pores on the strength of ceramic materials have raised the need for intensive research and development geared towards production of ceramics with very little porosity; capable of withstanding load. Pores affect the strength of ceramics adversely, not only because they reduce cross-sectional area, over which the load is applied, but more importantly act as stress concentrators. [1] Typically strength and porosity are related in the expression [1];

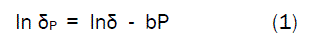
Where δp and δO are strengths of specimen with and without porosity respectively.

It is strongly believed that bricks designated for building constructions should have a least both low porosity and water absorption capacity if it would be un-susceptible to abrupt failure and stand the test of time and environment. These bricks are also expected to have good structural stability through improvements in its chemical, physical and mechanical properties.

Report [2] has shown that fine particles are denser, shrink more, and exhibit excellent mechanical properties. The report also shows a significant evaluation of the relationship between particle size and size distribution with linear drying shrinkage. Results from the evaluation basically indicate that firing shrinkage and apparent porosity have no visible relationship with particle size and linear drying shrinkage. It was therefore concluded based on these results that the finer the particle size, the lesser the apparent porosity and greater the bulk density.

Further researches [1-4] on clay shrinkage during drying have revealed that porosity influences the swelling and shrinkage behaviour of clay products of different geometry. It was reported [3] that drying occurs in three stages; increasing rate, constant and decreasing rate. The researcher pointed out that evaporation rate was higher than evaporating surface during the increasing rate, hence more water is lost. At constant rate, the evaporation rate and evaporation surface are constant. The researcher reported that shrinkage occurs at this stage. Results of similar studies [4] also suggested that at this stage, free water is removed between the particles and the inter-particle separation decreases, resulting in shrinkage. During the decreasing rate, particles make contacts as water is removed, which causes shrinkage to cease.

An empirical analysis of the overall volume shrinkage in molded clay products (from initial air-drying stage to completion of firing at a temperature of 12000C), was carried out using a two-factorial model [5].

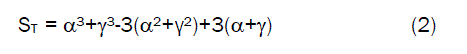
Comparative analysis of results of the overall volume shrinkage predicted by the model and those evaluated from the conventional equations indicated proximate agreement. The overall volume shrinkage was found to depend on direct values of the dried  and fired shrinkage  for its precision. Overall volume shrinkage was found to increase with increase in dried and fired shrinkages until overall volume shrinkage reaches maximum.

Assessment evaluation of the volume shrinkage resulting from the initial air-drying of wet clay was carried out using a univariate model [6]. The model expressed as;

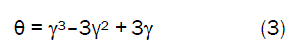
was found to be third-order polynomial in nature. It calculates the volume shrinkage θ when the value of dried shrinkage , experienced during air-drying of wet clays is known. Olokoro clay was found to have the highest shrinkage during the air drying condition, followed by Ukpor clay while Otamiri clay has the lowest shrinkage. Volume shrinkage was discovered to increase with increase in dried shrinkage until maximum volume shrinkage was reached, hence a direct relationship.

The present work aims at producing brick for building construction and also predicting its post-fired volume shrinkage based on apparent porosity and water absorption capacity.

Materials and Methods

The materials used for this research work includes Olokoro Clay mined at Umuahia, Imo and Bentonite obtained from Bridge Head Market, Onitsha, Anambra state, Nigeria. The chemical composition of the clay used is shown in Table 1.

Clay Sizing and Moulding

Size analysis of the clay was carried out using an assembly of sieves having opening as 100, 300 and 1000 μm in ascending order. The sieve assembly was placed on a mechanical sieve shaker and power supply switched on. The set-up was allowed to function for 4 minutes. Particle sizes lesser than 100 μm were taken as fine particle size (A), those at 100 μm were taken as less finer (B), those lesser than 300 μm were taken as medium particle size (C), those at 300 μm were taken as enhanced medium particle size (D) while particle size within range 300-1000 μm were taken as coarse particle size (E). The sieving process was repeated severally until the quantity of clay required for the moulding process was available. Hundred grams (100g) of the sieved clay sample and 10g of bentonite powder were weighed out and thoroughly mixed. To increase the plasticity and strength of the clay material during firing, bentonite powder was added. Six percent (6%) of total weight (clay and Bentonite) of water was added and it was then mixed until complete homogeneity was achieved. The mixed samples were poured into the rectangular metal mould of internal dimension 50 x 18 x 10 mm. The green samples were marked immediately after moulding with two parallel lines (along the length) 70 mm apart. The distance between these lines is L.

Air Drying

The moulded specimens were carefully placed in a plastic tray and kept outside the laboratory to loose some water and become strengthened. The reason for air drying includes (1) to prevent the samples from being defective as a result of evaporation during oven drying and firing (2) to give the specimens adequate strength during oven drying and firing.

Oven Drying and Firing

An electrically heated oven of internal dimension 500 x 500mm was used in the drying operation. The oven was sourced from Erosion Research Center of the Federal University of Technology, Owerri (FUTO). Each set of the specimens was dried at a temperature of 1250C for 1hr, after which their respective weights were measured. The clay samples were then charged into an electric kiln and heated at a lower temperature 1250C, after which the temperature was increased and fired at 12000C for 48 hrs. The samples were cooled in the furnace for 48hrs after firing. The distance between the two parallel lines was determined after oven drying L1 and firing L2.

Determination of post-fired volume shrinkage, apparent porosity and water absorption

Post-fired volume shrinkage V, was calculated using the formular:

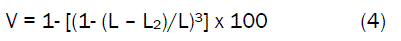
Where

L = Original length (mm)

L1= Dry length (mm)

L2= Fired length (mm)

Apparent porosity and water absorption were determined using the conventional standard technique. [7]

Results And Discussion

The result of chemical analysis of Olokoro clay is shown in Table 1. The table shows that the clay is most constituted by SiO2 and then Al2O3 while Na₂O is the poorest constituent.

Results of the experiment (Table 2) shows that decrease in PFVS resulted to increase in apparent porosity and WAC. This implied that the inter-particle spacing increased (with decreasing PFVS) to allow increased water absorption as result of increased apparent porosity. This is in agreement with past findings [4].

Table 2 shows that as the clay grain size increases, PFVS decreases, resulted to increase in the apparent porosity and invariably water absorption capacity. This is also in accordance with past research [2].

Model Formulation

Experimental data generated from this research work were used for the model formulation. Computational analysis of the data shown in Table 2, gave rise to Table 3 which indicate that;

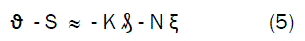
Introducing the values of S, K and N into equation (5) reduces it to;

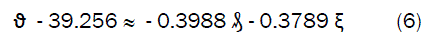
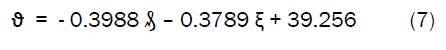
Where

(ϑ) = Post fired volume shrinkage (%)

(₰) = Apparent porosity (%)

(ζ ) = Water absorption capacity (%)

S = 39.256, K = 0.3988, and N = 0.3789. These are empirical constants (determined using C-NIKBRAN [8]

Boundary and Initial Condition

Consider a rectangular shaped clay product of length 49mm, width 17mm, and breadth 9mm exposed to drying in the oven while it was in slight wet condition and then fired in the furnace. Initially, atmospheric levels of oxygen are assumed. Atmospheric pressure was assumed to be acting on the clay samples during the drying process (since the furnace is not air-tight). The sizes of clay particles used were < 100, 100-300 and 300-1000μm while weights of clay and binder (bentonite) used (for each rectangular product) were 100g and 10g respectively. Quantity of water used for mixing was 6% (of total weight). Oven drying and firing temperatures used were 125 and 12000C for 1and 48 hrs respectively. Area of evaporating surface was 833mm2. Cooling time for samples was 48 hrs.

The boundary conditions are: atmospheric levels of oxygen at the top and bottom of the clay samples since they are dried under the atmospheric condition. No external force due to compression or tension was applied to the drying clays. The sides of the particles and the rectangular shaped clay products are taken to be symmetries.

Model Validation

Equation (7) is the derived model. The validity of the model is strongly rooted on equation (6) where both sides of the equation are correspondingly approximately equal. Table 3 also agrees with equation (6) following the values of ϑ - 39.256 and - 0.3988₰ - 0.3789ξ correctly evaluated from the experimental results in Table 2.

Furthermore, the derived model was validated by comparing the model-predicted water absorption and that obtained from the experiment. This was done using the 4th Degree Model Validity Test Techniques (4th DMVTT); statistical graphical, computational and deviational analysis.

Statistical Analysis

Standard Error (STEYX)

The standard errors incurred in predicting PFVS for each value of the WAC & apparent porosity considered as obtained from experiment and derived model were 0.0842 and 0.0010 & 0.0834 and 0.0011 % respectively. The standard error was evaluated using Microsoft Excel version 2003.

Correlation (CORREL)

The correlation coefficient between PFVS and WAC & apparent porosity were evaluated from the results of the derived model and experiment, considering the coefficient of determination R2 from Figs. 2-5. The evaluation was done using Microsoft Excel version 2003.

The evaluated correlations are shown in Tables 4 and 5. These evaluated results indicate that the derived model predictions are significantly reliable and hence valid considering its proximate agreement with results from actual experiment.

Graphical Analysis

Comparative graphical analysis of Figs. 6 and 7 show very close alignment of the curves from the experimental (ExD) and model-predicted (MoD) PFVSs.

Furthermore, the degree of alignment of these curves is indicative of the proximate agreement between both experimental and model-predicted PFVS.

Comparison of derived model with standard model

The validity of the derived model was also verified through application of the regression model (Reg) (Least Square Method using Excel version 2003) in predicting the trend of the experimental results.

Comparative analysis of Figs. 8 and 9 shows very close alignment of curves and areas covered by PFVS, which precisely translated into significantly similar trend of data point’s distribution for experimental (ExD), derived model (MoD) and regression model-predicted (ReG) results of PFVS.

Also, the calculated correlations (from Figs. 8 and 9) between PFVS and WAC & apparent porosity for results obtained from regression model gave 0.9999 & 1.0000 respectively. These values are in proximate agreement with both experimental and derived model-predicted results. The standard errors incurred in predicting PFVS for each value of the WAC & apparent porosity considered as obtained from regression model were 0.0033 and 4.2286 x 10-5 % respectively.

Deviational Analysis

The deviation Dv, of model-predicted PFVS from the corresponding experimental result was given by

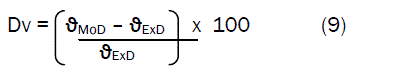
Where

ϑExD and ϑMoD are PFVS obtained from experiment and derived model respectively.

Critical analysis of the PFVS obtained from experiment and derived model shows low deviations on the part of the model-predicted values relative to values obtained from the experiment. This was attributed to the fact that the surface properties of clay and the physico-chemical interactions between the clay and the binder which played vital roles during shrinkage were not considered during the model formulation. This necessitated the introduction of correction factor, to bring the model-predicted PFVS to those of the corresponding experimental values.

Deviational analysis from Table 6 indicates that the precise maximum deviation of model-predicted PFVS from the experimental results is 5.57%. This invariably translated into over 94% operational confidence for the derived model as well as over 0.94 effective response coefficients of WAC and apparent porosity to PFVS of the bricks.

Consideration of equation (9) and critical analysis of Table 6 shows that the least and highest magnitudes of deviation of the model-predicted PFVS (from the corresponding experimental values) are – 4.35 and – 5.57%. Table 6 indicates that these deviations correspond to PFVSs: 23.7398 and 24.2022%, WAC: 17.29 and 16.68%, as well as apparent porosity: 22.48 and 21.90% respectively.

Correction factor, Cf to the model-predicted results is given by

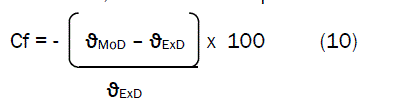
Critical analysis of Figs. 10, 11 and Table 6 indicates that the evaluated correction factors are negative of the deviation as shown in equations (9) and (10).

The correction factor took care of the negligence of operational contributions of the surface properties of the clay and the physico-chemical interactions between the clay and the binder which actually played vital role during shrinkage. The model predicted results deviated from those of the experiment because these contributions were not considered during the model formulation. Introduction of the corresponding values of Cf from equation (10) into the model gives exactly the corresponding experimental values of PFVS.

Figs. 10 and 11 also show that the least and highest correction factor (to the model-predicted PFVS) are + 4.35 and + 5.57 %. Since correction factor is the negative of deviation as shown in equations (9) and (10), Table 6, Figs. 10 and 11 indicate that these highlighted correction factors correspond to PFVSs: 23.7398 and 24.2022%, WAC: 17.29 and 16.68%, as well as apparent porosity: 22.48 and 21.90% respectively.

It is very pertinent to state that the deviation of model predicted results from that of the experiment is just the magnitude of the value. The associated sign preceding the value signifies that the deviation is a deficit (negative sign) or surplus (positive sign).

Conclusion

Brick was produced from clay for application in building construction. Results from both experiment and model prediction shows that decrease in PFVS resulted to increase in apparent porosity and WAC. This implied that the inter-particle spacing increased (with decreasing PFVS) to allow increased water absorption as result of increased apparent porosity. The validity of the derived predictive model was rooted in the core expression ϑ - 39.256 = - 0.3988 ₰ - 0.3789 ξ where both side of the expression correspondingly approximately equal. Results from evaluations indicated that the standard error incurred in predicting PFVS for each value of the WAC & apparent porosity considered, as obtained from experiment, derived model and regression model were 0.0842, 0.0010 and 0.0033 & 0.0834, 0.0011 and 4.2286 x 10-5 % respectively. Furthermore the correlation between PFVS and WAC & apparent porosity as obtained from experiment, derived model and regression model were all > 0.97. The maximum deviation of the model-predicted water absorption (from experimental results) was less than 5.57%. This translated into over 94% operational confidence for the derived model as well as over 0.94 effective response coefficients of WAC and apparent porosity to PFVS of the bricks.

References

1. Barsoum M. 1997, Fundamentals of Ceramics. McGraw Hill Incorporated, Singapore p410
2. Viewey F and Larrly P. 1978. Ceramic Processing Before Firing, John-Wiley and Sons, New York, pp. 3-8.
3. Reed J. 1988, Principles of Ceramic Processing,Wiley Interscience Publication, Canada pp. 470-478.
4. Keey RB. 1978. Introduction to Industrial Drying Operations, Pergamon Press, Elmsford, New York. pp.132-157.
5. Nwoye CI, Iheanacho IO, Onyemaobi OO. Model for the Evaluation of Overall VolumeShrinkage in Molded Clay Products from Initial Air-Drying Stage to Completion of Firing. Int J Nat Appl Sci. 2008;4(2): 234-238.
6. Nwoye CI. Mathematical Model for Computational Analysis of Volume Shrinkage Resulting from Initial Air- Drying of Wet Clay Products. Int Res J Eng Sci Tech. 2008;5(1): 82-85.
7. BS EN ISO 10545-3: 1997
8. Nwoye CI. 2008. C-NIKBRAN ‘‘Data alytical Memory’’- Software.