The proposes a new methodology for solve the Profit Based Unit Commitment (PBUC) problem. The UC problem is solving to Improved Pre-prepared Power Demand (IPPD) table. In a deregulated environment, generation companies (GENCOs) schedule their generators to maximize profits rather than to satisfy power demand The proposed approach has been tested on 3- and 10 units for a scheduling horizon of 24 Comparison of results of the proposed method with the results of previous published methods shows that the proposed approach provides better qualitative solution with less computational time.
Keywords |
| Profit Based Unit Commitment (PBUC), Improved Pre-prepared Power Demand table (IPPD) |
| NOMENCLATURE |
| PF Profit of GENCOs |
| RV Revenue of GENCOs |
| TC Total cost of GENC |
| F(Pij) Fuel cost function of jth generating unit at ith hour |
| Xi j ON/OFF status of jth generating unit at ith hour |
| Pij Output power of jth generating unit at ith hour |
| SPi Spot price at ith hour |
| T Number of hours |
| N Number of generating units |
| PDi Power demand at ith hour |
| Rij Reserve jth generating unit at ith hour |
| SR Spinning reserve at ith hour |
| Pij min Min output power of jth generating unit at ith hour |
| Pij max Max output power of jth generating unit at ith hour |
| ai,bi,ci Coefficients of fuel cost of unit ‘i' |
| Tj
on Minimum time that the jth unit has been continuously online |
| Tj
off Minimum time that the jth unit has been continuously offline |
| Tj
up Minimum up time that the jth unit |
| Tj
down Minimum down time that the jth unit |
INTRODUCTION |
| The Profit Based Unit Commitment (PBUC) problem is one of the most important optimization problems to relating
power system operation under deregulated environment. Earlier, the power generation was dominated by vertically
integrated electric utilities (VIEU) that owned most of the generation, transmission and distribution sub-systems. Recently,the electric power utilities are un-bundling these sub-systems as part of deregulation process. Deregulation requires to
unbundling of vertically integrated power system into generation (GENCOs), transmission (TRANSCOs) and distribution
companies (DISCOMs). The main aim of deregulation is to create competition among generating companies and provide
choice of different generation options at cheaper price to consumers. The main interest of GENCOs in the deregulation is
maximization of their profit whereas in the VIEUs, the objective is to minimize the fuel cost function. This aspect leads to a
change in strategies to solve existing power system problem caused under deregulation. Since the objective of GENCOs to
maximization of their profit, the problem of UC needs to be termed differently as Profit Based Unit Commitment (PBUC).
Generally, the GENCOs place bids depending on the price forecast, load forecast, unit characteristics and unit availability
in different markets. Mathematically, the PBUC problem is a mixed integer and continuous nonlinear optimization
problem, which is complex to solve because of its enormous dimensionality due to a nonlinear objective function and large
number of constraints. The PBUC problem is divided into two sub- problems. The first sub- problem is the determination of
status of the generating units and second sub- problem is the determination of output powers of committed units. |
| The previous efforts for solving PBUC problem were based on conventional methods such as dynamic
programming and Lagrangian relaxation(LR) [3] methods. Due to the curse of dimensionality with increase in number of
generating units, dynamic programming takes large amount of computational time to obtain an optimal solution. The
Lagrangian Relaxation method provides fast solution but suffers from numerical convergence. |
| It is observed from the literature survey that most of the existing algorithms have some limitations to provide
qualitative solution within considerable computational time. Therefore it is necessary to find a simple and efficient method
for solving unit commitment problem independent of dimensionality and selection of solution specific parameters. In this
context a table called improved prepared power demand table (IPPD) is prepared using the available information of system
generation limits and coefficients of fuel cost function(s). |
| The proposed algorithm was implemented in MATLAB (7 Version). The formulation of the PBUC problem is
introduced in Section II. The description of the algorithm for solving the PBUC problem is given in Section III. Simulation
results of the proposed approach for various generating units are presented in Section IV. Conclusions are given in the last
section. |
PROFIT BASED UNIT COMMITMENT PROBLEM FORMULATION |
| The profit-based UC problem under competitive environment is an optimization problem and can be formulated
mathematically by the following equations: |
| a) The Objective function is maximization of profit for generating companies. |
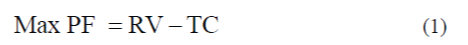 |
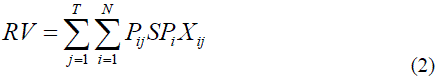 |
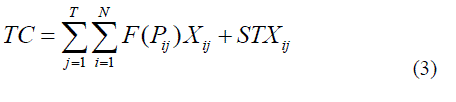 |
Constraints |
| The UC problem is subjected to equality and inequality constraints such as power balance equation, reserve
constraint, limits of units, and the other constraints including the thermal constraints. |
Power balance equation |
| The sum of the output powers of on line generators is equal to the forecasted system power demand in each
period of time. |
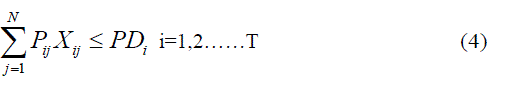 |
| Reserve constraint |
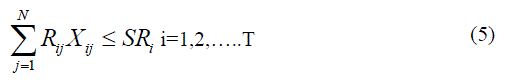 |
Limits of output powers of units |
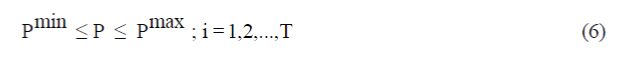 |
Minimum up/down time constraint |
| Minimum up and minimum down time constraints are incorporated in the unit commitment problems as follows. |
 |
 |
SOLUTION METHODOLOGY FOR UC |
Solution of the UC problem is obtained in the following steps: |
| The PBUC problem involves an on and off decision for units depending on variations in power demand. In this
paper, a simple approach has been proposed. |
Formation of the IPPD table: |
| The procedure to form the IPPD table is given below. |
| Step-1 Determine minimum and maximum values of λ for all generating units at their ,min and Pi max. for each
units two λ values are possible. Then arrange these λ va lues in ascending order and index them as λ (where
j = 1,2,....2N ) (9) |
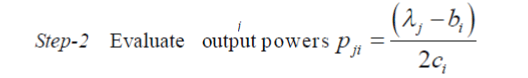 |
| for all generators at each λ j value. Incorporate Pi,min and P i max as below. |
| a. Setting of the minimum output power limit |
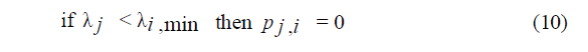 |
 |
| But, for must run generators |
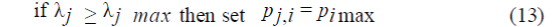 |
| b. Setting of the maximum output power limit |
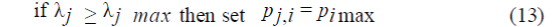 |
| Step-3 λ values, output powers and sum of output powers (SOP) at each λ are arranged in the table in ascending
o r d e r o f λ values. This t a b l e is known as the Improved Preprepared Power Demand (IPPD) table. |
The structure of IPPD table is as follows |
| a. Entries of Column-1 of IPPD table are evaluated λ values arranged in ascending order. |
| b. Entries of Column-2 to Column- N+1 are output powers of each generating unit i subject to constraints
on λ given in eqn. (9)-(12). |
| The last column of IPPD table consists of sum of output powers (SOP) of the generating units at each of the
evaluated λvalue. |
| Here, λ values a r e e v a l u a t e d a t m i n i m um a n d m a x i m um o u t p u t powers. For ‘N’ units
system, 2N lambda values are calculated. Thus the IPPD table has 2N rows and N+2 columns for a system
with N generating units. Assume that the power demand plus spinning reserve lies between SOPj-1 N+2 and SOP j, N+2
Therefore j-1th and jth rows from the IPPD table are selected and form a new table. This table is called Reduced IPPD
(RIPPD) table. |
| The RIPPD table gives the information of the status of the units at selected λ values and also the transition of
commitment of units at one to other λ in the table. The unit commitment schedule for a time horizon having t intervals
will be evaluated from this IPPD table (as explained in procedure below) given the power demand in each time
interval. |
Formation of the Rippd Table: |
| Profit is obtained only when the forecasted price at the given hour is greater than the incremental fuel cost of the
given Therefore, the forecasted price is taken as the main index to select the Reduced IPPD (RIPPD) table from the
IPPD table. |
| There are two options to select the RIPPD table from the IPPD table. |
| Option 1: At the predicted forecasted price, two rows from the IPPD table are selected such that the predicted
forecast price lies within the lambda limits. Assume here that the corresponding rows are m and m+1. |
| Option 2: At the predicted power demand, two rows from the IPPD table are selected such that the predicted
power demand lies within the Sum of Powers (SOP) limits.
Assume here that the corresponding rows are n and n+1. |
| Therefore, the Reduced IPPD table is as follows: |
| ⅰ If m<n, then the RIPPD table is selected based on |
| option 1. Here, the power demand is modified as the SOP of m+1 row. In the PBUC problem, the power
demand constraint is relaxed and it is not necessary to operate the generating units so as to meet power demand. |
| ii If m>n, then the RIPPD table is selected option2.Once the RIPPD table is identified, the information about
the Reduced Committed Units (RCU) table is generated by simply assigning +1 if the output power of the unit
‘i’ pi ≠ 0 and 0 if pi = 0 . The RCU table will have binary elements indicating the status of all units. |
| Now, “incorporation of no-load cost”, “recommitment of units” and “Inclusion of minimum up time and minimum
down time constraints” in the PBUC problem need to be addressed. |
| B. Incorporation Of No Load Cost |
| Formulation of IPPD table is based on incremental fuel cost (λ). Therefore no-load cost is not considered in IPPD
table. In the fuel cost data, some generating units may have huge no-load cost and less incremental fuel costs. Therefore
incorporation of no-load cost
is needed to reduce the total fuel cost. In this paper, a simple approach is proposed to incorporate the no-load cost. |
| Step1 production cost of the units at average of minimum output power and maximum output power is evaluated for all
units. |
| Step 2 all units are arranged in ascending order of the production cost. |
| Step 3 status of the units is also modified according to the ascending order of the production cost. |
| Step 4 Last on-state unit at each hour is identified. Status of the units is changed as follows:
If any unit on the left side of the last on-state unit is in off state then it is converted as on- state unit. |
De-commitment Of Units |
| The committed units may have excess spinning re- serves due to a greater gap between the selected lambda values
in the RIPPD table. Therefore, de-commitment of units is necessary for getting more economical benefits.following steps
are used to de-commit the units. |
| Step-1 Identify the committed units. |
| Step-2 Last unit in the above order is de-committed and spinning reserve is checked. If reserve constraint is
satisfied after de-commit the unit, that unit is de-committed. |
| Step-3 Step -2 is repeated and possible units are de-committed without violating the reserve constraint.
Inclusion of Minimum up time and minimum down time constraints If the off time of the unit is less than the
minimum down time, then status of that unit will be off. If on time of the unit is less than the up time of the unit, then that
unit will be on. |
TEST CASES AND SIMULATION RESULT |
| The proposed approach has been implemented in MATLAB and executed .The proposed has been tested on 3 to 10
generating unit solve profit based unit commitment problems. |
| Example 1 In this example, a 3generating unit system is considered. The fuel cost data of this 3unit system was obtained
from given TABLE 1. |
| In this example, lambda values are computed for all units at their minimum and maximum output powers and arranged in
ascending order. For all lambda values, the output powers are evaluated and IPPD is formulated. |
CONCLUSION |
| The Improved Pre-prepared Power Demand table has been proposed in this paper to solve Profit Based Unit
Commitment (PBUC). While solving the PBUC problem. While solving the PBUC problem, information regarding
the forecasted price is known. Simulation results for the proposed method have been compared with existing methods
and also with traditional unit commitment. It is observed from the simulation results that the proposed algorithm provides
maximum profit with less computational time compared to existing methods and is thus amenable for the real-time
operation required in a deregulated environment. |
| |
Tables at a glance |
 |
 |
 |
 |
 |
| Table 1 |
Table 2 |
Table 3 |
Table 4 |
Table 5 |
|
| |
Figures at a glance |
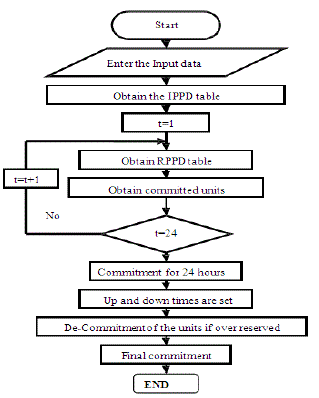 |
| Figure 1 |
|
| |
References |
- Narayana Prasad Padhy, âÃâ¬ÃÅUnit Commitment-A Bib- liographical SurveyâÃâ¬ÃÂ, IEEE Trans on Power Systems, vol. 19, no. 2, May 2004.
- Attaviriyanupap, P., Kita, H., Tanaka, E., and Hasegawa, J., âÃâ¬ÃÅA hybrid LR-EP for solving new profit-based UC problem under competitive environmentâÃâ¬ÃÂ, IEEE Transactions on power systems, vol. 18, no. 1, Feb. 2003, pp: 229: 237.
- Li, T., and Shahidehpour, M., âÃâ¬ÃÅPrice-based unit commitment: A case of lagrangian relaxation versus mixed integer programmingâÃâ¬ÃÂ, IEEE Transaction on Power System, vol. 20, no. 4, November 2005, pp: 2015- 2025.
- Pokharel, B.K., Shrestha, G.B., Lie, T.T., and Fleten, S. E., âÃâ¬ÃÅPrice based unit commitment for Gencos in deregulated marketsâÃâ¬ÃÂ, Proceeding of the IEEE Power Engineering Society General Meeting, 12-16 June, 2005, pp. 2159 -2164.
- Xiaohui, Y., Yanbin, Y., Cheng, W., and Xiaopan, Z., âÃâ¬ÃÅAn improved PSO approach for profit-based unit commitment in electricity marketâÃâ¬ÃÂ, IEEE/PES Trans- mission and Distribution conference & Exhibition: Asia and Pacific, Dalian, China, 2005.
- Richter, Jr., Charles W., and Sheble, Gerald B., âÃâ¬ÃÅA Profit-Based Unit Commitment GA for the Compe-titive EnvironmentâÃâ¬ÃÂ, IEEE Transactions on Power Systems, vol. 15, no. 2, May, 2000, pp. 715- 721.
|