International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Projection's Panel of models for touch screen

Sánchez Juárez Marco Antonio1, Rodolfo Romero Herrera2, Erik Leal Enrriquez3
  1. SEPI-ESCOM, Instituto Politécnico Nacional (IPN), México, D.F
  2. SEPI-ESCOM, Instituto Politécnico Nacional (IPN), México, D.F
  3. Universidad del Valle de México, México, D.F.
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

This article presents a proposal for a three-dimensional holographic projector designed for touch screen device, using optical techniques for your design. We describe the mathematical foundations of it, and why this phenomenon occurs, and provides software that is used to develop the modeling, and the outline of the device, with their respective tests. The result is images that from a touch screen device possible to present them in a glass pyramid. There are commercially projectors of this type; however they do not actually provide a hologram, since the view is the same for either side. The proposal is given a different image for each face.

Keywords
Model 3D, Optics, Modeling, Touch screen, and Pyramid.

INTRODUCTION
Currently the trend toward three-dimensional effects in devices is more common than in previous years. With the arrival of these effects to movies and TV, has become very popular.
But these optical effects are not new, they have had since ancient times, man has sought ways to trick the human eye with different types of effects [1].
Start by defining images as seen by the human eye. This captures the light reflected from the pigment, which are formed objects [2].
This reflex eye captures and interprets it as a color difference of the incident light beam with respect to the pigmentation of which comprises the subject [2] [3] (Figure 1). The human eye is capable of deception, and then to achieve this kind of cheating we will focus based on mathematical foundation optics to achieve the project's development.

RELATED WORK

OPTICS
If we have a beam of light going from point A to point B, and this is reflected on a surface, the trajectory according to Fermat's principle should be the minimum [3]. Taking a medium that does not suffer from disturbances; then the velocity of light is constant in the medium. In order to find the minimal path of the light we have to find the optical path [3], and this can be represented as in figure 2.
As can be seen from Figure 2; a, b, c are constant distances, the angle of incidence i is also constant, and the reflection angle r depend on the result of our analysis, the speed of propagation of the light beam also is constant and does not happen in different ways, but the medium is kept constant and also finding the propagation speed, to find the minimum of the trajectory of the light beam is used basic formulas. Given that time is directly proportional to the distance and inversely proportional to the velocity of the object, in this case our beam. We have that the total time of propagation of the light beam from point A to point B is:
If:
image
Where: t = time
d = distance
v = velocity
Then deduce from (1) to calculate the maximum time in which the light beam passes to Figure 2 is:
image
Where:
(AC)-= the distance from point A to point C
(CB)-= the distance from point C to point B
v = velocity in the middle
From Figure 2 we can define the values of (AC) and (CB) , and substitute into (2) having the following equation:
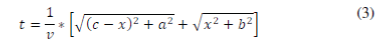image
To find the minimum optical path that need our requirements, we requirement to calculate the time derivative of position with respect to the light beam in the equation (3):
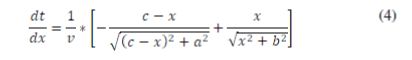image
Fermat's principle we have:
image
Clearing and equating equations (4) and (5) yields the following equation:
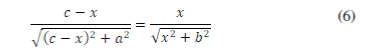image
Using the equivalence breast on the equation (6) we obtain:
image
From equation (7) we can deduce that the incident angle (i) is equal to the angle-reflecting layer (r):
image
After analysis, we can conclude that this is an ideal angle for the projection of images of a device to a suitable surface to develop an optimal design for image recreation space.
According to Fermat's principle [3], we found that by projecting the one surface a light beam, the projection angle or angle of reflection is equal to the angle of incidence.
That is, depending on the angle of the light beam projected on a reflective surface is obtained a reflection angle equal to the incidence, as described in the formula 7. Therefore we can conclude that if that is true for a light beam exemplified by a point or a pixel represented by a light source of a touch screen device could have any projected image on a surface that complies with the law of virtually reflection on a given plane at a certain angle.

MODELING
You need to set the angles you take the pyramid, for which Figure 4 was used. The figure shows the dimensions to calculate any size. See figure 4.
Calculations for building pyramid
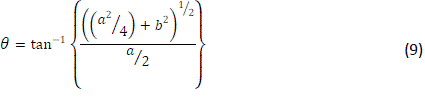image
Rearranging the equation (9) obtain equation (10):
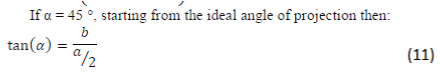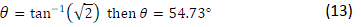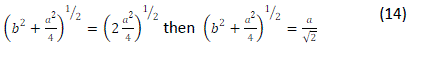image
image
image
image
image
In conclusion each face of the pyramid has a height of a/ √2 and based on
For a better view of the viewer of the projected images is defined as ideal angle π/4 for a view reflected in the same angulations, placing the device in a projection perpendicular with respect to the viewer. Defining this, we can develop a field prototype reflection of the images. See figure 5
Used four sides in order to display four view angles dimensional model also considering a support space at the center of the panel, this in order to place it on the screen of a touch screen device.
Being able to project images through a reflective surface can try to fool the human eye by projecting images with attributes that simulate depth, this in order to use the medium as a canvas projection by reflecting more complex models as are three-dimensional models.
These models may be found in the development of the field of virtual reality, since the object is to appear reality in a virtual environment as shown in Figure 6.
Making use of Aqsis [4] to model this type of scenario and render it by the standards of Pixar RenderMan [5] [6]. Using the basic commands in RenderMan modeling can originate a file type RIB () containing very simple scenarios, in this case, basic models of a sphere. If we separate the different views of the model in four different angles, and project these views on the reflective surface, the characteristics of the object would have placed in another point of view beyond the projection space of a touch screen device.
The properties of depth that we try to emulate our model will also be reflected on the surface, thus causing the effect of the reflecting layer object also contains properties such projection in the middle.
It was proposed to use a touch screen for ease of use when interacting with the figures, since the effect occurs in real time. If you want to rotate an image, the movement can be seen immediately in the glass pyramid.

EXPERIMENTAL RESULTS
It is tested first angle variation for the purpose of determining the angle of refraction suitable, as shown in Table 1. We conclude that this is 1.4.
Through mathematical calculations obtained and basic modeling, it was possible to obtain a projection on different aspects of various basic models within the RenderMan.
As shown in Figures 6 and 7 got the expected result. A cone showed in figure 7 and in figure 8 a sphere. It is important to note how the image is distorted within the pyramid, especially when generating images for the touch screen display, because as the field is observed to deform when present in the pyramid.
The touch screen display provides greater interactivity in real time. If we move our fingers over the screen cause a change in the hologram produced. To achieve the necessary four views generated images on the screen are related to that seen in the views on the faces are moved appropriately, so that always four different views are observed without mismatches. The sample mean if one side in front of a figure, the opposite side of the reverse pyramid should show the back of the figure and same occurs with the side images. Figure 9 shows a cube with four faces of different color, which allows verifying the synchronization of the movements. No problem achieving the holographic effect. So by surrounding the user will notice the different faces with different color.
A more complicated image is an avatar as shown in Figure 9. In this picture is easier to see if there is an error, not only in the timing of movements, we can also see the images corresponding with the expected.
Finally we present a planetary system in the Figure 11; here the animation of the four images is the challenge to overcome. Only if you look carefully you can see which the image is generated on the touch screen and which is the image captured by the raw crystals.

CONCLUSION
It was achieved by generating a hologram of four views by projecting a touch screen, which enhances the interactivity with the user, all in real time. It is important to consider the problems that can arise if not taken into account the angle of reflection, as this may cause distortion of the image, and in the case of spherical objects and animated the result is negative.
The method can be adapted to virtually any screen regardless of the size, because if you have a more grade pyramid need a bigger screen. It can be attached to a cellular and it is possible to get a three-dimensional holographic projection with four views.
By using three-dimensional images achieves a greater sense of realism. However, it must link or relate the images of the four views. Such as, movement on one side to produce a coherent movement in the other three faces.
As future work intends to make the real image capture and perform the corresponding reproduction the glass pyramid.

ACKNOWLEDGMNET
The authors thank the Instituto Politécnico Nacional, a research Section of Graduate Studies and Research of the Escuela Superior de Computo ESCOM for their support.
 

Tables at a glance
Table icon
Table 1
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
Figure 5 Figure 6 Figure 7 Figure 8
Figure 5 Figure 6 Figure 7 Figure 8
Figure 9 Figure 10 Figure 11
Figure 9 Figure 10 Figure 11
 

References