Pseudo-Anonymization of Social Networks
by Sequential Clustering and Classification

S. Tulasi Krishna; M. Vijaya Bharathi

Pseudo-Anonymization of Social Networks by Sequential Clustering and Classification

S. Tulasi Krishna, M. Vijaya Bharathi
Dept of CSE, GMR Institute of Technology, Andhra Pradesh, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

In these days every one placing the personal data like photos, bio data etc. in so many social sites like face book, Gmail, matrimony etc. but the data is not safe in all conditions this problem is called privacy preserving problem. It provides an anonymized view of the data through a unified network, without revealing information to any of the users. Finally we develop an algorithms which is based on sequential clustering that provides centralized settings. This algorithm works based on the SaNGreeA algorithm, because Campan and Truta which is the leading algorithm for achieving anonymity in networks by means of clustering. The disadvantage of SaNGreeA, it builds clusters gradually. It cannot use actual Information Loss. This information loss will be evaluated only when all of the clusters are defined. So it contains structural information loss. But in Sequential clustering algorithm overcome this problem. In this algorithm makes decisions based on the measure of real information loss. Finally it gives a framework to classify the data with less information loss.

KEYWORDS

clustering, data mining, distributed computation, Information Loss, privacy preserving, Social networks.

I. INTRODUCTION

Social networks are have been studied for last so many years in different streams like Biology, Economics, and Sociology etc. In recent days every one uploading the data in social networks such as MySpace, Facebook, Twitter. Even in the few online networks that are completely open so that the data will be shown in online. Most operators provide some privacy to their data. That data is like telephone numbers, emails, messages etc. Generally individual data sets can be stored in simpler, traditional and complex forms. The researchers doing work on these data models and providing different solution to improve the privacy of the data. Although most of the privacy work done in Healthcare data. In this paper manly concentrating on university data that contains student details, employees salary workers details etc. Online social interaction has most popular around the world and this technology drastically increases day by day, most of the researchers also accepted it. For example Facebook, in this site every one personal details, contact numbers, email ids, and photos are also available. So privacy in social sites is infancy. For reason number of techniques are proposed. Generally networks are modeled by a graph, where nodes of the graph are called entities and nodes connecting lines are called edges. These edges represents the relationship between them. Example it is a real social network. A financial network contains more nodes then it becomes more complex. These type of networks are called Asymmetric. Social networks are very curious to do research work because it contains number of departments like sociology, psychology, market research or studies related and epidemiology. However, this social data is published in online. This data contains some sensitive information. Therefore, it is needed to hide that information this is simply called Anonymization. This anonymization can be done in different areas like images, data, graph etc. but here data is anonymized. So the publishing data is anonymized and provided the security to that data in order to achieve the privacy preservation.

II. CONCOMITANT STUDY

Data anonymization characteristically trades off with effectiveness. Therefore, it is required to find a golden path in which the released anonymized data still holds enough utility and privacy preservation to some accepted degree on the other hand. In this paper we propose an anonymization technique based on clustering, the data is formed into clustering the nodes based on loss dynamically forms the clusters nodes likewise it forms big nodes known as super nodes in which each of size at least k, where k is called anonymity parameter means it has to form minimum k nodes. Before this the data is centralized manner so if number of transactions are more then the information loss measure is increase. In order to reduce this problem the data is distributed between the nodes then it is called distributed network. The network data is split between several players.

III. MODELLING

A. GRPAH REPRESENTATION

The social network data is represented in graph formats. Those graphs are directed and undirected graph. Social network is a simple undirected graph. A=(Vi, Ei), A is a graph, Vi is the vertices of the graph and Ei is the edges of the graph where i=0…n.

In the above figure is Facebook graph. That doesn’t representing any directions so it is undirected graph. The images are in circle shape is called vertices vi and connecting between vertices is called edges Ei. for unique identification add some structural information to the edges. Each node is corresponding to an individual in that group it belongs to. Edge connects two nodes and describes a relationship between the two corresponding individuals. Each node has non identifying attributes, such as age, gender, zip code etc. the combination these attributes are called quasi attributes. These quasi identifiers are used for unique identification.

IV. ANONYMIZATION BY CLUSTERING

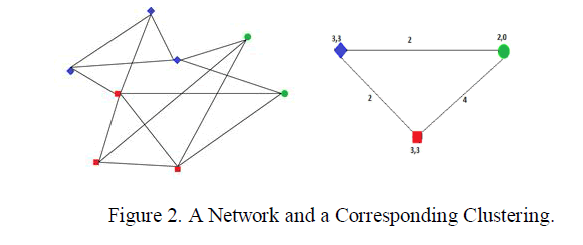Definition 1:

The social network as a simple undirected graph G = (V, E), where V ={V1… VN} is the set of nodes and E ⊆ V1 is the set of edges. Each node corresponds to an individual in the underlying group, while an edge that connects two nodes describea relationship between the two corresponding individuals. Where V1 is the set of unordered pairs of elements from V. In every graph each node can be described by using the non identifying attributes. Those attributes are like zip code, age, sex, roll or employee numbers etc. These attributes are called quasi identifiers or unique identifiers. The combination of identifiers are uniquely identifies the nodes.

An example of a network of eight nodes, with two-dimensional quasi-identifier records and a corresponding clustered network with three super nodes. In the above figure having three colors in different shapes. Let us consider blue color nodes represent age, red color nodes represents location and blue color nodes gender then finally form clusters and finally calculates the information loss between the edges.

Edge Connectivity:

It is the minimum number of edges whose removal results in a disconnected graph. It is denoted by k(G). For a graph G, if k(G) = l then G is called an l-connected graph.

Example:

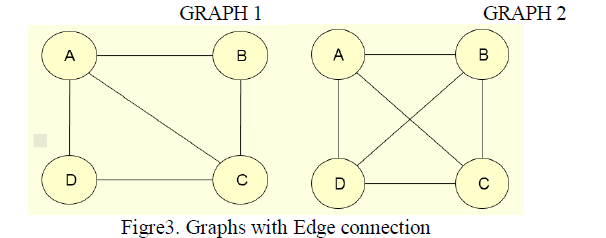The edge connectivity for the GRAPH 1 is 2.

The edge connectivity for the GRAPH 2 is 3.

A cut in a graph is a set of edges whose removal disconnects the graph. A minimum cut is a cut with a minimum number of edges. It is denoted by S. For a non-trivial graph G iff |S| = k(G). The distance d(u,v) between vertices u and v in G is the minimum length of a path joining u and v. The length of a path is the number of edges in it.

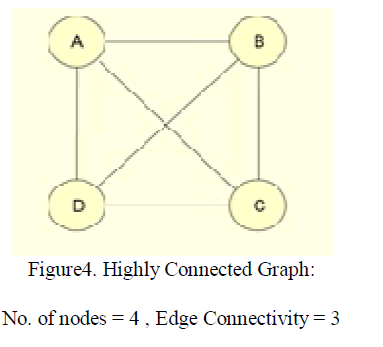
Highly connected graph:

A graph G is k-connected if the removal of any collection of fewer than k vertices from G results in a connected graph with at least two vertices. Highly connected graphs represent robust networks that are resistant to multiple node failures. When a graph is not highly connected, it is useful to partition the vertices of the graph so that every part induces a highly connected subgraph. For example, designed a clustering algorithm where the vertices of a graph G are partitioned into highly connected induced subgraphs. For a graph with vertices n > 1 to be highly connected if its edge-connectivity k(G) > n/2.A highly connected subgraph (HCS) is an induced sub graph H in G such that H is highly connected. HCS algorithm identifies highly connected subgraphs as clusters. Properties: Diameter of every highly connected graph is at most two. That is any two vertices are either adjacent or share one or more common neighbors. This is a strong indication of homogeneity. Each cluster is at least half as dense as a clique which is another strong indication of homogeneity. Any non-trivial set split by the algorithm has diameter at least three. This is a strong indication of the separation property of the solution provided by the HCS algorithm.

The sequential clustering algorithm for k-anonymizing tables was presented in above. It was shown there to be a very efficient algorithm in terms of runtime as well as in terms of the utility of the output anonymization. We proceed to describe an adaptation of it for anonymizing social networks.

A. Anonymization

We categorize anonymization methods on graph formatted data into three main categories:

– Graph modification approaches: These methods anonymize a graph by modifying (adding and/or deleting) edges or nodes in a graph. There are two basic approaches:

ÃÂ¯ÃâÃÂ· The simplest way alters the graph structure by removing and adding edges randomly. It is called randomization or random-based approach.

ÃÂ¯ÃâÃÂ· Another way consists on edge addition and deletion to fulfil desired constraints, i.e. anonymization methods do not modify edges at random, they modify edges to meet some desired constraints. For example, k-anonymity-based approaches modify graph structure (by adding and removing edges) in order to get the k-anonymity value for the graph.

– Generalization approaches (also known as clustering-based approaches): These methods cluster nodes and edges into groups. Then, they anonymize each group into a super-node to publish the aggregate information about structural properties of the nodes. The details about individuals can be hidden properly, but the graph may be shrunk considerably after anonymization, which may not be desirable for analyzing local structures.

– Differentially private approaches: These methods refer to algorithms which guarantee that individuals are protected under the definition of differential privacy [11]. Differential privacy imposes a guarantee on the data release mechanism rather than on the data itself. The goal is to provide statistical information about the data while preserving the privacy of users.

The algorithm then starts its main loop (Steps 2-4). In that loop, the algorithm goes over the N nodes in a cyclic manner and for each node it checks whether that node may be moved from its current cluster to another one while decreasing the information loss of the induced anonymization. If such an improvement is possible, the node is transferred to the cluster where it currently fits best.

In the above algorithm the size of the cluster varies from [2, k1] where k1=βk and β is the fixed parameter. Based upon the main loop the cluster is formed, the data is removed and transferred to other based on best fit. On the other hand information loss (step sd). Likewise this process is continuous until the cluster becomes large means cluster size k. Then it partition the cluster randomly. This process is continuous until all the data should be moved to other clusters and the information loss is minimized. The stopping condition is repeatedly changed based on information loss. In this way we can minimize the information loss.

As a result number of clusters are formed but not all clusters having equal length, some of them having large size and some clusters are not having minimal size means atleast k. so have to apply agglomerative procedure to group all the small clusters into a single cluster. In this process also having some information loss we have to observe that loss also.

Information Loss: In [6], the proposed SaNGreeA algorithm uses a measure of structural information loss that differs from the measure IS (.) that is given by (4)-(6). We proceed to define it. Let B be the N×N adjacency matrix of the graph G=(V,E) i.e B(n,n1) = 1 if {Vn ,Vn1} ∈ and B(n,n1) = 0 otherwise then the hamming like distance is defined on V as follows

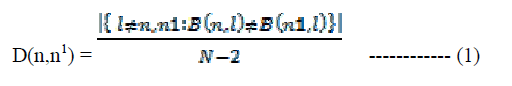This definition of distance induces the following measure of structural information loss per cluster. Based upon the distance metric we can find the loss by using the equation

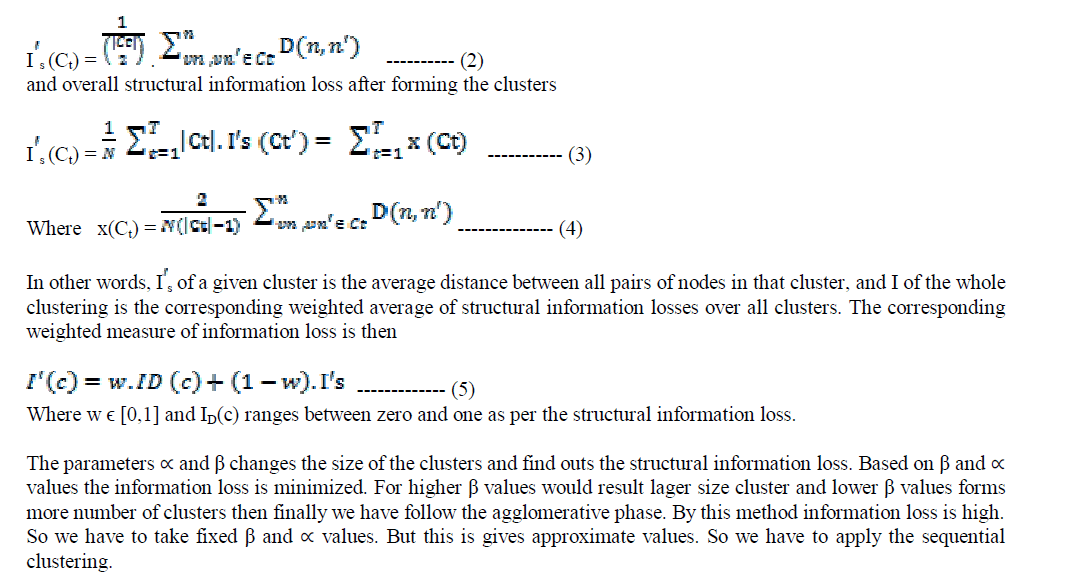V. DISTRIBUTED SEQUENTIAL CLUSTERING

VI. SECURITY

A secure network doesnot share any data to the other parties but it is not good always. Because some basic information is needed for all conditions and visibility of complete information is also not useful. By using distributed sequential clustering the sensitive information is hided in the entire network and all sites are linked to each other so that information loss is also minimized as well basic information will be published in web. Computing the sum of private integers has well known simple SMPs. The components of the vectors are rational numbers The denominators of those numbers are common and known to all, but their numerators depend on private integers, those are the private integers that appear in the numerator Hence, that problem reduces to computing sums of private vectors over the integers. Moreover, it is possible to compute upfront an upper bound p on the size of those integers and of their sum.

VII. NETWORK DATA CLASSIFICATION

Network data is quite popular in Web and social networks applications in which a variety of different scenarios for node classification arise. In most of these scenarios, the class labels are associated with nodes in the underlying network. In many cases, the labels are known only for a subset of the nodes. It is desired to use the known subset of labels in order to make predictions about nodes for which the labels are unknown. This problem is also referred to as collective classification. In this problem, the key assumption is that of homophily. This implies that edges imply similarity relationships between nodes. It is assumed that the labels vary smoothly over neighboring nodes. A variety of methods such as Bayes methods and spectral methods have been generalized to the problem of collective classification. In cases where content information is available at the nodes, the effectiveness of classification can be improved even further. A different form of graph classification is one in which many small graphs exist, and labels are associated with individual graphs.

VIII. IMPLEMENTATION RESULTS

In this paper we taken educational data set which is created in sql language. A university contains all students, faculty and other workers information. Means the data set contains some sensitive information so that the data is represented in graph after that the data is clustered. The result is shown in figure5.

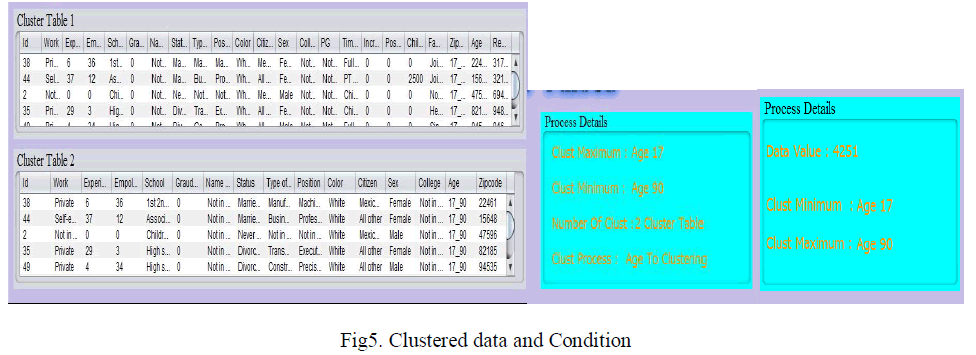Then we apply the anonymization condition on sensitive attributes of the data. so that we can hide the sensitive information. Here the data is clustered based upon the age and zipcode is anonymized and the result is shown in figure6.

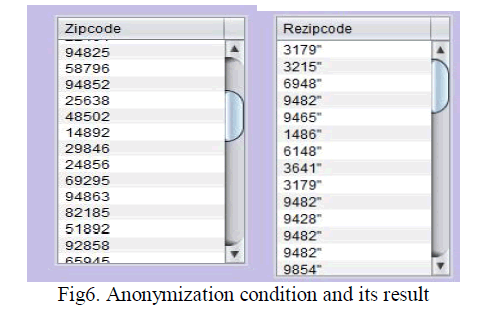And finally calculates the information loss and these results are compared to SaNGreeA algorithm. The graphs are generated based on the loss of information and that graph explains how much effectively performs than compared to previous algorithms.

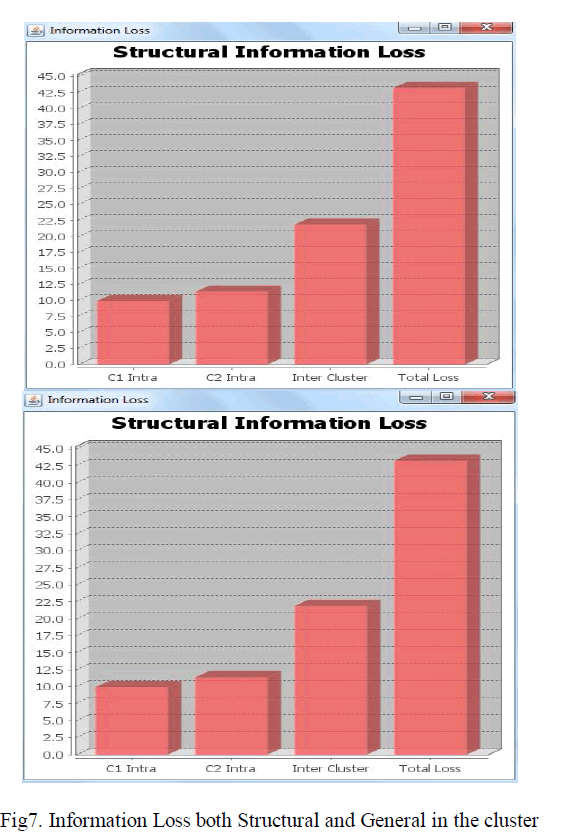IX.CONCLUSION

In this paper we represented university data that contains educational and other sensitive information. That information is distributed among the different sites so it has to be anonymized by one admin and here we used sequential clustering algorithms. The entire data is forms K clusters only so it is not safe all conditions it causes L-diversity problems. And finally I applied classification algorithm in reduce the number of computations every time. In classification if new record entered by using classifiers the record is sorted according to the condition. It is research direction so develop the number of algorithms which is having high security and less information loss.

References

Anonymization of Centralized and Distributed Social Networks by Sequential Clustering Tamir Tassa and Dror J. Cohen IEEE TRANSACTIONS ON KNOWLEDGE AND DATA ENGINEERING, VOL. 25, NO. 2, FEBRUARY 2013
De-anonymizing Social Networks Arvind Narayanan and Vitaly Shmatikov The University of Texas at Austin NSF grants IIS-0534198, CNS-0716158, and CNS-0746888.
Data and Structural k-Anonymity in Social Networks Alina Campan and Traian Marius TrutaDepartment of Computer Science, Northern Kentucky University, Highland Heights, KY 41076, U.S.A. {campana1,trutat1}@nku.edu.
Data Classification Algorithms and Applications Edited by Charu C. Aggarwal IBM T. J. Watson Research Center Yorktown Heights, New York, USA.
A. Campan and T.M. Truta, “Data and Structural k-Anonymity in Social Networks,” Proc. Second ACM SIGKDD Int’l Workshop Privacy, Security, and Trust in KDD (PinKDD), pp. 33-54, 2008.