International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

PSO Technique for Solving the Economic Dispatch Problem Considering the Generator Constraints

Dr. L.V.Narasimha Rao
 Professor, Dept. of EEE, K L University, Guntur, Andhra Pradesh, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

By economic dispatch means, to find the generation of the different units in a plant so that the total fuel cost is minimum and at same time the total demand and losses at any instant must be met by the total generation. The classical optimizations of continuous functions have been considered. Various factors like optimal dispatch, total cost, incremental cost of delivered power, total system losses, loss coefficients and absolute value of the real power mismatch are evaluated for a simple system by hand calculation. The MATLAB programs were developed to solve Economic Load Dispatch Problem of an n-unit Plant through lambda iterative method and Particle Swarm Optimization

Keywords
frequency hopping sequence (FHS) , optimal power flow (OPF)

INTRODUCTION
In a practical power system, the power plants are not located at the same distance from the centre of loads and their fuel costs are different. Also under normal operating conditions, the generating capacity is more than the total load demand and losses. Thus there are many options for scheduling the generation. With large interconnection of electrical networks, the energy crisis in the world and continuous rise in prices, it is very essential to reduce the running charges of electrical energy .i.e. reduce the fuel consumption for meeting a particular demand. In an interconnected power system, the objective is to find the real and reactive power scheduling of each power plant in such a way as to minimize the operating cost. This means that the generators real and reactive powers are allowed to vary within certain limits so as to meet a particular load demand with minimum fuel cost. This is called the optimal power flow (OPF) problem. The OPF is used to optimize the power flow solution of large scale power system. This is done by minimizing selected objective functions. While maintaining an acceptable system performance in terms of generator capability limits and output of the compensating devices. The objective functions, also known as cost functions may present economic costs, system security or other objectives. Efficient reactive power planning enhances operation as well as system security.
In this project our aim was to find optimal solution to the Economic dispatch including losses and generating limits .There are several methods to solve Economic load dispatch problem. Hence we considered one of the conventional methods i.e. lambda iterative method and one of the Artificial Intelligence methods i.e. Particle Swarm Optimization. Lambda iterative method was done by considering a specific lambda value and co-ordination equations were derived. From this equation we got a solution in which inequality constraints imposed on generation of each plant and equality condition were satisfied. Particle Swarm Optimization is also used to solve the same problem. In this method various steps involved are Initialization, Evaluation etc. Through all the above process the optimal solution was derived.The results of both the Lambda iterative method and Particle Swarm Optimization method were compared and the best method was identified as Particle Swarm Optimization method.

ECONOMIC DISPATCH
It considers a network with N mobile unlicensed nodes that move in an environment according to some stochastic mobility models. It also assumes that entire spectrum is divided into number of M non-overlapping orthogonal channels having different bandwidth. The access to each licensed channel is regulated by fixed duration time slots. Slot timing is assumed to be broadcast by the primary system. Before transmitting its message, each transmitter node, which is a node with the message, first selects a path node and a frequency channel to copy the message. After the path and channel selection, the transmitter node negotiates and handshakes with its path node and declares the selected channel frequency to the path. The communication needed for this coordination is assumed to be accomplished by a fixed length frequency hopping sequence (FHS) that is composed of K distinct licensed channels. In each time slot, each node consecutively hops on FHS within a given order to transmit and receive a coordination packet. The aim of coordination packet that is generated by a node with message is to inform its path about the frequency channel decided for the message copying.Furthermore, the coordination packet is assumed to be small enough to be transmitted within slot duration. Instead of a common control channel, FHS provides a diversity to be able to find a vacant channel that can be used to transmit and receive the coordination packet. If a hop of FHS, i.e., a channel, is used by the primary system, the other hops of FHS can be tried to be used to coordinate. This can allow the nodes to use K channels to coordinate with each other rather than a single control channel. Whenever any two nodes are within their communication radius, they are assumed to meet with each other and they are called as contacted. In order to announce its existence, each node periodically broadcasts a beacon message to its contacts using FHS. Whenever a hop of FHS, i.e., a channel, is vacant, each node is assumed to receive the beacon messages from their contacts that are transiently in its communication radius.

EFFICIENT COMMUNICATION
The use of electricity is absolutely necessary in modern day-to-day life. The quality of electricity is stated in terms of constant voltage, constant frequency and uninterrupted power supply at minimum cost. To provide uninterrupted power supply and to return profit on the capital investment we need to cut down the cost of generation of electricity. That means proper operation is very important. There are many factors involved in the successful operation of a power system. The system is expected to supply power instantaneously and continuously to meet customer‟s demands under all operating conditions. It is also expected that the voltage supplied to the consumers need to be maintained at or near the nominal rated value. For this proper operating procedure must be observed to avoid damage to equipment or other facilities of the system. All of these operating requirements must be achieved simultaneously with minimum cost for production and distribution of power. Economic factors influenced by actions of operating personnel include the loading of generating equipment, particularly of thermal units, where efficiency of unit and fuel costs are major factors in the cost of power production. Purchase power availability, cost and scheduling of overhaul and/or repairs of equipment all affect operating costs. The cost of generation includes the fixed costs (like salaries and capital cost etc) and Variable costs (like fuel cost, maintenance cost and operation cost etc. An engineer is always concerned with cost of Product and Services. For a power system to return a profit on the capital invested, proper operation is very important.

2.1Development of Economic Load Dispatch Methods
The progress of optimal dispatch goes far back as the early 1920‟s, when engineers were concerned with the problem of economic allocation of generation or the proper division of the load among the generating units available. Prior to 1930, various methods were in use such as: (a) the base load method where the next most efficient unit is loaded to its maximum capability, then the second most efficient unit is loaded, etc., (b). “best point loading,” where units are successively loaded to their lowest heat rate point, beginning with the most efficient unit and working down to the least efficient unit, etc. It was recognized as early as 1930, that the incremental method, later known as the “equal incremental method,” yielded the most economic results. In 1954, co-ordination equation was developed for solving economic dispatch problem. A breakthrough in the mathematical formulation of the economic dispatch problem was achieved by Carpentier in the early 1960‟s who treated the entire work in an exact manner. The solution of Carpentier‟s formulation is a non-linear optimization which has been the subject of much study though the present and its implementation in real time remains a challenge.
Aoki, et al. presented a new Parametric Quadratic Programming method to solve an economic load dispatch problem with dc load flow type network security constraints.
C.E. Lin and G.L. Viviani presented a method to solve the economic power dispatch problem with piecewise quadratic cost functions. The solution approach is hierarchical, which allows for decentralized computations.
Pereira, et al. described a method for the Economic Dispatch with security-constrained dispatch that can take into account the system rescheduling capabilities. The methodology is based on the Bender‟s Decomposition principle which allows the iterative solution of a base-case economic dispatch and separate contingency analysis with generation rescheduling.
Lin, et al. presented a real time economic dispatch method by calculating the penalty factors from a base case data base. The basic strategy of the proposed method assumes that a base case data base of economic dispatch solution is established according to statistical average of system operation data of the daily demand curve.
Zi-Xiong Liang presented a zoom feature applied to the dynamic programming method for solving economic dispatch of a system of thermal generating units including transmission line losses.
Gerald B. Sheble, et al. proposed a genetic-based algorithm to solve an economic dispatch problem. The algorithm utilizes payoff information of perspective solutions to evaluate optimality.
K.P. Wong and Y.W. Wong established a hybrid genetic / simulated-annealing approach for solving the thermal generator scheduling problem. It develops a method for encoding generator schedules in the hybrid approach..
T. Yalcinoz and M.J. Short proposed a Neural Networks approach for solving Economic Dispatch problem with transmission capacity constraints.
Allen J. Wood, Bruce F. Wollenberg presented a several classical optimization techniques for solving economic Load dispatch problem. These are Lambda Iteration Method, Gradient method and Dynamic Programming (DP) method, etc.

2.2 Economic Load Dispatch - Thermal Stations
A power system is a mix of different type of generations, out of which thermal, hydro and nuclear power generations contribute the active share. However, economic operation has conveniently been considered by proper scheduling of thermal or hydrogenation only. As for the safety of nuclear station, these types of stations are required to run at its base loads only and there is a little scope for the schedule of nuclear plants in practice.Economy of operation is most significant in case of thermal stations, as the variable costs are much higher compared to other type of generations. This can be considered by looking at various costs of different stations.
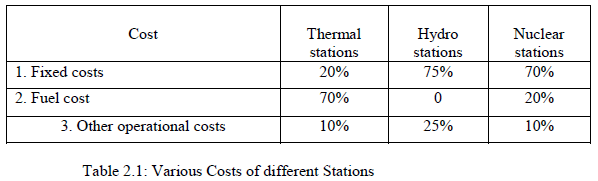image
Obviously the cost of fuel form the major portion of all variable costs and the purpose of economic operation is to reduce the cost of fuel. This is a static optimization problem. This project deals with the economic load dispatch of the thermal plants.

2.3 Generator Operating Cost Curves
The major component of the generator operating cost is the fuel input/hour, while maintenance contributes only to a small extent. The fuel cost is meaningful incase of thermal and nuclear stations. But for the hydro station where the energy storage is „apparently free‟, the operating cost of such is not meaningful.
The different operating cost curves are:
i. Input output curve.
ii. Incremental fuel cost curve.

i. Input Output Curve
The input output curve of a unit can be expressed in million kilocalories per hour or directly in terms of Rs./hour versus output in megawatts. The cost curve can be determined experimentally. A typical curve is shown in the fig. Where (MW)min is the minimum-loading limit below which it is uneconomical to operate the unit and (MW)max is the maximum output limit. By fitting a suitable degree polynomial, an expression for operating cost can be written as Fi(Pgi) Rs/hr at output (Pgi)
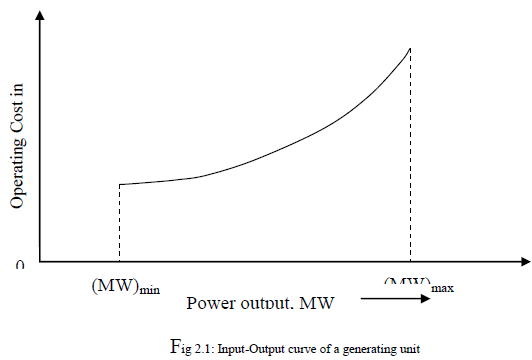image
Where the suffix i stands for the unit number. It is generally sufficient to fit a second-degree polynomial i.e.
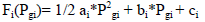image
Significance: It specifies efficiency and cost of fuel used per hour as a function of power Generation.

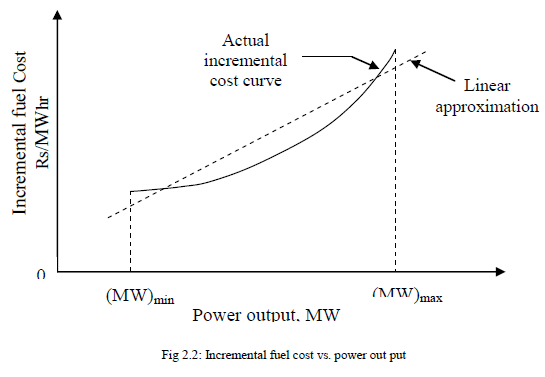
ii. Incremental Fuel Cost Curve
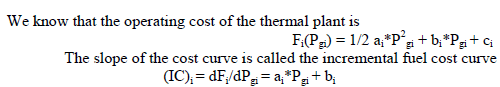image
image
It is expressed in terms of Rs/MWhr. A typical plot of this curve is shown above.For better accuracy incremental fuel cost may be expressed by a number of short line segments (piecewise linearization) alternatively we can fit a polynomial of suitable degree to represent IC curve in the inverse form equation.
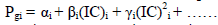image
Significance: The curve represents the increase in cost rate per increase in one mega watt output.

2.6 Economic Load Dispatch Problem

2.6.1 Economic Dispatch
The objective of economic load dispatch of electric power generation is to schedule the committed generating unit outputs so as to meet the load demand at minimum operating cost while satisfying all units and operational constraints of the power system.
The economic dispatch problem is a constrained optimization problem and it can be mathematically expressed as follows:
image

2.6.4 Network Losses
Since the power stations are usually spread out geographically, the transmission network losses must be taken into account to achieve true economic dispatch. Network loss is a function of unit generation. To calculate network losses, two methods are in general use. One is the penalty factors method and the other is the B coefficients method.
The latter is commonly used by the power utility industry. In the B coefficients method, network losses are expressed as a quadratic function:
PL = PmBmnPn
Where, Bmn are constants called B coefficients or loss coefficients.

ECONOMIC LOAD DISPATCH USING LAMBDA ITERATION METHOD
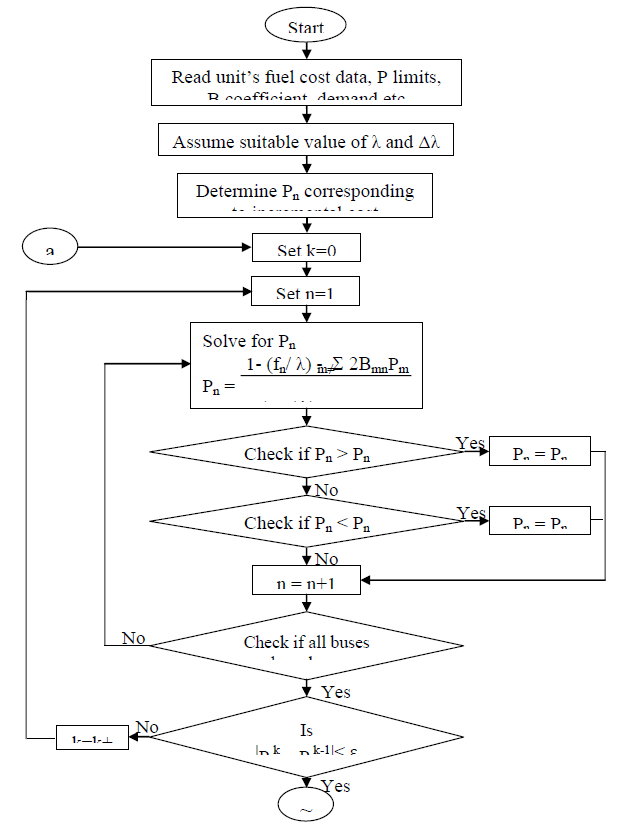
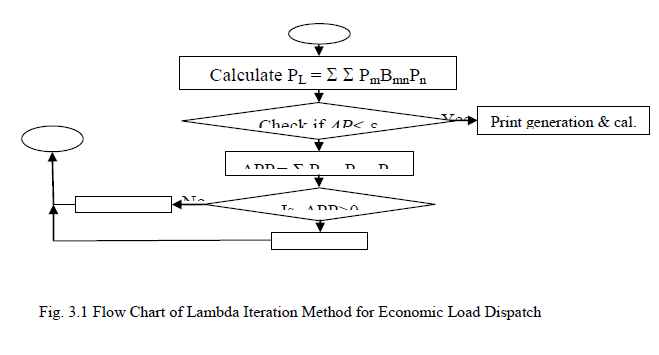
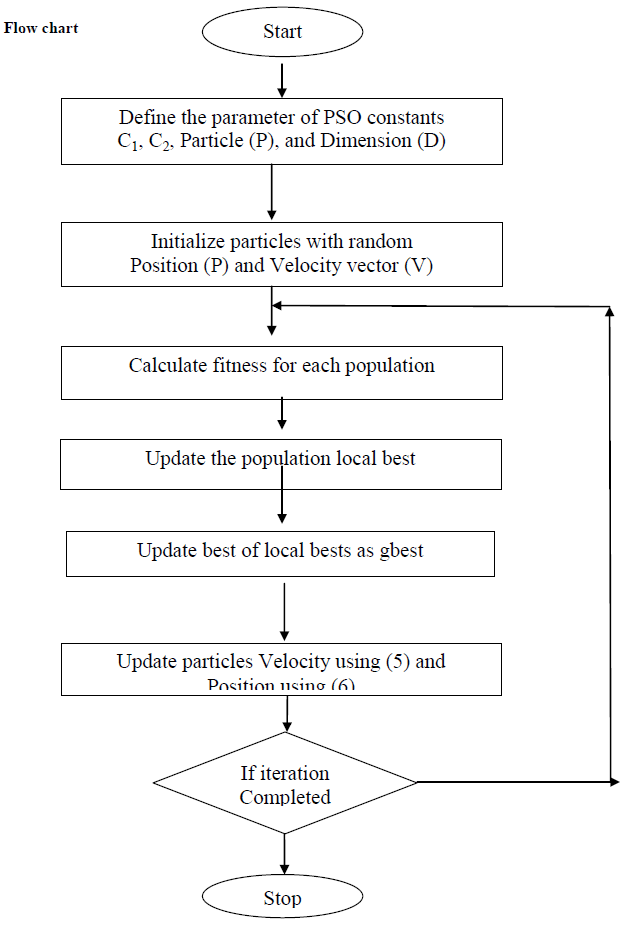
The detailed Algorithm for solving the economic load dispatch problem using lambda iteration method is given below
image

Flow Chart
image
image

PARTICLE SWARM OPTIMIZATION
image
Step 10: The individual that generates the latest gbest is the optimal generatiopower of each unit with the minimum total generation cost.
image

MATLAB
% PURE ECONOMIC DISPATCH PROBLEM USING LAMBDA ITERATION METHOD
clear all
clc
opf=fopen('lamb_eco.doc','w+');
no_units=6;
Pd=1450;
a=[0.0070 0.0095 0.0090 0.0090 0.0080 0.0075];
b=[7 10 8.5 11 10.5 12];
c=[240 200 300 150 200 120];
Pmax=[500 200 300 150 200 120];
Pmin=[100 50 80 50 50 50];
B=[ 0.000017 0.000012 0.000007 -0.000001 -0.000005 -0.000002
0.000012 0.000014 0.000009 0.000001 -0.000006 -0.000001
0.000007 0.000009 0.000031 0.000000 -0.000010 -0.000006
-0.000001 0.000001 0.000000 0.000024 -0.000006 -0.000008
-0.000005 -0.000006 -0.000010 -0.000006 0.000129 -0.000002
-0.000002 -0.000001 -0.000006 -0.000008 -0.000002 0.000150 ];
itermax=1000;
epsilon=0.1;
alpha=2*a;
clc
Pg=zeros(no_units,1);
del_lambda=0.010;
tic;deltaP=10;iter=0;
EPd=Pd/no_units;
while abs(deltaP)>epsilon && iter< itermax
iter=iter+1;
for i=1:no_units
sigma=B(i,:)*Pg-B(i,i)*Pg(i);
Pg(i)=(1-(b(i)/lambda)-(2*sigma))/(alpha(i)/lambda+2*B(i,i));
if Pg(i)<Pmin(i)
Pg(i)=Pmin(i);
end
if Pg(i)>Pmax(i)
Pg(i)=Pmax(i);
end
end
P_loss=Pg'*B*Pg;
Pt=sum(Pg);
deltaP=Pt-Pd-P_loss;
error(iter)=deltaP;
if deltaP>0
lambda=lambda-del_lambda;
end
if deltaP<0
lambda=lambda+del_lambda;
end
opf,'\n Optimal Lambda = %g\n',lambda);
for i=1:no_units
fprintf(opf,'\n Pgen(%d)=%g MW',i,Pg(i));
end
fprintf(opf,'\n Total Power Generation, P_total = %g MW\n',Pt);
fprintf(opf,'\n Total Power Demand = %g MW',Pd);
fprintf(opf,'\n Total Power Loss = %g MW',P_loss);
fprintf(opf,'\n\n Error= %g\n',deltaP);
Ft=0.0;
for i=1:no_units
F(i)=c(i)+b(i)*Pg(i)+a(i)*Pg(i)*Pg(i);
fprintf(opf,'\n Fuel cost of Gen.(%d)= %g Rs/Hr',i,F(i));
Ft=Ft+F(i);
end
fprintf(opf,'\n Total fuel cost= %g Rs/Hr\n',Ft);
runtime=toc;
fprintf(opf,'\n CPU time = %g sec.\n\n',runtime);
fclose('all')
5.1 Code for particle swarm optimization
% Particle swarm optimization
clear all;
clc;
opf=fopen('pso_eco.doc','w+');
no_units=6;
Pd=1200;
a=[240 200 300 150 200 120];
b=[7 10 8.5 11 10.5 12];
c=[0.0070 0.0095 0.0090 0.0090 0.0080 0.0075];
pmax=[500 200 300 150 200 120];
pmin=[100 50 80 50 50 50];
B=[ 0.000017 0.000012 0.000007 -0.000001 -0.000005 -0.000002
0.000012 0.000014 0.000009 0.000001 -0.000006 -0.000001
0.000007 0.000009 0.000031 0.000000 -0.000010 -0.000006
-0.000001 0.000001 0.000000 0.000024 -0.000006 -0.000008
-0.000005 -0.000006 -0.000010 -0.000006 0.000129 -0.000002
-0.000002 -0.000001 -0.000006 -0.000008 -0.000002 0.000150 ];
no_part=60;
itermax=1000;
alpha=b;
beta=2*c;
for i=1:no_units
Lambda_min(i)=alpha(i)+beta(i)*pmin(i);
Lambda_max(i)=alpha(i)+beta(i)*pmax(i);
end
lambda_min=min(Lambda_min);
lambda_max=max(Lambda_max);
lambda_min=lambda_min';
lambda_max=lambda_max';
for i=1:no_part
part(i)= unifrnd(lambda_min,lambda_max);
end
Pbest=zeros(1,no_part);
vel_max=(lambda_max-lambda_min)/10;
for i=1:no_part
vel(i)= unifrnd(-vel_max,vel_max);
end
c1=2;
c2=2;
psi=c1+c2;
K=2/abs(2-psi-sqrt(psi*psi-4*psi));
Gbest=0.0;
P=zeros(no_part,no_units);
tic;
for iter=1:itermax
for i=1:no_part
for k=1:no_units
temp=0;
for j=1:no_units
if j~=k
temp=temp+B(k,j)*P(i,j);
end
end
end
temp=2*temp;
for j=1:no_units
Nr(j)=1-(alpha(j)/part(i))-temp;
Dr(j)=(beta(j)/part(i))+(2*B(j,j));
if P(i,j)>pmax(j)
P(i,j)=pmax(j);
end
if P(i,j)<pmin(j)
P(i,j)=pmin(j);
end
end
P_loss=0;
for k=1:no_units
for j=1:no_units
P_loss=P_loss+(P(i,k)*B(k,j)*P(i,j));
end
end
Pgen(i)=0.0;
for j=1:no_units
Pgen(i)=Pgen(i)+P(i,j);
end
error(i)=Pgen(i)-Pd-P_loss;
fit(i)= 1.0/(100.0+abs(error(i))/Pd);
if Pbest(i)<fit(i)
Pbest(i)=fit(i);
Pbest_part(i)=part(i);
end
if Gbest<Pbest(i)
Gbest=Pbest(i);
Gbest_part=Pbest_part(i);
end
Wmin=0.4;
Wmax=0.9;
W=Wmax-((Wmax-Wmin)*iter/itermax);
vel(i)=K*(W*vel(i)+c1*rand()*(Pbest_part(i)-part(i))+c2*rand()*(Gbest_part-part(i)));
if abs(vel(i))>vel_max
if vel(i)<0.0
vel(i)=-vel_max;
end
if vel(i)>0.0
vel(i)=vel_max;
end
end
tpart=part(i)+vel(i);
for k=1:no_units
ttemp=0;
for j=1:no_units
if j~=k
ttemp=ttemp+B(k,j)*P(i,j);
end
end
end
ttemp=2*ttemp;
for j=1:no_units
Nr(j)=1-(alpha(j)/tpart)-ttemp;
Dr(j)=(beta(j)/tpart)+2*B(j,j);
if tp(j)>pmax(j)
tp(j)=pmax(j);
end
if tp(j)<pmin(j)
tp(j)=pmin(j);
end
end
tP_loss=0;
for k=1:no_units
for j=1:no_units
tP_loss=tP_loss+(tp(k)*B(k,j)*tp(j));
end
end
tpgen=0.0;
for j=1:no_units, tpgen=tpgen+tp(j);
end
terror=tpgen-Pd-tP_loss;
Error(iter)=terror;
tfit= 1.0/(1.0+abs(terror)/Pd);
if tfit>fit(i)
part(i)=tpart;
Pbest(i)=tfit;
Pbest_part(i)=part(i);
end
if Gbest<Pbest(i)
Gbest=Pbest(i);
Gbest_part=Pbest_part(i);
end
end
if abs(terror)<0.01
break;
end
end
runtime=toc;
fprintf(opf,'\n ECONOMIC DISPATCH USING PSO\n');
fprintf(opf,'\n Problem converged in %d iterations\n',iter);
fprintf(opf,'\n Optimal Lambda= %g\n',Gbest_part);
for j=1:no_units
fprintf(opf,'\n Pgen(%d)= %g MW',j,tp(j));
end
fprintf(opf,'\n Total Power Generation = %g MW\n',sum(tp));
fprintf(opf,'\n Total Power Demand = %g MW',Pd);
fprintf(opf,'\n Total Power Loss = %g MW\n',tP_loss);
fprintf(opf,'\n Error= %g\n',terror);
total_cost=0.0;
for j=1:no_units
Fuel_cost(j)=a(j)+b(j)*tp(j)+c(j)*tp(j)*tp(j); total_cost=total_cost+Fuel_cost(j);
end
for j=1:no_unitsfprintf(opf,'\n Fuel cost of Gen.(%d)= %g Rs/Hr',j,Fuel_cost(j));
end
fprintf(opf,'\n Total fuel cost= %g Rs/Hr\n',total_cost);
fprintf(opf,'\n cpu time = %g sec.',runtime);
fclose('all');
Using the Trust-Worthy algorithm it defines a threshold value to the SUs to overcome the PUE attacks. It enables CRNetworks nodes to efficiently utilize the available spectrum channels. Nodes, which can easily find various licensed channel opportunities without interfering the primary system increases. This reveals that it has a potential to be able to convert the various network conditions into a performance improvement.

RESULTS
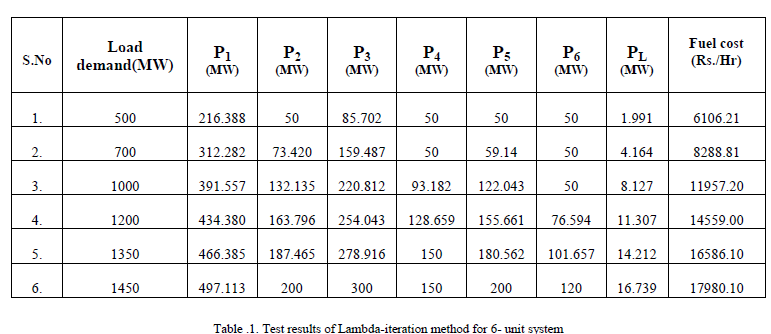
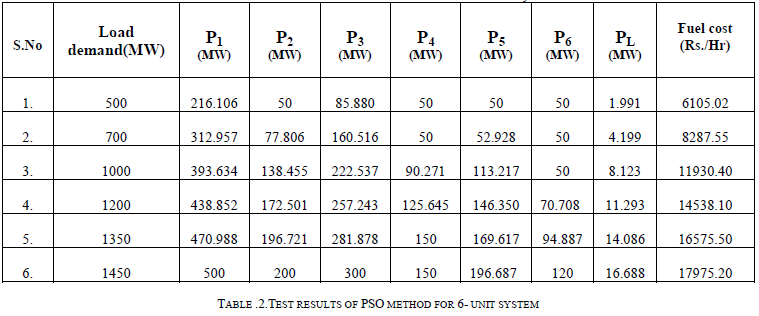
The effectiveness of the proposed method is tested with six generating units system. There are two methods used for solving the Economic load Dispatch. Firstly the problem is solved by conventional Lambda iterative method. Then a proposed PSO method is applied to solve the problem. A reasonable loss coefficients matrix of power system network was employed to draw the transmission line loss and satisfy the transmission capacity constraints. The program is written in MATLAB software.The generator cost coefficients; generation limits and B- coefficient matrix of six units system are taken from [4].These Parameters are shown in Appendix-I. The Economic Load Dispatch solution for the six-unit system is solved using conventional technique (lambda-iteration) and PSO technique and then results are compared. The results of Economic Load dispatch using Conventional method and PSO are shown in Table 1. and Table 2. for 500MW, 700MW, 1000MW, 1200 MW, 1350MW and 1450MW
image
image

CONCLUSIONS AND FUTURE SCOPE
By economic dispatch means, to find the generation of the different units in a plant so that the total fuel cost is minimum and at same time the total demand and losses at any instant must be met by the total generation. The classical optimizations of continuous functions have been considered. Various factors like optimal dispatch, total cost, incremental cost of delivered power, total system losses, loss coefficients and absolute value of the real power mismatch are evaluated for a simple system by hand calculation. The MATLAB programs were developed to solve Economic Load Dispatch Problem of an n-unit Plant through lambda iterative method and Particle Swarm Optimization. The results for the individual methods are tabulated in the previous section. From the results it can be concluded that, the lambda iterative method heavily depends on the selection of initial value. If the initial guess value is far from the actual value, i t takes much time to provide converged solution. Sometimes, the solution may not converge. In other words, the convergence of lambda iteration method depends on initial guess of lambda. Whereas PSO method always provides converged solution which does not require initial value of lambda. In this work, the ramp rate constraints are not included. Also the concept of prohibited zones is not incorporated. In future work, this can be extended by incorporating prohibited zones along with ramp rate constraints

References