Research and Reviews - International Journals

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Real Time Face Tracking By Using Naïve Bayes Classifier

Krishna Priya Arni1 , Satish Ammuloju2, Jagan Mohan Vithalachari Gollapalli3, Dinesh Bhogapurapu4 and Shaik Azeez5
  1. Student, Department of ECE, Lendi Institute of Engineering And Technology, Vizianagaram, India
  2. Student, Department of ECE, Lendi Institute of Engineering And Technology, Vizianagaram, India
  3. Student, Department of ECE, Lendi Institute of Engineering And Technology, Vizianagaram, India
  4. Student, Department of ECE, Lendi Institute of Engineering And Technology, Vizianagaram, India
  5. Assistant professor, Department of ECE, Lendi Institute Of Engineering And Technology, Vizianagaram, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

In this paper we have taken up the challenge of real time face tracking. Earlier online tracking algorithm is used for this purpose. This algorithm is data dependent. This algorithm samples the frame and separates pixels into two categories. There occurs a drawback in this method as while comparing pixels these might be a chance of wrong pixels getting matched(the pixels of face portion might get matched with pixels of back ground) and there by error in face recognition might occur. In this project we use “naive-bayes” theorem in order to overcome this drawback. The naive-bayes theorem is a theorem of probability which logically evaluates boundary conditions for matching pixels and thus helps in tracking face aptly. By using multi-scale filters and sparse matrix unwanted pixels can be eliminated thus achieving compression. Hence, using multi-scale filters, sparse matrix and naive-bayes theorem we are implementing “Real time face tracking”.

INTRODUCTION
Even though there exists numerous algorithms that have been proposed tracking remains a challenging problem due to appearance change caused by pose, illumination, occlusion, and motion, among others. An effective appearance model is of prime importance for the success of a tracking algorithm that has been attracting much attention in recent years [1–10]. Tracking algorithms can be generally categorized as generative [1, 2, 6, 10, 9] and discriminative [3– 5, 7, 8] based on their appearance models. Generative tracking algorithms typically learn a model to represent the target object and then use it to search for the image region with minimal reconstruction error. Despite the improvement, the computational complexity of several trackers is rather high, thereby limiting its applications in real-time image feature space based on compressive sensing theories [12, 13]. It has been demonstrated that a small number of randomly generated linear measurements can preserve most of the salient information and scenarios. This has been further extended by using the orthogonal matching pursuit algorithm for solving the optimization problems efficiently in Li et al. [9]. Despite these advancements still there exist several practical issues. First, numerous training samples cropped from consecutive frames are required in order to learn an appearance model online. Since there are only a few samples at the outset, most tracking algorithms often assume that the target appearance does not change much during this period. However, if the appearance of the target changes significantly at the beginning, the drift problem is likely to occur. Second, when multiple samples are drawn at the current target location, it is likely to cause drift as the appearance model needs to adapt to these potentially misaligned examples [8]. Third, these generative algorithms do not use the background information which is likely to improve tracking stability and accuracy.
Discriminative algorithms pose the tracking problem as a binary classification task in order to find the decision boundary for separating the target object from the background. There are certain methods which are developed to separate background and target of an image using positive and negative samples, still there occur problems due to noise and misaligned samples which often leads to the tracking drift problem. Later in [7,8,11]ref. different approaches for reducing the drift problem were proposed .The major problem with online tracking can be understood from the following figure.
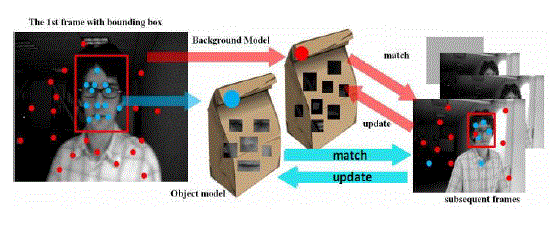In this paper, we propose an effective and efficient tracking algorithm with an appearance model based on features extracted in the compressed domain. The main components of our compressive tracking algorithm are shown below which generative as the object can be well represented is based on the features extracted in the compressive domain and also discriminative because we use these features to separate the target from the surrounding background via a naive Bayes classifier. In our appearance model, features are selected by an information-preserving and non-adaptive dimensionality reduction from the multi-scale space based on compressive sensing theories.
It has been demonstrated that a small number of randomly generated linear measurements can preserve most of the salient information and allow almost perfect reconstruction of the signal if the signal is compressible such as natural images or audio [12–14]. We use a very sparse measurement matrix that satisfies the restricted isometric property [15], thereby facilitating efficient projection from the image feature space to a low-dimensional compressed subspace. For tracking, the positive and negative samples are projected (i.e., compressed) with the same sparse measurement matrix and discriminated by a simple naive Bayes classifier learned online. The proposed compressive tracking algorithm runs at real-time and performs favorably against state-of-the-art trackers on challenging sequences in terms of efficiency, accuracy and robustness

PROPOSED ALGORITHM
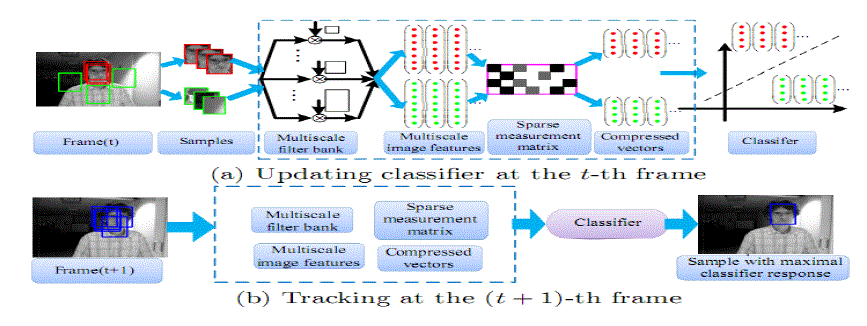
In this section, we present our tracking algorithm in details. The tracking problem is formulated as a detection task and our algorithm is shown in Figure. We assume that the tracking window in the first frame has been determined. At each frame, we sample some positive samples near the current target location and negative samples far away from the object center to update the classifier. To predict the object location in the next frame, we draw some samples around the current target location and determine the one with the maximal classification score.

Classifier Construction and Update :
For each sample z ε Rm, its low-dimensional representation is v = (v1, . . . , vn)_ ∈ Rn with m _ n. We assume all elements in v are independently distributed and model them with a naive Bayes classifier [22],
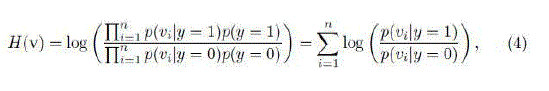image
where we assume uniform prior, p(y = 1) = p(y = 0), and y ∈ {0, 1} is a binary variable which represents the sample label. Diaconis and Freedman [23] showed that the random projections of high dimensional random vectors are almost always Gaussian. Thus, the conditional distributions p(vi|y = 1) and p(vi|y = 0) in the classifier H(v) are assumed to be Gaussian distributed with four parameters
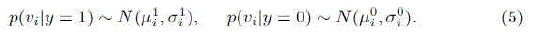image
The scalar parameters in (5) are incrementally updated
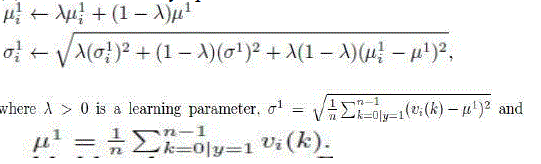image
The above equations can be easily derived by maximal likelihood estimation.
Figure 3 shows the probability distributions for three different features of the positive and negative samples cropped from a few frames of a sequence for clarity of presentation. It shows that a Gaussian distribution with online update using (6) is a good approximation of the features in the projected space. The main steps of our algorithm are summarized in algorithm 1.

Algorithm for Tracking:
Input: t-th video frame
• Sample a set of image patches, Dγ = {z|||l(z) − lt−1|| < γ} where lt−1 is the tracking location at the (t-1)-th frame, and extract the features with low dimensionality.
• Use classifier H in (4) to each feature vector v(z) and find the tracking location It with the maximal classifier response.
• Sample two sets of image patches Dα = {z|||l(z) − lt|| < α} and Dδ,β = {z|δ <||l(z) − lt|| < β} with α < δ < β.
• Extract the features with these two sets of samples and update the classifier parameters according to (6).
Output: Tracking location lt and classifier parameters

DISCUSSION
It is known that while making any advancement, simplicity is the prime characteristic and so is our algorithm. In this algorithm the proposed sparse measurement matrix R is independent of any training samples, thereby resulting in a very efficient method. In addition, our algorithm achieves robust performance as discussed below.

Difference with Related Work:
It should be noted that our algorithm is different from the other algorithms in aspects such as
• It requires only matrix multiplications while the rest requires tedious salvations to be done.
• Earlier there are algorithms which are generative models that encode an object sample by sparse representation of templates using _1-minimization, which results in cropping the training samples from the previous frames, storing and updating, but this is not required in our algorithm as we use a data-independent measurement matrix.
• Our algorithm extracts a linear combination of generalized Haar-like features but these trackers [10][9] use the holistic templates for sparse representation which are less robust.

Robustness to Ambiguity in Detection
Ambiguity is caused when the target moves fast or when its appearance changes too quickly to recognize. Multiple instance learning schemes have been introduced to alleviate the tracking ambiguity problem. Proposed algorithm is robust to the ambiguity problem. The most “correct” positive samples are similar in most frames. Whereas , the less “correct” positive samples are different as they involve some background information. Thus, the distributions for the features extracted from the most “correct” positive samples are more concentrated than those from the less “correct” positive samples which makes the features from the most “correct” positive samples much more stable than those from the less “correct” positive samples. In addition, our measurement matrix is data-independent and no noise is introduced by misaligned samples.

Robustness to Occlusion
Each feature in the proposed algorithm is spatially localized which is less sensitive to occlusion than holistic representations. Similar representations, have been shown to be more effective in handling occlusion. Moreover, features are randomly sampled at multiple scales by our algorithm in a way similar to [27, 8] which have demonstrated robust results for dealing with occlusion.
• The proposed algorithm is robust for conditions:
• Scale, Pose and Illumination Change
• Occlusion and Pose Variation
• Out of Plane Rotation and Abrupt Motion
• Background Clutters

Implementation
1. Initially images(frames) are considered which are further divided into samples. These samples are further classified as target(fore ground) and back ground samples
2. The multi scale filter bank splits or categorizes these samples into multiple components. These components are then represented in the form of a matrix.
3. These matrices are then transformed as sparse measurement matrix which avoids or eliminates least significant information.
4. These vectors are then inspected for positive probabilities using naïve bayes classifier. Using this method more positive probabilities are considered which helps in tracking desired object efficiently.

CONCLUDING REMARKS
In this paper, we proposed a simple yet robust tracking algorithm with an appearance model based on non-adaptive random projections that preserves the structure of original image space. A very sparse measurement matrix was adopted to efficiently compress features from the foreground targets and background ones. Our algorithm combines the merits of generative and discriminative appearance models to account for scene changes which enables this algorithm to perform well in terms of accuracy, robustness, and speed.
 

Figures at a glance
Figure 1 Figure 2
Figure 1 Figure 2
 

References