This paper aims at finding the value of number of clusters in advance and to increase the overall performance of K-means algorithm. Although there are various methods for removing the disadvantages of k-means algorithm as the main problem is how to calculate the value of number of clusters in advance, secondly how to remove noisy data and outliers etc. There are many solutions also for eliminating these limitations as we have used various methods and validity indexes for but in this paper we are using the matrix method for removing these problems. Experiments show that this method provides very effective results.
Keywords |
| K Means Algorithm, Clustering Analysis, Cluster, Centroid |
INTRODUCTION |
| Data Mining refers to the mining or discovery of new information in terms of patterns or rules from vast amounts of
data. Data mining is a process that takes data as input and outputs knowledge. One of the earliest and most cited
definitions of the data mining process, which highlights some of its distinctive characteristics, is provided by Fayyad,
Piatetsky-Shapiro and Smyth (1996), who define it as “the nontrivial process of identifying valid, novel, potentially
useful, and ultimately understandable patterns in data.”Some popular and widely used data mining clustering
techniques such as hierarchical and kmeans clustering techniques are statistical techniques and can be applied on high
dimensional datasets [1]. |
CLUSTER ANALYSIS |
| Cluster analysis divides data into meaningful or useful groups (clusters). If meaningful clusters are the goal, then the
resulting clusters should capture the “natural” structure of the data. For example, cluster analysis has been used to
group related documents for browsing, to find genes and proteins that have similar functionality, and to provide a
grouping of spatial locations prone to earthquakes. However, in other cases, cluster analysis is only a useful starting
point for other purposes, e.g., data compression or efficiently finding the nearest neighbors of points. Whether for
understanding or utility, cluster analysis has long been used in a wide variety of fields: psychology and other social
sciences, biology, statistics, pattern recognition, information retrieval, machine learning, and data mining.[2]Cluster
analysis groups objects (observations, events) based on the information found in the data describing the objects or their
relationships. The goal is that the objects in a group will be similar (or related) to one other and different from (or
unrelated to) the objects in other groups. The greater the similarity (or homogeneity) within a group, and the greater
the difference between groups, the “better” or more distinct the clustering. The definition of what constitutes a cluster
is not well defined, and, in many applications clusters are not well separated from one another. Nonetheless, most
cluster analysis seeks as a result, a crisp classification of the data into non-overlapping groups. [3] Fuzzy clustering, is
an exception to this, and allows an object to partially belong to several groups. We stress once again that the definition
of what constitutes a cluster is imprecise, and the best definition depends on the type of data and the desired results. |
K-MEANS CLUSTERING |
| K-means algorithm is one of the best known and most popular algorithms [3]. This algorithm was proposed by Mac
Queen. It is one of the simplest unsupervised learning algorithms that solve the clustering problem. It’s simple
procedure is to classify the dataset into number of clusters. [4]The main idea is to define k centroids, one for each
cluster. These centroids should be placed in such a way that different locations give different results. So, the better
choice is to place them as much as possible far away from each other. |
Working |
| Working of k-means algorithm is to define k centroids, one for each cluster. These centroids should be placed in such a
way that different location give different result. So, the better choice is to place them as much as possible far away
from each other. The next step is to take each point belonging to a given data set and associate it to the nearest
centroid. When no point is pending, the first step is completed. At this point need to re-calculate k new centroids[5].
After these k new centroids, a new binding has to be done between the same data set points and the nearest new centroid. Finally, this algorithm aims at minimizing an objective function, in this case a squared error function. The
objective function |
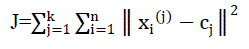 |
Where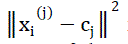 is a chosen distance measure between a data point xi
(j)and the cluster centre ���� ,is an indicator of
the distance of the n data points from their respective cluster centers. The algorithm is composed of the following is a chosen distance measure between a data point xi
(j)and the cluster centre ���� ,is an indicator of
the distance of the n data points from their respective cluster centers. The algorithm is composed of the following |
| steps: |
| 1. Place K points into the space represented by the objects that are being clustered. These points represent initial
group centroids. |
| 2. Assign each object to the group that has the closest centroid. |
| 3. When all objects have been assigned recalculate the positions of k centroids. |
| 4. Repeat Steps 2 and 3 until the centroids no longer move. This produces a separation of the objects into groups
from which the metric to be minimized can be calculated his non hierarchical method initially takes the number of
components of the population equal to the final required number of clusters. In this step itself the final required
number of clusters is chosen such that the points are mutually farthest apart. Next, it examines each component in
the population and assigns it to one of the clusters depending on the minimum distance. The algorithm is
significantly sensitive to the initial randomly selected cluster centers. The k-means algorithm can be run multiple
times to reduce this effect. |
K-means Clustering Algorithm |
| 1. Decide on a value for k. |
| 2. Initialize the k cluster centers (randomly, if Necessary). |
| 3. Decide the class memberships of the N objects by assigning them to the nearest cluster center. |
| 4. Re-estimate the k cluster centers, by assuming the Memberships found above are correct. |
| 5. If none of the N objects changed membership in the last iteration, exit. otherwise go to 3. |
Problems with K-means |
| The user has to choose the value of K, the number of clusters (some flexibility in the determination of the number of
clusters). Although for 2D data this choice can easy be made by visual inspection, it is not so for higher dimension data,
and there are usually no clues as to what number of clusters might be appropriate. Choosing an inappropriate number
of clusters will lead to a meaningless typology. For a given K, clusters will usually depend heavily on the initial
configuration of the set of centroids, thus making interpretation of the clusters rather uncertain. K-means is an objective
technique, meaning that it minimizes a quantitative criterion. It is therefore an optimization technique[6]. As is usually
the case in optimization, K-means will stop when it cannot make the value of the criterion decrease anymore, but it is
quite possible that there exist other configurations of the centroids that would yield even lower values of the criterion.
In the vocabulary of optimization, K-means reaches a local minimum, but cannot guarantee to reach
the global minimum (lowest possible value) of the criterion. |
Advantages |
| Relatively Efficient. |
| Often terminates at a local optimum. The global optimum may be found using technique such as: deterministic
annealing and genetic algorithms. |
Disadvantages |
| Applicable only when mean is defined, then what about categorical data? |
| Need to specify k, the number of clusters, in advance |
| Unable to handle noisy data and outliers |
| Not suitable to discover clusters with non convex shapes. |
Need for K |
| The originality of this algorithm is based on the fact that the conventional K-means Algorithm considers no initial
finding of the number of clusters, which makes the this advantage of k-means algorithm. This is the main limitation of
k-means that we have to specify the number of clusters in advance. Previous algorithm is not capable of determining
the appropriate number of clusters and depends upon the user to identify this in advance. |
SOLUTION STRATEGY |
| The new algorithm is formulated by matrix method in the original K-Means algorithm by calculating the Euclidean
distance between all the points in the matrix. To solve the determination of number of clusters, I used the concept of
matrix method in order to find the clustering results. A proposed K-means (PKM) clustering algorithm has been
presented. We can apply this algorithm on any type of application or any dataset. In this method, first we will take a dataset and then apply this matrix method on that. By taking a matrix form, we will calculate the distances between all
the objects of dataset by taking Euclidean distance metric as distance measure. On the basis of that calculated distance,
now in each row we will store the minimum value. By using this minimum value we will start doing clustering by
taking each object one by one. When we start this procedure from first object, it will take the value of that object in its
same cluster which has the minimum value in its row. There are two cases in this: |
| 1. If that object hasn’t come already, then it will be in same cluster with the object having minimum distance. |
| 2. If that object with least distance has come already in any cluster then the compared object will be in different
cluster. |
| Now, by taking all the clusters one by one, we will calculate the mean of every cluster. Now again use the same
procedure as in step 1 and make the clusters. From this algorithm, we will get the number of clusters in advance. By
this work, we have remove the disadvantage of k-means algorithm. Now we can easily apply this algorithm on any
dataset or application and obtain the required results. |
Dataset Setup |
| Our studies are confined to a simple k-means algorithm. However, every time k-means algorithm works well for every
dataset when we enter our choice that how many clusters we want to make. But the performance of this algorithm
degrades when its disadvantages comes. so for removing that disadvantage we are using a matrix method which will
directly calculate the value of k in advance. Data can be varied in this algorithm but this proposed algorithm works well
only with 2-dimensional datasets. Data can be taken from any datasets. We have taken six datasets here for evaluating
the results. These are: |
| 1.) (2,1)(5,7)(8,2)(3,1)(5,6)(7,2)(9,2)(4,5) |
| 2.) (1,2)(5,6)(7,8)(9,1)(2,1)(3,2)(8,1)(4,2)(4,5)(7,7) |
| 3.) (1,1)(2,1)(2,5)(9,1)(5,5)(3,3)(5,7)(4,4)(4,7)(8,1) |
| 4.) (1,1)(1,4)(6,7)(6,9)(3,3) |
| 5.) (2,1)(2,2)(3,1)(5,3)(5,4)(5,5) |
| 6.) (1,1)(1,2)(2,1)(2,2)(4,2)(5,1)(5,2) |
CONCLUSION |
| Our aim is to design a method that completely finds the value of k in advance and requires less number of iterations for
getting better quality clusters. Previously there were various methods for this problem but all are with some limitations.
They require some modifications in their format. So, we have proposed this algorithm by using matrix method that
removes the limitation of k-means algorithm. This method is simple and efficient for assigning the data points to
clusters. It also eliminates the possibility of generating empty clusters or noisy data. It requires less number of iterations
as compared to other methods. At last, it generates high quality clusters. |
| |
Figures at a glance |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
 |
 |
 |
| Figure 5 |
Figure 6 |
Figure 7 |
|
| |
References |
- IEEEI.T Jolliffe, ?Principal Component Analysis?, Springer, second edition.
- Davy Michael and Luz Saturnine, 2007. Dimensionality reduction for active learning with nearest neighbor classifier in text categorization problems, Sixth International Conference on Machine Learning and Applications, pp. 292-297
- Bradley, P.S., Fayyad, U.M., 1998. Refining initial points for K-means clustering. Proc. 15th Internat. Conf. on Machine Learning (ICML?98).
- Cheung, YM., 2003. k*-Means: A new generalized k-means clustering algorithm. Pattern Recognition Lett. 24, 2883-2893.
- Khan, S.S., Ahmad, A., 2004. Cluster center initialization algorithm for K-means clustering. Pattern Recognition Lett. .
- Growe, G.A., 1999. Comparing Algorithms and Clustering Data: Components of The Data Mining Process, thesis, department of Computer Science and Information Systems, Grand Valley State University.
- RM Suresh, K Dinakaran, P Valarmathie,?Model based modified k-means clustering for microarray data?.
|