This project proposes scheduling methods to reduce the burst transmission errors between the wireless nodes. Transmission errors are rectified by decreasing the chances of root fading. Best afford path is proposed to handle root fading and to decrease the transmission errors. This method overcomes the problem of network misbehavior that is not addressed in CNC but concentrates in NUM. We also use honey comb algorithm to extend the CNC initiated to the source node throughout the network for other nodes depending upon the network type and thus improving the mechanism when the size of network increases; scalability.
INTRODUCTION |
| Wireless sensor networks (WSNs) find important applications in environment, habitat, and infrastructure monitoring. The
main task of the sensors is to periodically generate readings and transmit them to the sink. However, sensor networks are
featured with highly unreliable links [3], and most sensors need multi-hop relay to reach the sink. Both factors contribute to
the high loss rate of data transmission, and make it very challenging for the sink to obtain high-fidelity sensor readings
under stringent energy constraint. In order to exploit the broadcast nature of wireless medium and to combat loss, network
coding has been applied in wireless multi-hop networks. |
| In particular, MORE has demonstrated that intra-flow coding can efficiently increase throughput. However, traditional
network decoding has an unfavorable all-or-nothing effect. Suppose the source has m blocks of original data. Then, in order
to recover the original data, the destination should receive at least m linearly independent blocks. If less than m blocks are
received, then almost none of the original blocks can be recovered. When the energy budget is not sufficient, the source has
to decrease its sensing rate (i.e. decrease m) in order to ensure reliability. However, decreasing sensing rate may lose
important information and affect data fidelity. Compressive network coding (CNC) is to address the tradeoff between
sensing rate and data transmission reliability. The source may generate data at desired rate, but instead of transmitting
original sensor readings, the source generates random projections of the readings (or so called measurements), and
broadcast them to its neighbors. The relay nodes perform similar random projection operation to generate new
measurements. This process of re-projection can be considered as a generic type of network coding and therefore the
proposed scheme is called compressive network coding. Finally, the sink will receive m measurements. According to the
compressive sensing (CS) theory, the data reconstruction from m random measurements is nearly as good as the best m
term approximation. Therefore, the sink is able to recover the original data with soft threshold (i.e. at different
precisions).But CNC is sensitive in Burst transmission error. So thereby scheduling method is proposed between the nodes.
And also Honey comb method is used to increase the scalability. |
RELATED WORK |
CS for Sensor Data Gathering |
| The central idea behind CS is that an n-dimensional compressible (sparse) signal can be recovered from a small number of
random linear projections. CS can potentially be applied to reduce traffic or increase throughput. A distributed compressed sensing (DCS) framework for sensor data compression. DCS exploits both intra-signal (temporal) and inter-signal (spatial)
correlations to reduce the volume of sensor readings, but the transmission problems are not considered in the work. The
main contributions lie on how to reconstruct sensor data when abnormal readings exist or sensor readings are not correlated
in adjacent neighborhood. Applying CS to exploit sensor data spatial correlations is only valid for large-scale networks.
This is because; CS works best for high dimensional signals. In small-scale sensor networks without stringent delay
constraint, CS can be used to exploit the temporal correlations to improve the data gathering precision. They proposed
compressive data gathering (CDG) in a large-scale WSN. The main contributions lie on how to reconstruct sensor data
when abnormal readings exist or sensor readings are not correlated in adjacent neighbourhood. The objective of
compressive data gathering is two-fold: compress sensor readings to reduce global data traffic and distribute energy
consumption evenly to prolong network lifetime. Similar to distributed source coding, the data correlation pattern shall be
utilized on the decoder end. Besides, compression and routing are decoupled and therefore can be separately optimized. The
intuition behind CDG is that higher efficiency can be achieved if correlated sensor readings are transmitted jointly rather
than separately. The sensor readings are combined while being relayed along a chain-type topology to the sink.. Data
gathering and reconstruction of CDG are performed on the sub-tree basis. |
| CDG is first proposed for snapshot data collection in single-radio single-channel WSNs. The basic idea of CDG is to
distribute the data collection load uniformly to all the nodes in the entire network. We take the data collection on a path
consisting of L sensors s1, s2, . . . , sL and one sink s0 as shown in Figure as an example to explain CDG. The packet produced at sensor sj (1 ≤ j ≤ L) is dj . In the
basic data collection shown in Figure (a), s1 transmits one packet d1 to s2, s2 transmits two packets d1 and d2 to s3, and
finally all the packets on the path are transmitted to s0 by sL. Obviously, nodes near the sink has more transmission load
compared with nodes far from the sink in the basic data collection. To balance the transmission load, the authors in [1]
proposed the CDG method as shown in Figure (b). Instead of transmitting the original data directly, s1 multiplies its data
with a random coefficient ��i1 (1 ≤ i ≤ M), and sends the M results ��i1d1 to s2. Upon receiving ��i1d1 (1 ≤ i ≤ M) from s1,
s2 multiplies its data d2 with a random coefficient ��i2 (1 ≤ i ≤ M), adds it to ��i1d1, and then sends ��i1d1 + ��i2d2 as one
data packet to s3. Finally, s does the similar multiplication and addition and sends the result Σ��ijdj (1 ≤ i ≤ M) to s0. After
s0 receives all the M packets, s0 can restore the original packets based on the compressive sampling theory [1]. By CDG, all the sensors send M packets to their parent nodes, which achieves the goal to uniformly distribute the data collection task
to the entire network. The number of the transmitted packets is O(n2) in Figure (a) and is O(NM) in Figure (b), and usually
M ≪ n for large scale WSNs. Therefore, CDG reduces the number of the transmitted packets. |
EXISTING SYSTEM |
Data and Network Model |
| The source may generate data at desired rate, but instead of transmitting original sensor readings, the source generates
random projections of the readings (or so called measurements), and broadcast them to its neighbors. The relay nodes
perform similar random projection operation to generate new measurements. This process of re-projection can be
considered as a generic type of network coding and therefore the proposed scheme is called compressive network coding. |
Consider a wireless sensor network with collection of sensors Si, i = 1, 2...40. Each sensor has a collection of sensor readings denoted by
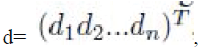 , to report to the sink. It is believed that d is compressible in a certain domain Ψ
which is known to the sink but may not be known to the sensor. The compressibility is defined as follows. Denote Ψ =
[ψ1ψ2...ψn], ψi ∈ R^n, i = 1, 2, ...n as a set of ortho normal basis. Expand d in the Ψ basis: , to report to the sink. It is believed that d is compressible in a certain domain Ψ
which is known to the sink but may not be known to the sensor. The compressibility is defined as follows. Denote Ψ =
[ψ1ψ2...ψn], ψi ∈ R^n, i = 1, 2, ...n as a set of ortho normal basis. Expand d in the Ψ basis: |
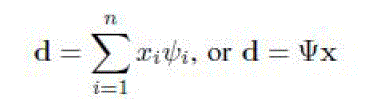 |
| Let us sort the transform coefficients {xi}, i = 1...n in descending order according to their absolute values and obtain {xi1,
xi2 ...xin}. The best k-term approximation of d, denoted by d^(k), is define as: |
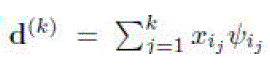 |
| Each sensor can communicate with the sink and other sensors through highly unreliable links. Denote li as the delivery ratio
from sensor Si to sink D, and denote lij as the delivery ratio between sensor Si and Sj . Then li, lij << 1. In such a network,
multi-path routing is allowed to fully exploit the broadcast nature of wireless medium. |
CNC AS A JOINT SOURCE AND NETWORK CODING SCHEME |
| CNC accomplishes joint source and network coding through the same random projection operation. In the process of
source s generates a matrix of random coefficients, denoted by Φs or {φsij}, and produces m measurements: |
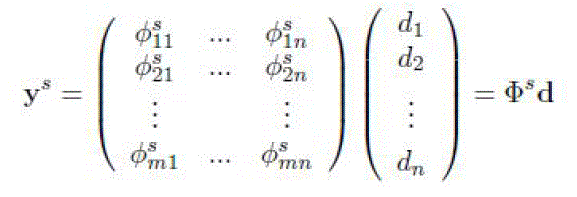 |
| When d is compressible, m is smaller than n. Therefore, transmitting the measurements consumes less energy than
transmitting the original readings. |
| Random re-projection is performed at each intermediate node to increase diversity. Suppose node r decides to relay mr
measurements for source s, it then randomly generates the new measurements with: |
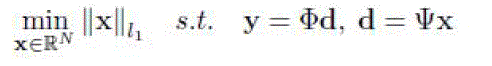 |
| where Φr is an mr × ms,r random matrix. The value of mr is decided by a distributed utilization optimization algorithm.
Finally, the sink receives m_ messages, possibly from multiple paths. The entire random projection based joint
sourcenetwork coding process can be described by: |
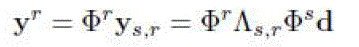 |
| where ΦN represents the network coding coefficients and Φs represents the source coding coefficients. |
| When d is sparse or compressible, it can be perfectly reconstructed from y under certain conditions. According to
CS theory, data reconstruction can be achieved through solving l1-minimization problem: |
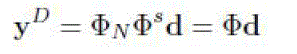 |
| It is known that can be computed by linear programming. It stated that the average squared error of CS reconstruction from
m random projections is upper bounded by a constant times (m/log n)^−2α, nearly as good as the best m-term
approximation. |
| In order to solve, matrices ΦN and Φs should be known to the sink. The overhead of transmitting ΦN matrix in CNC is
the same as that in conventional random linear network coding. A commonly adopted approach is to include the network
coding coefficients in each transmission block. It has pointed out, the relative overhead of transmitting these coefficients
decreases with increasing length of blocks over which the codes and network remain constant. Matrix Φs does not need to
be transmitted with data packets. It can be obtained by the following process: before data transmission, the sink broadcasts
a random seed to the entire network. Then, each sensor generates its source coding matrix using this global seed and its
unique identification. With the same pseudo random number generator, the sink can reproduce the source coding matrices
for all sensors. Finally our existing system shows delivery ratio with 60% for 40 nodes in network. |
Network Coding and Network Utility Maximization |
| The idea of network coding is first proposed in error-free wired network for single source multicast to achieve
network capacity. MORE performs intra-flow network coding in a wireless multi-hop network. Network coding ensures
that multiple nodes that hear the same transmission do not forward the same packet. The combination of random network
coding and opportunistic routing efficiently exploits the broadcast nature of wireless medium and combats losses |
Network utility maximization for CNC flows |
| In monitoring sensor networks, all sensors collect data and create multiple concurrent flows. Each sensor node,
while being the source of its own flow, may also relay data for other sources. Most sensors even need to relay data for
multiple flows. Therefore, we shall address the network utility maximization (NUM) issue for CNC flows. In this research,
special emphasis is put to tackle the high unreliability of sensor communications. At this point, we do not explicitly bring in
MAC constraint in our NUM formulation, because the transmission energy, not wireless medium, is the main constraint of
a data gathering network. |
Demerits |
| CNC is sensitive in burst transmission error. |
| CNC is used for source nodes alone
Scalability is restricted |
PROPOSED WORK |
Scheduling |
| When the source is requested by two different destinations operating in different bandwidths a deadlock like condition
occurs which produces congestion at the source level. To avoid this problem have to schedule the data based on bandwidth
lifetime. Design a network with n nodes with a constant bandwidth and increase the throughput for each transmission.
Observe the following: |
| • TTL of the active link |
| • Maximum data transferred |
| The source is requested by two different destinations operating in different bandwidths, deadlock condition occurs. It
raises congestion at the source level. To avoid this problem, have to schedule the data based on bandwidth lifetime and
message type. |
Honey Comb Method |
| The HC method is proposed to extend the CNC to other nodes in a network. In a homogenous network CNC can be
extended to destination node other than source. In a heterogeneous network, the CNC can be implied to intermediate node
other than source and destination. HC is a spreading mechanism. It opts the routing path to reach the other nodes. It
supports directed, bi-directional and random paths for improving the states. When a network size varies, HC opts a routing
and can be extended. Thus it supports scalability. As the drawback of scalability is overcome in HC implemented network,
unobservability and out of range problem are minimized in a network |
CONCLUSION AND FUTURE WORK |
| In the existing system they have presented a CNC framework for sensor data gathering which unifies source coding and
network coding under the same random projection operation. We have formulated a NUM problem, and have designed a
practical distributed algorithm for flow allocation at controlled energy budget. Simulations over real sensor data have
shown that CNC is not working in burst transmission errors. In this paper, scheduling method is proposed to reduce the
burst transmission error and Honey Comb method is used to increase scalability. In this research, we exploit the temporal
correlations in sensor readings. In the future, this CNC to exploit both temporal and spatial correlations among sensor
readings, to achieve potentially higher compression ratio and shorter latency. |
| |
Figures at a glance |
 |
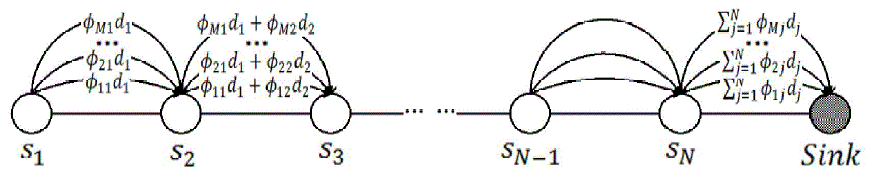 |
| Figure 1a |
Figure 1b |
|
| |
References |
- N. Nguyen, D. L. Jones, and S. Krishnamurthy, ?Netcompress: Coupling network coding and compressed sensing for efficient data communication in wsns,? in IEEE Workshop on SiPS, pp. 356?361, Oct. 2010.
- C. Luo, F. Wu, J. Sun, and C. W. Chen, ?Compressive data gathering for large-scale wireless sensor networks,? in Proc. of ACM Mobicom?09, pp. 145?156, Sep. 2009.
- X. Zhang and B. Li, ?Dice: a game theoretic framework for wireless multipath network coding,? in ACM Mobihoc, pp. 293?302, May 2008.
- W. Wang, M. Garofalakis, and K. Ramchandran, ?Distributed sparse random projections for refinable approximation,? in Proc. of IPSN, pp. 331?339, April 2007.
- N. Nguyen, D. L. Jones, and S. Krishnamurthy, ?Netcompress: Coupling network coding and compressed sensing for efficient data communication in wsns,? in IEEE Workshop on SiPS, pp. 356?361, Oct. 2010.
|