Keywords
|
| Cloud computing, peer to peer system, measuring data availability, data redundancy removal. |
INTRODUCTION
|
| Most of these services offer users clean and simple storage interfaces, and details of the actual location and management of resources will be hidden. Current cloud storage infrastructures are focused on providing users with easy interfaces and high performance services. However, the current cloud model for some classes of storage services may not suited well. For example, consider a research institute that wishes to freely share its results with others institutions as a ‘‘public service’’, but it requires deployment resources. Since the service deployers may not want to pay the cost of running the service because it may not be commercial. |
| Heterogeneity will be one of the major challenges of cloud computing platforms in the future [1]. Unfortunately, existing storage solutions [2, 3, and 4] have considered homogeneous settings, where all nodes are treated equal regarding their on-line/off-line behavior. Such clouds built of heterogeneous hosts such as nebulas and distributed data centers. |
| Goals: The aim of the paper is to reduce data redundancy by considering the heterogeneous node availabilities in cloud storage system. |
| To reduce the data redundancy, it should be able to |
| • Accurate measure of data availability; |
| • To identify the optimal quantity of information to be assigned to each host; and |
| • To identify the minimum data redundancy that maintains the targeted data availability. |
| The 3 main contributions are |
| 1. We develop an analytical framework to compute data availability in heterogeneous environments. Since it is computationally costly to calculate the data availability when the set of storage nodes grows, we propose a Monte Carlo method to estimate the real value in a less computational expensive way. |
| 2. Since determining the optimal amount of redundancy to be assigned at each host is computationally hard, we propose a novel heuristic based on particle swarm optimization (PSO) [9]. From our results, we infer a simple allocation function to optimally find the minimum redundancy required. |
| 3. Finally, we provide a simple iterative algorithm to determine the minimum redundancy required to guarantee the data availability requirements of different possible storage applications. |
RELATED WORK
|
| By reducing redundancy, distributed storage systems can reduce storage and communication costs. However, there is a theoretical limit [6] beyond which communication costs cannot be reduced without increasing storage costs. |
Peer- to- peer storage system
|
| Peer-to-peer systems can be characterized as distributed systems in which all nodes have identical capabilities and responsibilities and all communication is symmetric. To guarantee the data, the data redundancy is the main key. However, preserving redundancy in the face of highly dynamic membership is costly. For this, redundancy scheme of replication and erasure coding has been proposed. This results show that, when average node availability is higher than 48% it requires more storage space and replication scheme saves more bandwidth than erasure coding scheme. |
| The main objective of this paper is to optimize distributed storage systems by considering the real heterogeneities present in cloud [7] systems, or any other existing distributed systems. More specifically, we focus on reducing redundancy by considering the individual online/offline patterns of nodes. In [8], Deng and Wang considered node heterogeneities in grid storage systems. However, they did not exploit such heterogeneities to reduce the amount of data redundancy required. To the best of our knowledge, we are the first to exploit node heterogeneities in that way. In this paper, we propose additional algorithms to extend our results to any node set size. |
DATA STORAGE MODEL
|
| Throughout this paper, we will consider a distributed storage system working in its steady state: the number of nodes and the number of stored objects is kept constant. Let H represent the set of all storage nodes. Then, these process stores each data object in a small subset of nodes, N; In this work we do not treat how nodes in N are chosen. A possible solution is to ask to a centralized directory service for a list of nodes with free storage capacity. However, we will consider that N is a random sample of H for the sake of simplicity. Then We will analyze the impacts of the size of |N. Additionally, let us denote by a A(t) and U (t) the two subsets of N containing respectively the available and unavailable nodes at time t. Clearly, N=A (t) U U (t); for all t>= 0. Using erasure codes, the storage process needs to decide which the redundancy is required to store each data object r. so the storage process generates a large ‘‘pool’’ of redundant blocks. Finally, these blocks are scattered and stored using the nodes in N. The storage process sets the values of n to a static value and then varies k to obtain different redundancy ratio than the different data availabilities. |
| The storage process can work in three different ways according to the size of N and the value of n |
| 1. n > |N|: There are more redundant blocks than storage nodes. The storage process has to decide to which nodes store more blocks. |
| 2. n = |N|: There are exactly the same numbers of data blocks than storage nodes. The storage process stores one data block to each node. |
| 3. n < |N |:When comparing to storage node, these are less data blocks. We can consider this case as having a smaller set of storage nodes N0 where n = |N0| because some nodes will not have storage blocks. |
PROBLEM STATEMENT
|
Existing storage systems do not consider the individual node availabilities, i a and use the mean node availability as the basis of their models. The mean node availability is given by, 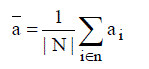 |
| Here all nodes are treated equally without considering the heterogeneities, and then, the assignment function stores to all nodes the same number of redundant blocks. For homogeneous conditions, storage systems assume n=|N|. Then, the assignment function becomes g (i) =1; for all n. |
| In this paper, we study the impact of considering real availabilities in distributed storage systems and how this heterogeneity could be exploited to reduce the amount of redundancy required to achieve the desired availability: Here the methodology will be divided in three main steps: |
| 1. In heterogeneous scenario, providing an analytical framework to measure real data availability, d, |
| 2. Designing an assignment function g for a given fixed data redundancy, which maximizes d. |
| 3. Finding the minimum data redundancy that guarantees that the data availability obtained is greater than the desired one, d ≥ d |
MEASURING DATA AVAILABILITY
|
| In this section, we provide the basic framework to measure data availability, d, in a specific storage scenario. As we previously defined, data availability is a probabilistic metric that depends on several parameters. Among all these parameters, we are interested in measuring d as a function of: (1) the erasure code’s parameters k and n, (2) the assignment function g and (3) the set of nodes N. Hence, to measure data availability we obtain a function, D, such that, d= D (k, n, g, N).We define D for a generic heterogeneous environment. We can measure d for all possible combinations of heterogeneous nodes by using this expression. However, due to its inherent complexity, this function cannot be used when the set of storage nodes N contains more than 20 nodes, |N| > 20. We provide two simplifications of the generic expression applicable fewer than two different assumptions. On the one hand, we give an expression for a scenario where heterogeneities nodes are not considered.e.g. Heterogeneities nodes are not considered when all node availabilities are very similar. On the other hand, we simplify give the expression for heterogeneous environments where node’s can be represented by a small collection of values clustered availabilities. Then finally, when these assumptions cannot be used, we propose a Monte Carlo algorithm to approximate d for any set of storage nodes. |
Assuming heterogeneous node availabilities
|
Let the power set of N, 2 N denote the set of all possible combinations of online nodes. Let also A, A ? 2 n represent one of these possible combinations. Then, we will refer as QA to the event that the combination A occurs. Here node availabilities are not dependent, so we have that:  |
| Additionally, let Lk, Lk ∈ 2 N , be the subset containing those combinations of available nodes with that used store k different redundant blocks , |
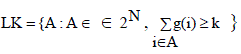 |
| Let us consider the simplest scenario where g(i)= 1 ∀i∈ N, and n =|N|.This means that measuring data availability using the heterogeneous generic expression has a O ( 2n ) complexity. Because of this, it is unfeasible to measure with expression in real applications using large N sets. This measurement does not finish in less than an hour for storage sets larger than 20 nodes in a typical desktop computer. |
Assuming homogeneous node availabilities
|
| Assumption 1 (Homogeneous assumption): As we described above when we consider homogeneous node availabilities, we assume that n =|N| and that each node is storing exactly one data block, g(i)= 1 ∀i∈ N.Considering the Homogeneous Assumption, we can redefine (in this particular case) Lk, so Lk = {A: A ∈ N; |A| ≥ k } Remark 1 (Mean node availability): In the homogeneous case a i = a,∀i∈N where a is the mean node availability defined. Under Homogeneous Assumption, the complexity of the data availability measurement, d, could be significantly reduced. First of all, we use above to restate as, |
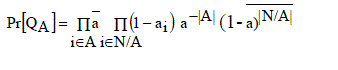 |
Clustering availability
|
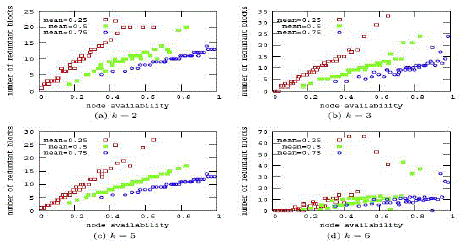
| Data availability can become computationally intractable for large N sets. The reason of this complexity is that all nodes have different availabilities and then, the number online nodes in different combinations are also very large. This type of complexity can be reduced when groups of nodes in N share the same online availability. Eg. Data centers built of racks with identical computers–, but nodes from different data centers have different properties. The complexity of measuring data availability d under the clustered assumption is still o(2n ) although expressions for d, heterogeneous expression and clustered expression have complexity o(2 n ) the hidden constants for the clustered case are smaller. In Fig. 1 we evaluate the computational complexity of the clustered version for different number of clusters, c, and c= |C| and we compare the number of summands required to measure d in both cases. |
| For eg, considering this in a typical desktop computer we were unable to measure d for sets larger than 20, the results show that may reduce computation time for measuring d in sets of up to 50 nodes, 4 or less clusters. Although less than 8 clusters are useful for measuring d in sets from from 20 to 50 nodes, we need other tools to measure d for larger node sets. |
Monte Carlo approximation
|
| It is unfeasible to measure the exact data availability for large heterogeneous storage sets. However, if we want to reduce redundancy by finding the optimal assignment function g and the optimal redundancy we need at least an approximate value for d. In this section, we use a Monte Carlo method to obtain this approximate value. This technique is mainly to obtain simulate the real behavior of the storage system and empirically measure the obtained data availability. |
| In this method, we randomly generate a set, sω , of ωsamples drawn from 2 N .This set contains x possible combinations of online nodes. Each combination A∈Sω is chosen considering the individual availabilities ai of each node as follows: |
| Pr [i∈A]= a i ∀ A∈Sω∀i∈N |
| By using the above notation, the approximation of the real data availability d, can be obtained as |
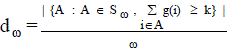 |
Algorithm 1.Measuring d ω
|
| 1. success ← 0 |
| 2. iterations ← ω |
| 3. while iterations > 0 do |
| 4. blocks ← 0 |
| 5. for i∈N do |
| 6. if rand () ≤ ai then |
| 7. blocks ← blocks + g(i) |
| 8. end if |
| 9. end for |
| 10. if blocks ≥ k then |
| 11. successes ← successes+1 |
| 12. end if |
| 13. iterations ← iterations-1 |
| 14. end while |
| 15. d ω ← successes/iterations |
FINDING OPTIMAL ASSIGNMENT FUNCTION
|
| Once we solved the problem of how to measure data availability, in this section we face the problem of how to assign the n redundant blocks in order to maximize data availability. Unlike the homogeneous case, where each node was responsible of one block, under the heterogeneous case, it is used to assign more blocks to the more stable nodes to increase data availability. However, finding the optimal data assignment function g is another hard computable task. All the possible assignments of n redundant blocks to a set of nodes, N, is like computing (in number theory) all the compositions of n are determined. This problem is known to have 2n-1 different assignments, from that determining the best assignment becomes computationally intractable for large sets of nodes N. |
| Lin et al. demonstrated in [6], that in the homogeneous case, to maximize data availability there is a trade-off between node availability and the number of nodes used. We have also noticed that in the heterogeneous finding this trade-off is key to determine the optimal assignment function g. In our scenario, we can increase the mean node availability by storing data only to the high stable nodes in N. However, this reduces the number of storage nodes used. On the other hand, in N if we are using all nodes, the mean node availability and data availability decreases. |
| Unfortunately, because of the huge number of possible assignments, we will use a heuristic optimization algorithm to find the best solution. Optimization algorithms such as search space, is to find which point in this space maximizes a specified function. The function that we want to maximize is data availability, D (k, n, g, N), and the search space is all the possible implementations of the assignment function g. First, in Section 6.1, we describe the particle swarm optimizer algorithm. Then, in Section 6.2, we define the search space required by the optimization algorithm. Finally, in Section 6.3, we conclude the results of optimal function g from the optimization’s results. |
PARTICLE SWARM OPTIMIZER ALGORITHM
|
| To find the optimal assignment function, we used a particle swarm optimizer (PSO) [9]. PSO can be applied to virtually any problem that can be expressed in terms of an objective function for which an extreme is required to be found. Information about this function is shared between particles, and then it will allow other particles to update their velocities to direct their motion towards other particles in fitter regions. We chose PSO because research results have shown that it out performs other nonlinear optimization techniques such as Simulated Annealing and Genetic Algorithms [9]. |
Algorithm 2
|
| 1:[x*] = PSO () |
| 2: P = Particle_Initialization (); |
| 3: For i=1 to it_max |
| 4: For each particle p in P do |
| 5: fp = f (p); |
| 6: If fp is better than f (pBest) |
| 7: pBest = p; |
| 8: end |
| 9: end |
| 10: gBest = best p in P; |
| 11: For each particle p in P do |
| 12: v = v + c1*rand*(pBest – p) + c2*rand*(gBest – p); |
| 13: p = p + v; |
| 14: end |
| 15: end |
| Particle update rule |
| p = p + v |
| With |
| v = v + c1 * rand * (pBest – p) + c2 * rand * (gBest – p) |
| Where |
| P: particle’s position |
| V: path direction |
| c1: weight of local information |
| c2: weight of global information |
| PBest: best position of the particle |
| gBest: best position of the swarm |
| Rand: random variable |
| The inertia weight is a user-specified parameter that controls the impact of the previous history of velocities on the current velocity. This inertia weight resolves the trade-off between the global and local exploration ability of the swarm. The inertia weight with larger value encourages global exploration (moving to previously not searched areas of the space), while a smaller one favors local exploration. |
| A suitable value for this coefficient provides the optimal balance between the global and local exploration ability of the swarm to improve the effectiveness of algorithm. Previous experimental results suggest that it is preferable to initialize the inertia weight to a large value, which is used to give the priority of global exploration of search space, and gradually decrease [10]. Consequently, we set the inertia weight using the equation: |
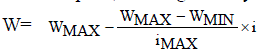 |
| Here WMAX and WMIN are the initial and final values of the inertial coefficient iMAX , the maximum number of iterations and i the current iteration. |
DEFINING THE SEARCH SPACE
|
Let R |N| be a Cartesian |N|-space that is R |N| is an affine and Euclidean |N|-dimensional space coordinated and oriented by the orthonormal affine frame 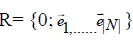 Then, assuming that N is an ordered set, the vector with all node assignments [g (i)] i?|N| , corresponds to a point p?N|N| on frame R with integer coordinates(x1, x2,…..x|N|).Each component xi corresponds to the number of redundant blocks assigned to the ith node in N. Then, assuming that N is an ordered set, the vector with all node assignments [g (i)] i?|N| , corresponds to a point p?N|N| on frame R with integer coordinates(x1, x2,…..x|N|).Each component xi corresponds to the number of redundant blocks assigned to the ith node in N. |
From the whole search space R|N| , we are only interested in a small subset of possible solutions that satisfy the requirement of the assignment function 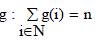 This requirement restricts the search space S to the positive area of the hyper plane This requirement restricts the search space S to the positive area of the hyper plane 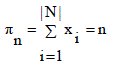 |
| Unfortunately, we cannot apply a PSO algorithm directly by randomly setting the particles in S.By allowing this, PSO would randomly update the position and velocity of each particle in all of its dimensions and cause particles to move within all R|N| generating positions out of S, and then, not compliant with the requirements of function g: particles should move within the positive area of πn .In order to solve this drawback we move the reference frame within R|N| , setting |N| -1 vectors of the new frame within the plane πn , and then, freeing particles from one degree of freedom, and keeping them always within πn . |
DERIVING FROM THE PSO RESULTS
|
| By running the PSO algorithm in several different scenarios with different set sizes and different node availabilities we can find the optimal assignment function. We set the PSO’s inertia parameters to WMIN =0.5, WMAX = 0.75 and iMAX = 50, and the constants to n1, n2:=1. We used a population of 100 particles. We can run two different experiments by using this setup. In the first experiment, small set of storage nodes |N|=10 are used and the generic analytical expression in the fitness function. In the second experiment we made use of a larger storage set |N|=100, and approximated d with the Monte Carlo method. |
| Fig. 1 shows the optimal assignment found for |N| =10, using the heterogeneous expression as the fitness function. Then we observe that optimal assignment tends to assign more redundant data to the stable nodes without discarding the low availability storage nodes. And also this assignment tends to be aligned along a line that passes through the origin of coordinates. The errors that we appreciate points separated from this line are the effect of using a non-deterministic assignment algorithm: PSO. |
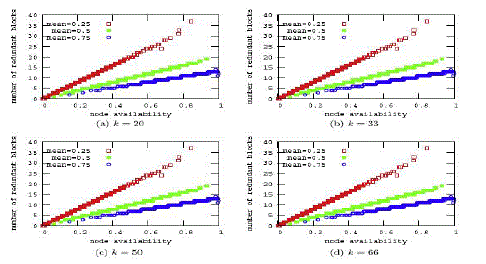
| Fig. 2 shows the same results than Fig. 1 but with a larger set of storage nodes |N | = 100, and using the Monte Carlo data availability measure as the fitness function. Although this time we used a doubled heuristic (PSO + Monte Carlo), the results tend to be analogously aligned. This time, since we used a larger set of storage nodes, the results appear less sparse. Again, some errors appear points separated from the main line because of the non-deterministic assignment algorithm: Besides, since the total amount of assigned blocks should be equal to n, |
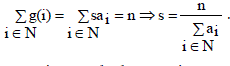 . . |
And then 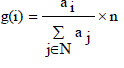 . It is the optimal assignment function derived from experimental observations. . It is the optimal assignment function derived from experimental observations. |
FINDING OPTIMAL DATA REDUNDANCY
|
| Once we know how to measure data availability and the optimal assignment function, it only remains to find the minimum amount of redundancy required to guarantee a minimum data availability d. Finding the redundancy means finding the minimum r= n/k ratio that achieves d. However, since two different parameters: k and n are involved in r, different pairs of k and n can be used to achieve d. In the existing literature, storage systems initially set k to a fixed value and increase n from n = k until they achieve the desired data availability d. Instead, in this paper we will initially set n to a fixed value n = |N|. β , for a large b, and we will decrease k from k = n until we achieve the desired availability d. By doing it we have more redundant blocks than nodes in N, and we can easily store more blocks to those more stable nodes. |
CONCLUSION AND FUTURE WORK
|
| Existing cloud storage services are designed and built based upon the homogeneous cloud storage infrastructure. This assumption simplifies the way data availability is measured, but it introduces an error that causes an increase in the data redundancy, and then, a loss in efficiency. In this paper, we have studied how disregarding heterogeneities in node availabilities affects negatively the performance of heterogeneous cloud infrastructures. The three benefits are (1) an algorithm for measuring data availability in heterogeneous storage infrastructures;(2) an optimization algorithm to find the best way to assign redundant blocks to the set of storage nodes; and (3) a mechanism to determine the minimum data redundancy to achieve a desired quality of service. We discovered that the best results come up when nodes are assigned an amount of redundancy proportional to their availabilities. We have shown how this solution can reduce data redundancy up to 70% in highly heterogeneous scenarios to consider in distributed storage infrastructures in general, and in heterogeneous clouds in particular. |
| Finally, since economic revenue is one of the key aspects of cloud storage services, we will extend our work to consider it in further works. By considering it, we could find better assignments functions to obtain storage systems not only optimal in its redundancy but also optimal in its cost and also used to reduce the execution time by Parallel Particle Swarm Optimization algorithm. |
Figures at a glance
|
 |
 |
| Figure 1 |
Figure 2 |
|
| |
References
|
- L.M. Vaquero, L. Rodero-Merino, J. Caceres, M. Lindner, A break in the clouds: towards a cloud definition, SIGCOMM Comput. Commun. Rev. 39 (1) (2009) 50?55.
- F. Wu, T. Qiu, Y. Chen, G. Chen, Redundancy schemes for high availability in dhts, in: Proceedings of the Third International Symposium on Parallel and Distributed Processing and Applications (ISPA), 2005.
- W.K. Lin, D.M. Chiu, Y.B. Lee, Erasure code replication revisited, in: Proceedings of the Fourth International Conference on Peer-to-Peer Computing (P2P), 2004.
- R. Rodrigues, B. Liskov, High availability in dhts: erasure coding vs. replication, in: Proceedings of the Fourth International Workshop on Peer-To-Peer Systems (IPTPS), 2005.
- A. Dimakis, P. Godfrey, M. Wainwright, K. Ramchandran, Network coding for distributed storage systems, in: Proceedings of the 26th IEEE International Conference on Computer Communications (INFOCOM), 2007.
- C. Blake, R. Rodrigues, High availability, and scalable storage, dynamic peer networks: pick two, in: Proceedings of the Ninth Workshop on Hot Topics in Operating Systems (HOTOS), 2003.
- R. Campbell, I. Gupta, M. Heath, S.Y. Ko, M. Kozuch, M. Kunze, T. Kwan, K. Lai, H.Y. Lee, M. Lyons, D. Milojicic, D. O?Hallaron, Y.C. Soh, Open cirrus cloud computing testbed: federated data centers for open source systems and services research, in: Proceedings of the Usenix Workshop on Hot Topics on Cloud Computing (HotCloud?09), 2009
- Y. Deng, F. Wang, A heterogeneous storage grid enabled by grid service, SIGOPS Oper. Syst. Rev. 41 (1) (2007) 7?13.
- J. Kennedy, R. Eberhart, Particle swarm optimization, in:Proceedings of the IEEE International Conference on Neural Networks, 1995.
- Y. Shi, R.C. Eberhart, Parameter selection in particle swarm optimization, in: Proceedings of the Seventh International Conference on Evolutionary Programming (EP), 1998.
- Z. Zhang, Q. Lian, Reperasure: replication protocol using erasurecode in peer-to-peer storage network, in: Proceedings of the 21st Symposium on Reliable Distributed Systems (SRDS), 2002
|