International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Reduction of Delay and Power by Using MLDD Technique in Error Correction

S.Abinaya1, Mr.M.Yuvaraja2
  1. M.E, Department of PG-ES, P.A College of Engineering and Technology, Pollachi, Tamilnadu, India
  2. HOD, Department of ECE, P.A College of Engineering and Technology, Pollachi, Tamilnadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

This project presents an error-detection method for Euclidean Geometry Low Density Parity Check codes with majority logic decoding methodology .The algorithm is synthesized in Xilinx 12.1 and simulated using Modelsim 5.7g .Majority logic decodable codes are suitable for memory applications due to their capability to correct a large number of errors. However, they require a large decoding time that impacts memory performance. The proposed fault-detection method significantly reduces the delay time by detecting the errors in parallel and in pipelining manner. Also the memory access time reduces when there is no error in the data read. The technique uses the majority logic decoder itself to detect failures, which makes the area overhead minimal and keeps the extra power consumption low. Starting from the original design of the ML decoder introduced, the proposed ML Detector/Decoder (MLDD) has been implemented.

Keywords
Error correction codes, Euclidean geometry low-density, Parity check (EG-LDPC) codes, majority logic decoding, memory.

INTRODUCTION
Error correction codes are commonly used to protect memories from so-called soft errors, which change the logical value of memory cells without damaging the circuit [1]. As technology scales, memory devices become larger and more powerful error correction codes are needed [2], [3]. To this end, the use of more advanced codes has been recently proposed [4]–[8]. These codes can correct a larger number of errors, but generally require complex decoders. To avoid a high decoding complexity, the use of one step majority logic decodable codes was first proposed in [4] for memory applications, decoded using one step majority logic decoding [9]. Further work on this topic was then presented in [5], [6], [8]. One step majority logic decoding can be implemented serially with very simple circuitry [9], but requires long decoding times. In a memory, this would increase the access time which is an important system parameter. Only a few classes of codes can be
Among those are some Euclidean geometry low density parity check (EG-LDPC) codes which were used in [4].A method was recently proposed to accelerate a serial implementation of majority logic decoding of EG-LDPC codes. The idea behind the method is to use the first iterations of majority logic decoding to detect if the word being decoded contains errors. If there are no errors, then decoding can be stopped without completing the remaining iterations, therefore greatly reducing the decoding time. For a code with block length N, majority logic decoding (when implemented serially) requires N iterations, so that as the code size grows, so does the decoding time. In the proposed approach, the errors are detected in parallel and pipelining manner. The detection process requires single iteration where most of the errors are detected. The delay time, power consumption, area for this proposed method is low compared to the previous technique.

EXISTING MAJORITY LOGIC DETECTOR/DECODING TECHNIQUE
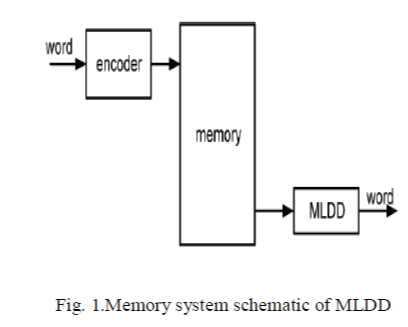
Majority Logic Detector/Decoding (MLDD) technique is generally based on number of parity check equations. These check equations are the results of XOR gates. The inputs to the XOR gates are the fifteen bit data which are stored in the shift registers.A generic schematic of memory system is depicted in Fig .1.In this Fig the input data is sent to the encoder and stored in the memory. The decoding process is done in the MLDD.
The codeword used in this technique is the EG-LDPC code (Euclidean Geometry -Low Density Parity Check).It is the One Step Majority Logic Decodable code. This code uses the check sum algorithm. The check sum algorithm is nothing but a numerical value is associated with the code word to be transmitted. Then the code word received at the receiver end has some numerical value. There is a comparison on the associated numerical values to detect the error.
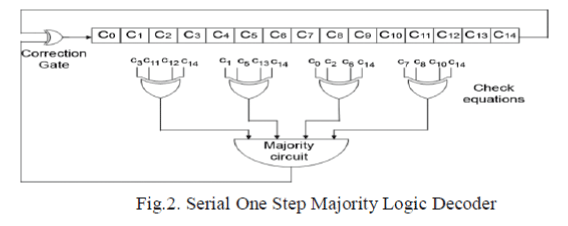
The existing method is implemented using simple hardware. The decoding time for this method is more. Also the power consumption and area requirement are high. To detect the errors serially the MLDD technique uses Serial One Step Majority Logic Decoder. The serial one step majority logic decoder is depicted in Fig.2.
In this decoder 15 bit data is first stored in the cyclic shift register. Then the inputs are assigned to the XOR gates. Since there is 15 bit data the XOR gates required are four. The bit to be detected should be given as one of the inputs for all the XOR gates. The outputs of the XOR gates are the check sum equations. The check sum equations consist of binary data.
Then the Majority circuit outputs the data which is in major number. If the output of the majority circuit is ‘1’ then the corresponding bit has the error else the bit is error free.
The output of the Majority circuit is given as one of the input to the correction gate. Another input to the correction gate is the bit which is under test. So the corrected bit is stored into the shift register where first cyclic shift occurs. This entire process is called as one iteration. Likewise three iterations are processed. Maximum number of errors is detected within these three iterations. Thus detecting error in serial manner is feasible only for three iterations. This drawback is overcome in the proposed technique.
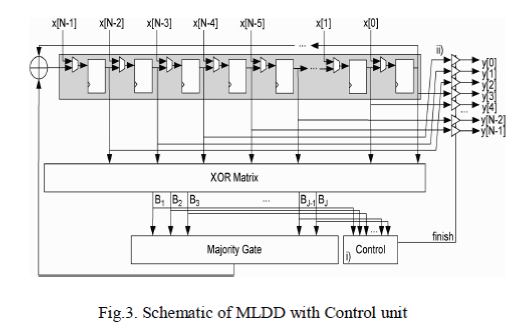
The schematic of MLDD is shown in Fig.3. It consists of cyclic shift registers, XOR matrix, Majority gate, control unit, tri state buffers and XOR gate.
In this schematic the control unit has the important characteristic. It stores the result of three iterations. After receiving the results of three iterations it sends “finish” signal to the tri state buffer which indicates the data is error free. The tri state buffer is in high state untill it receives the finish signal. After receiving the finish signal it goes low and outputs the current data from cyclic shift register. The output of the buffer is the detected data.

AREA, POWER AND DELAY ANALYSIS
From the existing method the power and delay is calculated and shown in Table I.
The area requirement for the Serial MLD technique is shown in Table II.

PROPOSED MAJORITY LOGIC DETECTOR/DECODING TECHNIQUE
In this technique the error detection process is done in parallel and in pipelining manner. The iteration required for detection is only one. Thus the delay time is comparatively low. Also the power consumption and the area requirement is low. Considering the Fig.2. The entire 15 bit data is detected simultaneously in single iteration. But the cyclic shift is same as in serial error detection process. Error detection process is also done in pipelining manner. In this process area requirement is further reduced compared to parallel processing. The results obtained using parallel processing is shown in Table III.
The area required for the Parallel Processing is shown in Table IV.

PRELIMINARIES
Finite geometries have been used to derive many error-correcting codes [9], [11]. One example are EG-LDPC codes which are based on the structure of Euclidean geometries over a Galois field. Among EG-LDPC codes there is a subclass of codes that is one step majority logic decodable (MLD) [9]. Codes in this subclass are also cyclic. The parameters for some of these codes are given in Table I, where N is the block size, N the number of information bits, N the number of MLD check equations and N the number of errors that the code can correct using one step MLD. One step MLD can be implemented serially using the scheme in Fig.2 which corresponds to the decoder for the EG-LDPC code with N. First the data block is loaded into the registers.
Then the check equations are computed and if a majority of them has a value of one, the last bit is inverted. Then all bits are cyclically shifted. This set of operations constitutes a single iteration: after N iterations, the bits are in the same position in which they were loaded. In the process, each bit may be corrected only once. As can be seen, the decoding circuitry is simple, but it requires a long decoding time if N is large. The check equations must have the following properties .
1) All equations include the variable whose value is stored in the last register
2) The rest of the registers are included in at most one of the check equations.
If errors can be detected in the first few iterations of MLD, then whenever no errors are detected in those iterations, the decoding can be stopped without completing the rest of the iterations. In the first iteration, errors will be detected when at least one of the check equations is affected by an odd number of bits in error. In the second iteration, as bits are cyclically shifted by one position, errors will affect other equations such that some errors undetected in the first iteration will be detected. As iterations advance, all detectable errors will eventually be detected. In [10] it was shown that for DS-LDPC codes most errors can be detected in the first three iterations of MLD. Based on simulation results and on a theoretical proof for the case of two errors, the following hypothesis was made.
“Given a word read from a memory protected with DS-LDPC codes, and affected by up to five bit-flips, all errors can be detected in only three decoding cycles”.
Then the proposed technique was implemented in VHDL and synthesized, showing that for codes with large block sizes the overhead is low. This is because the existing majority logic decoding circuitry is reused to perform error detection and only some extra control logic is needed.

RESULTS
The proposed method has been applied to class of one step MLD EG-LDPC codes. The results are presented with the help of simulation. For codes with small words and affected by a small number of bit flips, it is practical to generate and check all possible error combinations. As the code size grows and the number of bit flips increases, it is no longer feasible to exhaustively test all possible combinations. Therefore the simulations are done in two ways, by exhaustively checking all error combinations when it is feasible and by checking randomly generated combinations in the rest of the cases. The simulation results show the error detected in single iteration and most of the errors are detected.

CONCLUSION
In this brief, the detection of errors in single iteration using one step majority logic decoding technique is more feasible than the serial manner. Also the EG LDPC code is more advantageous than the DS LDPC.Future work includes extending the theoretical analysis to more number of errors.
 

Tables at a glance
Table icon Table icon Table icon Table icon
Table 1 Table 2 Table 3 Table 4
 

Figures at a glance
Figure 1 Figure 2 Figure 3
Figure 1 Figure 2 Figure 3
 

References