In this paper a technique called back Propagation Network (BPN) is proposed to cancel electromyogram (EMG) interference in electrocardiogram (ECG). The performance evaluation of the proposed technique is done in terms of signal to noise ratio, mean square error and epochs. The paper presented also illustrates the effect of training algorithm for a given application. Electrocardiogram signals are used to detect heart diseases and also in recent clinical studies. These signals (ECG) are mixed with noise such as baseline drift, electrode motion artifacts, power line interference etc. Previous studies for ECG noise removal are not up on satisfactory marks due to the non stationary nature of the associated noise sources and their spectral overlap with desired ECG signals.
Keywords |
| Noise removal, Electrocardiogram (ECG), Electromyogram (EMG), Back propagation (BPN), Spectral overlap. |
INTRODUCTION |
| Electrocardiogram (ECG) signals have been widely used in clinical studies for the diagnosis of heart disorders. It is the
electrical potential record produced by heart. Due to the movement of Na+ and K+ ions in blood the electrical wave is
generated by depolarization and repolarization of certain cells. The ECG signal is in the range of 2mv and also require a
recording bandwidth of 0.1 to 120 Hz [1]. To acquire ECG signal non invasive technique is used i.e. placing the electrodes
at standard location on the skin of person [2]. The ECG signal and heart rate expose the cardiac health of human heart. Any
disorder in heart rate or change in morphological pattern of ECG signal indicates cardiac arrhythmia. It is detected and
identified by analysis of recorded ECG waveform. Information about the nature of disease related to heart is contained in
amplitude and duration of the P-QRS-T-U wave. Generally the recorded ECG is often corrupted by different types of noises
and these artifacts that can be with in the frequency band of ECG signal and may change characteristics of ECG signal.
Hence it is very difficult to take out useful information of signal. The major noise that corrupt the ECG signal are
Electromyography(EMG) noise, power line interference, noise due to random movement and respirational movements,
electrode contact noise. |
| High pass, low pass, window based filter for the analysis of ECG are defined in[3]. In this rectangular, hamming, hanning,
kaiser window are used for noise reduction in ECG. The rectangular window FIR has sharpe attenuation. The rectangular
has linear phase and filter was found to be stable. Various modeling techniques are employed, such as the extended Kalman
filters [4]. RLS based adaptive filter is presented [5]. In this paper performance characteristics of two adaptive filters LMS
and RLS are given. The MSE increases and SNR decreases in RLS adaptive filter in comparison to LMS adaptive filter. |
| The performance comparison of SRLMS, NSRLMS, LMS etc. is based on SNR is in [6]. Values of SNR in this paper
shows that its value is less in basic algorithm like SRLMS as compared to NSRLMS. Same in case with LMS and NLMS,
which means that normalizing improves SNR. Discrete wavelet transform and neural network is used for ECG signal noise
reduction [7]. Neural network model for noise reduction is in [8]. In this paper neural network model is developed for noise
reduction. Two different neural networks have been compared to minimize the effect of noise. Several other techniques
have been also proposed to extract the ECG components contaminated with the background noise and allow the
measurement of subtle features in the ECG signal. |
| The rest of the paper is organized as follows: Section II is about problem formulation means what types of problems are in
previous work. After that section III for algorithm description, in which steps regarding algorithm takes place. In section IV
design methodology of network and the last Section V discuss the results and section VI concludes the paper. |
PROBLEM FORMULATION |
| • Electromyogram (EMG) artifacts often contaminate the electrocardiogram (ECG). They are more difficult to
suppress or eliminate, compared for example to the Baseline wander etc. Electromyogram is a random signal. It
varies from time to time and also from person to person. Due to their random character and to the considerable
overlapping of the frequency spectra of ECG and EMG signals obtained from the same pair of electrodes. |
| • There are many methods have been implemented to eliminate the noise from noisy signal. High pass, low pass and
notch filter are the basic method to pass the signal. The filters have the biggest disadvantage that these also remove
important frequency components in the locality of cut off frequency. The usually applied low-pass filtering results
in limited suppression of the EMG artifact and considerable reduction of sharp Q, R and S ECG wave amplitudes. |
| • ECG is a random signal. The coefficients of static filter are constant. Therefore design of static is not possible to
cancel the interference in ECG. |
| • To overcome the limitation of static filters different adaptive filtering methods are developed. The design of fixed
filter is not possible to cancel the interference in ECG. Hence, an adaptive mechanism called BPN is proposed in
this paper. It explains the efficiency of BPN to cancel the EMG interference in ECG signal. |
ALGORITHM DESCRIPTION |
| Artificial Neural Network (ANN) has been the successfully used classifier in numerous fields. So, it is of interest to use it
for ECG analysis. The basic processing unit of brain is neuron which works identically in ANN [9]. The neural network is
formed by a set of neurons interconnected with each other through the synaptic weights. It is used to acquire knowledge in
the learning phase. The number of neurons and synaptic weights can be changed according to desired design perspective.
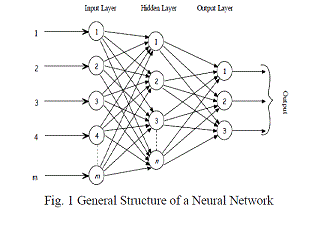
The basic neural network consists of 3 layers input layer, hidden layer, output layer.
Fig. 1 |
Back propagation network |
| The back propagation training with generalized delta learning rule is an iterative gradient algorithm designed to minimize
the root mean square error between the actual output of a multilayered feed-forward NN and a desired output. Each layer is
fully connected to the previous layer, and has no other connection. |
| The Back Propagation Algorithm is explained in the following steps: |
| Step 1 : Initialization |
| Set all the weights and biases are set to small real random values between 0 and 1. |
| Step 2 : Presentation of input and desired output |
| Present the input vector x(1), x(2), . . . , x(N)from the measured ECG signal and corresponding desired response d(1), d(2), .
. . , d(N) from original ECG signal, where N is the number of training patterns. |
| Step 3 : Calculation of actual outputs |
| Equation (1) below is used to calculate the output signals y1, y2…... yNM |
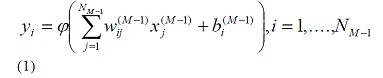 (1) (1) |
| Where |
| wij are the weights and bi are the biases. |
| Step 4: Adaptation of weights (wij) and biases (bi) |
| The weights and biases are changed as per equation (2) |
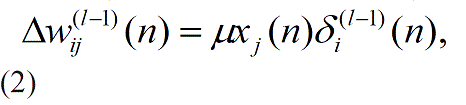 |
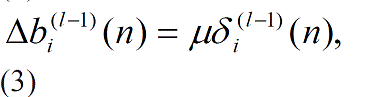 |
| Where |
 |
| in which xj (n) = output of node j at iteration n, l is layer, k is the number of output nodes of neural network, M is output
layer, φ is activation function. The learning rate is represented by μ. There are two phases of data flow. First, the input
pattern is propagated from the input layer to the output layer and, as a result of this forward flow of data, it produces an
actual output. Then the error signals resulting are back propagated from the output layer to the previous layers to update
their weights. Different training algorithms use the gradient of the performance function to determine how to adjust the
weights to minimize performance (i.e., MSE), these algorithms are Gradient descent with adaptive lr (learning rate) back
propagation (traingda), gradient descent momentum and adaptive lr back propagation (traingdx), Leverberg Marquardt back
propagation (trainlm) and Scaled conjugate gradient back propagation(trainscg) [9]. |
Implementation of BPN |
| The software used for the implementation of BPN is MATLAB. The basic procedure for implementing BPN algorithm is as
follow: |
| • Specifying the inputs and targets to the BPN. |
| • Specifying the number of layers. Repeated experiments were performed to determine the size of the hidden layer. |
| • Mentioning the activation functions for each layer: |
| TANSIG is a hyperbolic tangent sigmoid transfer function for hidden layer. |
| PURELIN is a linear transfer function which is used as the activation function for the output layer. |
| • Creating a feed forward back propagation network. |
| • Training the network using the training function called TRAINLM, TRAINSCG, TRAINGDA, and TRAINGDX. |
DESIGN METHODOLOGY |
| Various steps used for removal of noise from ECG are as follow: |
| • First collect the ECG and EMG signal. |
| • Corrupted signal in which EMG and ECG signals interfered. |
| • Calculate Estimated Signal ECG signal. |
| • Then apply back propagation with different training algorithms. |
| • Compare the performance of training algorithms. |
| • Get estimated Desired Signal. |
RESULTS AND DISCUSSION |
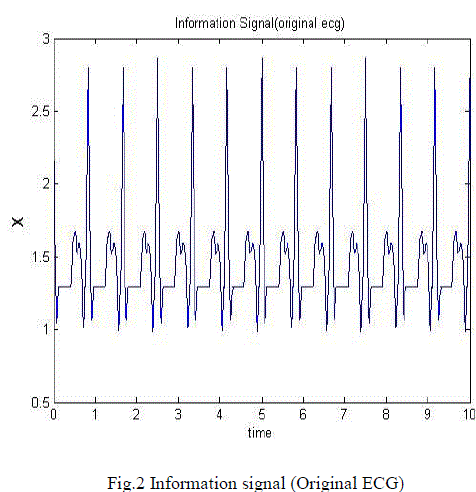
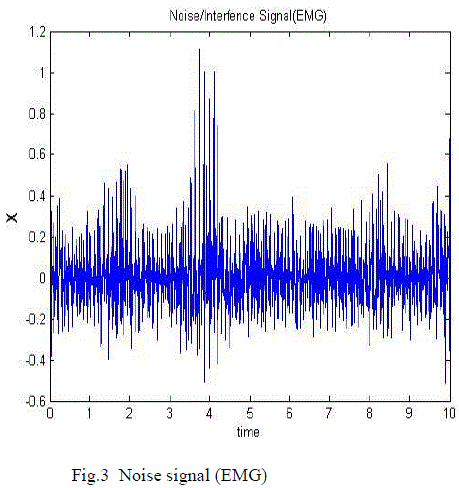
| The proposed system was evaluated using ECG signals with muscle noise (EMG). In fig. 2 original ECG signal is the target
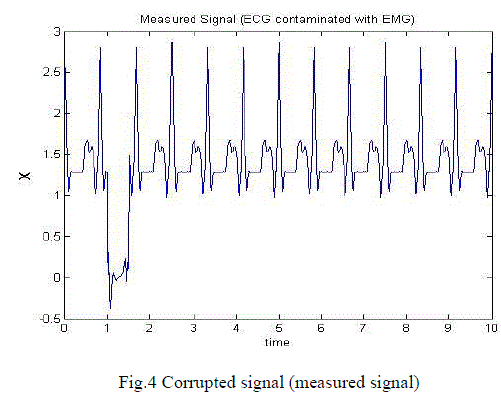
in the training process and fig. 3 shows EMG signal. In fig. 4 corrupted signal is shown in which EMG and ECG signals
interfered. The training stops as soon as the performance goal (mean square value of the estimated ECG) reaches a
minimum. Mean Squared Error is the average squared difference between outputs and targets. Lower values of (MSE)
indicate better performance of the network and zero means no error. |
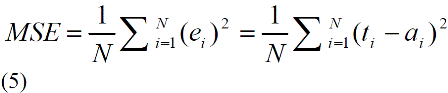 |
| |
| Where, t - Target
a - Actual output
e – Error,
N – Number of exemplars |
| Here target is to achieve the original ECG signal .which is given as a target to the network. The input to the signal is
measured signal which is contaminated with EMG signal noise. This is caused by the contraction of other muscles besides
the heart. |
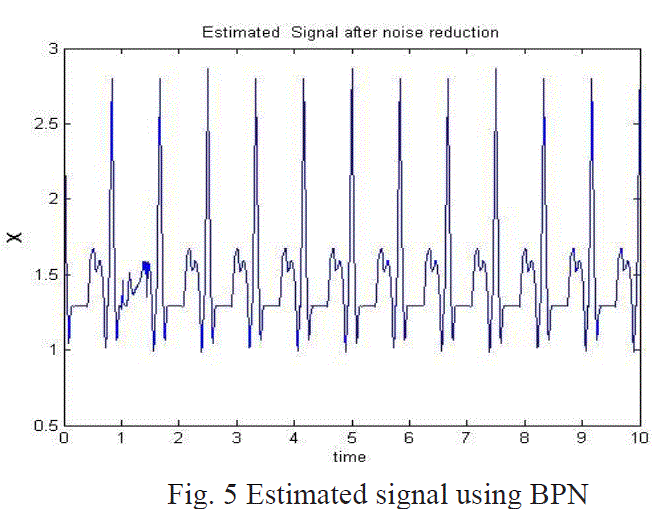
| The estimated ECG using BPN is shown in fig 5. Table 1 summarizes the results of NN's training by comparing the Elapsed
time, Epochs, SNR and the MSE with four training algorithms. These algorithms are Gradient descent with adaptive lr
(learning rate) back propagation (traingda), gradient descent momentum and adaptive lr back propagation (traingdx),
Leverberg Marquardt back propagation (trainlm), Scaled conjugate gradient back propagation (trainscg). All of these
algorithms use the gradient of the performance function to determine how to adjust the weights to minimize performance
(i.e., MSE). |
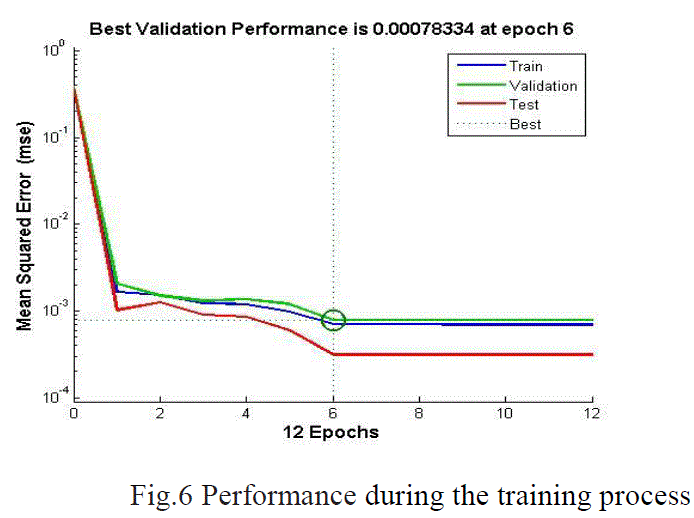
| As can be seen in Tables 1,NN trained with TRAINLM back propagation function results in a fastest algorithm
implementation (12 epochs) with a best performance (MSE equals 0.000783).The estimated ECG signal using BPN and
performance during the training process with trainlm algorithm is shown in fig. 6. |
CONCLUSION |
| The ECG signal is contaminated by various noises such as electrode noise, power line interference, and EMG.
Conventional methods are used to remove the non physiological noises. Since some of the characteristics of ECG signal are
similar to EMG signal. BPN technique is employed to cancel the EMG interference in ECG signal. The results obtained
indicate that BPN is a useful technique to cancel the nonlinear interference from the ECG signal even if the frequency
content of the interference overlaps with each other. From the above graph it is evident that the performance goal given to
the various neural network learning algorithm that works on the back propagation with highest accuracy in term of fitting
the to the pure ECG signal (original) from the noisy signal (measured). Leverberg Marquardt back propagation (trainlm)
has value of MSE is very less and take less time. |
| |
Tables at a glance |
 |
| Table 1 |
|
| |
Figures at a glance |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
 |
 |
 |
| Figure 4 |
Figure 5 |
Figure 6 |
|
| |
References |
- R. Acharya, J. S. Suri, J. A.E. Spaan and S .M. Krishnan, ?Advances in Cardiac Signal Processing?, Springer Berlin Heidelberg, New York, ISBN: 3-540-36674-1, 2007.
- J. Moss and S. Stern, ?Non-invasive electrocardiology: Clinical aspects of holter monitoring?, 1st edition,W.B. Saunders, Philadelphia, ISBN: 9- 7020-1925-9,1996.
- K. Jagtap, M.S. Chavan, R.C. Wagvekar and M.D. Uplane, ?Application of the digital filter for noise reduction in electrocardiogram?, Journal of Instrumentation, vol.40, no. 2, pp. 83?86, June 2010.
- O. Sayadi, M. Shamsollahi, ?ECG denoising and compression using a modified extended Kalman filter structure?, IEEE Trans. Biomed. Eng. 55 (9), 2240?2248, 2008.
- Sachin Singh and Dr K. L. Yadav ?Performance Evaluation Of Different Adaptive Filters For ECG Signal Processing? International Journal on Computer Science and Engineering vol. 02, No. 05, 1880-1883, 2010.
- Syed Ateequr Rehman , R.Ranjith Kumar, ?Performance Comparison of Adaptive Filter Algorithms for ECG Signal Enhancement? International Journal of Advanced Research in Computer and Communication Engineering vol. 1, Issue 2, 2012.
- Suranai Poungponsri, Xiao-Hua Yu ?An adaptive filtering approach for electrocardiogram (ECG) signal noise reduction using neural networks? Neurocomputing 117, page 206?213, 2013
- Lubna Badri ?Development of Neural Networks for Noise Reduction? The International Arab Journal of Information Technology, vol. 7, No. 3,2010.
- Demuth H. and Beale M., ?Neural Networkm Toolbox-for Use with MATLAB User?s Guide,The Mathworks, Massachusetts.?2002.
|