ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
1HOD, Dept of Information Technology, Panimalar Institute of Technology, Chennai, India
2Assistant Professor, Dept of Information Technology, Panimalar Institute of Technology, Chennai, India
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
PASTRY andOverlie routing is a very attractive scheme that allows improving certain properties of the routing (such as delay or TCP throughput) without the need to change the standards of the current underlying routing. PASTRY is an implementation of a Distributed Hash Table(DHT) algorithm for P2P routing overlay using the PASTRY implementation the silent features to achieve the reliability,fully centralized and high fault tolerant . However, deploying overlie routing requires the placement and maintenance of overlie infrastructure. This gives rise to the optimization,reliability,high fault tolerant and highly distributed problem which we overcome in this project using . PASTRY distributed algorithm and non-trivial approximation algorithm. The current BGP routing in the Internet , where from a single source to all autonomous systems (ASs), that a small number of less than 100 relay servers is sufficient to enable routing over shortest paths reducing the average path length.
PASTRY ,Non-trivial approximation algorithm; shortest path; minimum cost; end-to-end delay.
An overlie network is a computer network, which is built on the top of another network. Nodes in the overlie can be thought of as being connected by virtual or logical links, each of which corresponds to a path, perhaps through many physical links, in the underlying network. For example, distributed systems such as peer-to-peer networks and clientserver applications are overlie networks because their nodes run on top of the Internet.
Overlie routing and PASTRY computer connected to the Internet and running PASTRY node software can be a PASTRY node Application specific security policies may be applied Each node is identified by a unique 128 bit node identifier (NodeId) The node identifier is assumed to be generated randomly Each Node Id in is assumed to have the same probability of being chosen Node with similar Node Id may be geographically far Given a key , PASTRY can deliver a message to the node with the closest Node Id to key within d log2b Ne steps, where b is a configuration parameter (usually b= 4) and N is the number of nodes has been projected in modern years as an effective way to attain certain routing properties, without going into the long and tiresome process of consistency and global employment of a new routing protocol. The main and foremost main is to reduce the end to end delay which can be achieved by minimizing the number of nodes in between the sender and receiver.
Overlie Voice-over-IP (VoIP) applications such as Skype ,Google Talk , Tango, Viber and others. Such applications are becoming more and more popular offering IP telephone services for free ,but they need abounded end-to-end delay (or latency)between any pair of users to maintain a reasonable service quality. We show that our scheme can be very useful also in this case, allowing applications to choose a smaller number of hubs, yet civilizing performance for many users.
Questions like these arose like : How “good” is Internet routing from a user’s perspective considering round-trip time, packet loss rate, and bandwidth? They showed that in 30%–80% of the cases, there is an alternate routing path with better quality compared to the default routing path.
While the concept of using pastry routing and overlie routing to improve routing scheme was presented in this work, it did not deal with the deployment aspects and the optimization aspect of such infrastructure. A resilient overlie network (RON), which is an architecture for application-layer overlie routing to be used on top of the existing Internet routing infrastructure.
Similar to our work, the main goal of this architecture is to replace the existing routing scheme,high fault tolerant and achieves highly distributed .This work mainly focuses on the overlie infrastructure (monitoring and detecting routing problems,highly distributed and maintaining the reliable system), and it does not consider the cost associated with the deployment of such system.
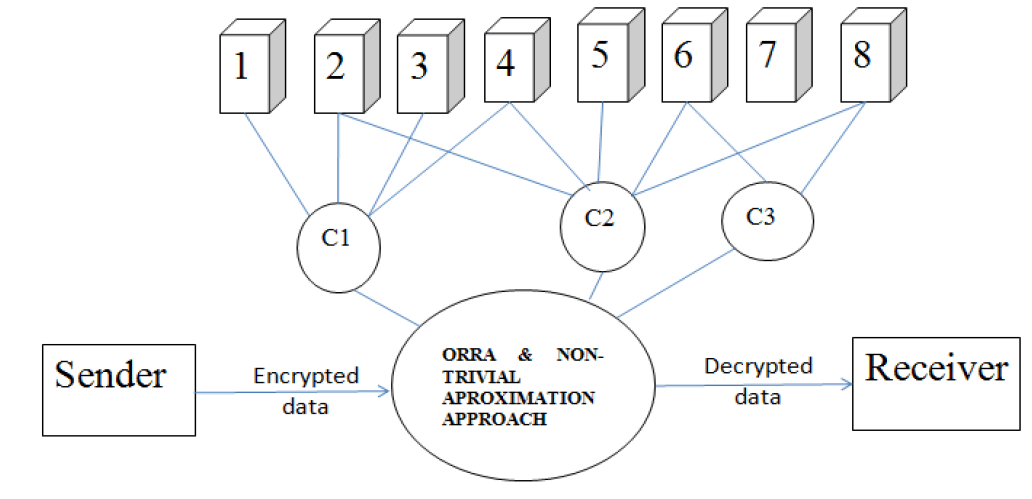
• Sender sends data in encrypted format.
• There are eight available nodes or servers.
• Out of the eight available nodes three shortest paths are found out they are C1, C2, C3.
• Non-Trivial Approximation algorithm is used to select the best shortest path.
• The Receiver decrypts the data.
• Encryption and decryption is done by using RSA Algorithm.
rsa algorithm for encrypting the data
1. Choose two different large random prime numbers 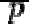 and
and 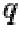
2. Calculate 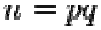
• 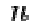 is the modulus for the public key and the private keys
is the modulus for the public key and the private keys
3. Calculate the totient: 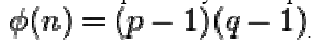
4. Choose an integer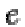 such that 1
such that 1 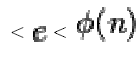 , and
, and 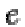 is coprime to
is coprime to 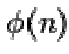 ie:
ie: 
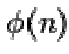 share no
factors other than 1; gcd
share no
factors other than 1; gcd 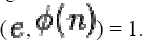
• 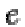 is released as the public key exponent
is released as the public key exponent
5. Compute 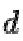 to satisfy the congruence relation
to satisfy the congruence relation 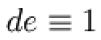
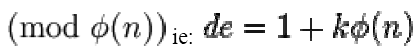 for some integer
for some integer 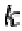 .
.
• 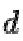 is kept as the private key exponent
is kept as the private key exponent
• Step 1: Numbers can be probabilistically tested for primality.
• Step 3: changed in PKCS#1 v2.0 to 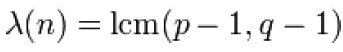 instead
of
instead
of 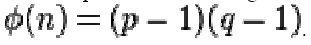
• Step 4: A popular choice for the public exponents is 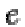 = 216 + 1 = 65537. Some applications choose smaller
values such as
= 216 + 1 = 65537. Some applications choose smaller
values such as 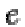 = 3, 5, or 35 instead. This is done to make encryption and signature verification faster on small
devices like smart cards but small public exponents may lead to greater security risks.
= 3, 5, or 35 instead. This is done to make encryption and signature verification faster on small
devices like smart cards but small public exponents may lead to greater security risks.
• Steps 4 and 5 can be performed with the extended Euclidean algorithm; see modular arithmetic.
The public key is made of the modulus 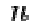 and the public (or encryption) exponent
and the public (or encryption) exponent 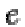 .
.
The private key is made of the modulus 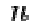 and the private (or decryption) exponent
and the private (or decryption) exponent 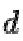 which must be kept secret.
which must be kept secret.
• For efficiency a different form of the private key can be stored:
• 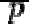 and
and 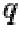 : the primes from the key generation,
: the primes from the key generation,
• 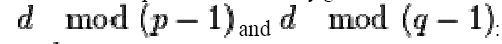 often called dmp1 and dmq1.
often called dmp1 and dmq1.
• 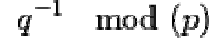
pastry & non-trivial approximation algorithm for finding the shortest path
ALGORITHM 1
State of a node Each PASTRY node has a state consisting of:
• a routing table used in the First phase of the routing (long distances)
• a neighborhood set M contains the Node Id and IP addresses of the M nodes which are closest (according to a metric) to the considered node
• a leaf set L contains the Node Id and IP addresses of the L 2 nodes whose NodeId are numerically closest smaller than the present Node id, and the L 2 nodes whose NodeId are numerically closest larger than the present Node Id The routing table is a dlog2b(N)ex(2b- 1) table
• B is the configuration parameter
• N is the number of PASTRY nodes in the network The 2 b-1 entries at row n each refers to a node whose NodeId shares the present node NodeId in the first n digits but whose (n+ 1)th digit has one of the 2b-1possible values other than (n+ 1)th digit in the present node id.
ALGORITHM 2
The routing procedure is shown in pseudocode form below. It is executed whenever a message with destId D arrives at a node with nodeId A. We begin by defining some notation.
Rii: the entry in the routing table R for domain i, 0<i<2b at level l, 0<l<b[128/b].
Mi: the entry in the neighbourhood table M, representing the jMj i-th closest node, 0_i< . Li: the i-th closest node Id in the namespace table L,-[L/2]<i<[l/2], where negative/positive indices indicate node Ids smaller/larger than the present nodeId, respectively.
Di: the domain of dest Id D at level l. shl(A,B): the length of the prefix shared among Aand B, in levels.
(2) // Dis within range of our namespace set
(3) forward to Li, s.th. D- Lj is minimal;
(4) else f
(5) // use the routing table
(6) Let l=shl(D,A)
SUBROUTINES
I)Find_Another_Relay(S(rj),rj, Cmin):
7.For every “unmarked” relay rk with CR(S(rj),rk)>Cmin,do the following in the non-increasing order of CR(S(rj),rk).*
8.RunCheck_Relay_Availablity(rk,Cmin).
9.Ifrk is available , then do the following:
10.Remove relay node rj’sassigment to S(rj);
11.Assign relay node rk to S(rj).
12.Otherwise,continue on to next rk and go to line 8.
13.If all relays are unavailable,then S(rj) cannot find another relay.
II)Check_Relay_Availablity(rj,cmin):
14.Ifrj is not assigned to any source node,thenrj is available.
15.Ifrj=R(sb) or rj=0,then rj is available.
16.Otherwise,
17.Setrj as “marked”.
18.RunFind_Another_Relay(S(rj), rj,Cmin).
19.If S(rj) can find another relay,thenrj is available.
20.Otherwiserj is unavailable.
Assuming 16 bit NodeId, b = 2, number are expressed in base 2b = 4.
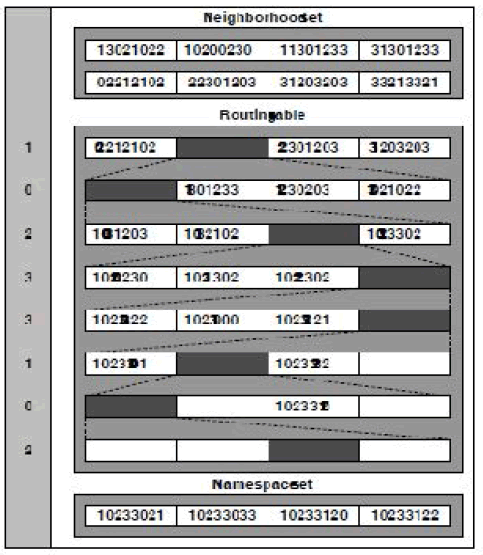
The Neighbourhood set, Routing table and Namespace set are clearly shown. In first diagram, x axis indicatesSize of candidate set B, and y axis indicates Algorithm results in milli seconds. Results of various algorithms are shown. In second diagram, x axis indicates Size of candidate set B and y axis indicates Time costs(s). In third diagram, x axis indicates Number of overlay node K and y axis indicates Algorithm Results in milli seconds. In fourth diagram x axis indicates Number of overlay node K and y axis indicates Time costs(s).
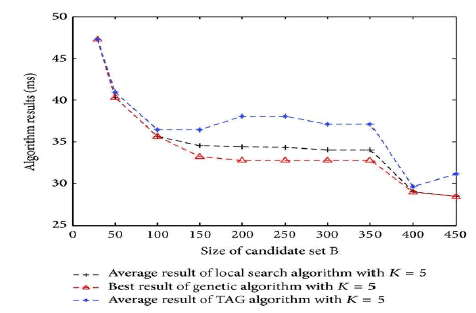
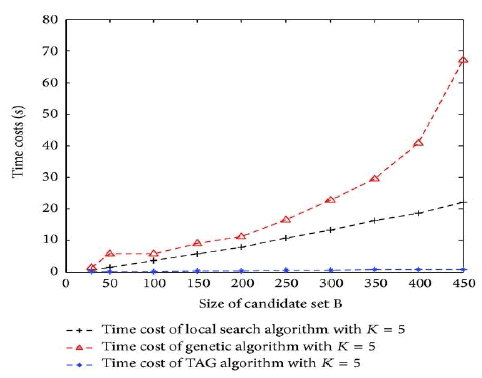
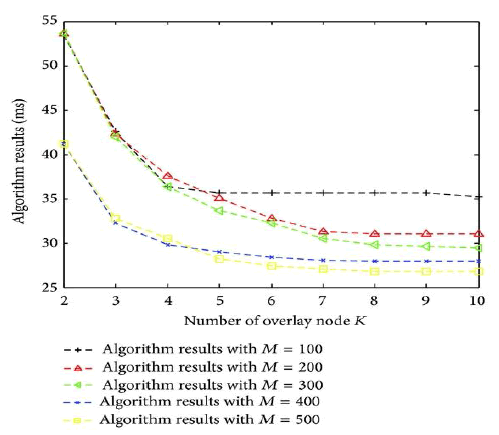
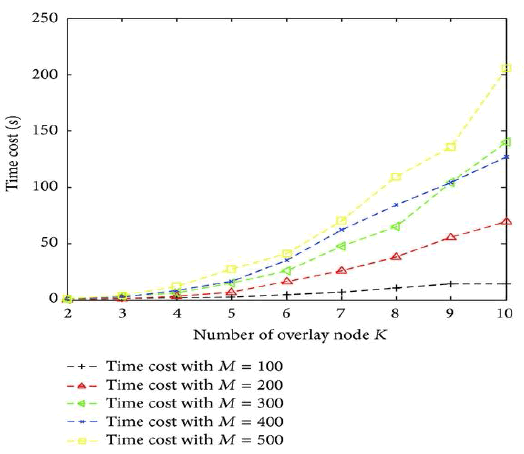
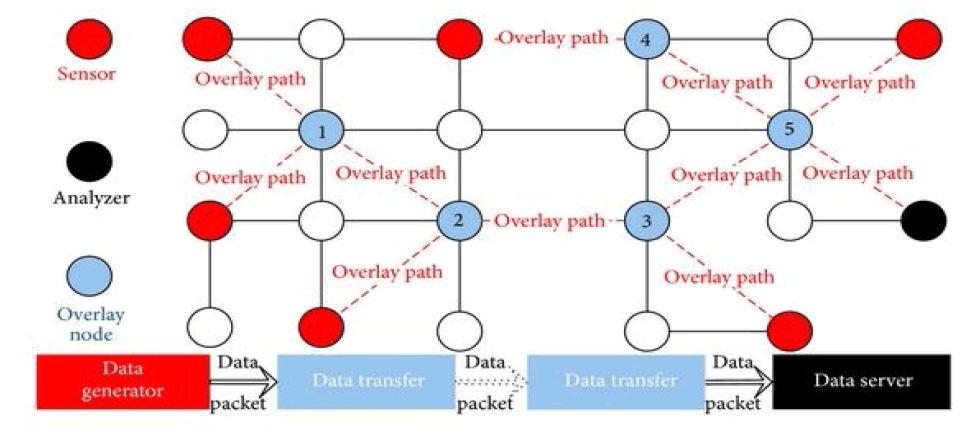
The main aim is to reduce the end-to-end delay and to achieve high reliability with fault tolerant between the sender and receiver and to make it cost effective. While using the PASTRY distributed routing algorithm and overlie routing to improve network performance was studied in the past by many works both practical and theoretical, very few of them consider the cost associated with the deployment of overlie infrastructure. The connection between the cost in terms of establishing overlie nodes and the benefit in terms of performance gain achieved due to the improved routing is not trivial, and it is interesting to investigate.
Mrs.Dr.A.Joshi has more than 13 years of experience in teaching and research ,completed, UG-B.Sc Mathematics-HolyCross College Trichy ,PG-M.Sc Mathematics-Nirmala College for Women Coimbatore, PhD Mother Teresa Women's university ME Sathyabama university
Mrs.D.Murugeswari has 8 years of teaching experience ,completed UG-B.Tech Information Technology in Sri Ram Engineering College ,Affiliated By Anna University,PG-M.Tech Computer Science and Engineering in Bharath University,Chennai