International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Responsive Communication Jamming Detector with Noise Power Fluctuation using Cognitive Radio

Mohsen M. Tanatwy
Associate Professor, Dept. of Network., National Telecommunication Institute, Cairo, Egypt
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

In this paper, we study detectors that can be potentially used to discover the radio signals that control the roadside bombs. The most important issue in this paper is that the study takes into consideration the noise power fluctuation with relatively variable signal to noise ratio. We examine two types of detectors in this paper the energy detection and matched filter and this paper propose a modified number of samples to detect the wireless controlled roadside bombs.

Keywords
Cognitive Radio; Responsive Communication Jamming; Noise Power Fluctuation

INTRODUCTION
Cognitive radio networks (CR) are one of the enabling technologies for future communication and networking [1]. CR networks have been developed for improving and optimizing the radio electromagnetic spectrum, by combining two main characteristics: cognitive capabilities and reconfigurability. The former is achieved by combining radio-scene analysis and predictive channel-state estimation, while the latter is provided by a platform known as software-defined radio upon which a cognitive radio is built on [2].
Devices used in roadside improvised explosive have become one of the most important threats in today’s asymmetric warfare and terrorist activities. These devices are inexpensive, easy to build or acquire, and difficult to trace and can be triggered from any detonation or exposure to targeted military forces. In many cases these device contain explosive material that is integrated with handheld wireless radio or device that will trigger upon receipt of a signal from a second wireless handheld device [3].
Vehicle-mounted barrage jammers have been in operation for some time [4]. These jamming systems continuously jam relevant frequency bands as a precaution against these wireless-enabled bombs irrespective of actual signal activities [5].

RELATED WORK
The concept of responsive communication jamming has been proposed to deal with the roadside improvised explosive devices. Responsive jamming is related to cognitive radio behaviour. The responsive jammer attempts to sense the bomb control signals and react by jamming it [6]. It is very important to both cognitive radio and responsive communication jamming is to get fast and reliable spectrum sensing. As the responsive communication jamming system is responsive for human lives we want the probability of missed detection to be as small as possible.
In this paper we will investigate the number of samples that are necessary to reach a given probability of missed detection and probability of false alarm with varying noise power level. The detectors considered are energy detector, and matched filter.
Most detection especially energy detectors are based on constant noise power [7-9], also same papers research on nonconstant noise power [10-15] while the number of samples calculated in [16] is 338 for energy detection and 91 for matched filter.

PROPOSED ALGORITHM
The problem of signal detection in additive Gaussian noise can be formulated as a binary hypothesis testing problem with the following hypotheses:
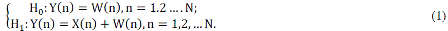image
Where Y(n), X(n) and W(n) are the received signals at CR nodes, transmitted signals at primary nodes and white noise samples, respectively; H1 and H0 stand for the decision that the licensed user is present or not, respectively. Noise samples W(n) are from additive white Gaussian noise process with power spectral density σ2 , i.e. W(n) �� N (0, σ2) [9].

Energy Detector
The performance of matched filter would serve the limit of possibility [17].
image
Under both hypotheses the test statistic is normally distributed. The probability of false alarm is
image
Where Q(·) is the standard Gaussian complementary cumulative distribution function (CDF) and P = Σ |X(n)|2/N is the average signal power, σ2 is the noise variance.
And the probability of detection is
image
To simplify the problem, energy detection algorithm based on average noise power without uncertainty has been discussed. United (3) and (4) eliminate the variable of decision threshold γ, and we can get:
image
Where Q−1 is the inverse standard Gaussian complementary cumulative distribution function (CDF), SNR = P/ σ2 is the signal-to-noise ratio.
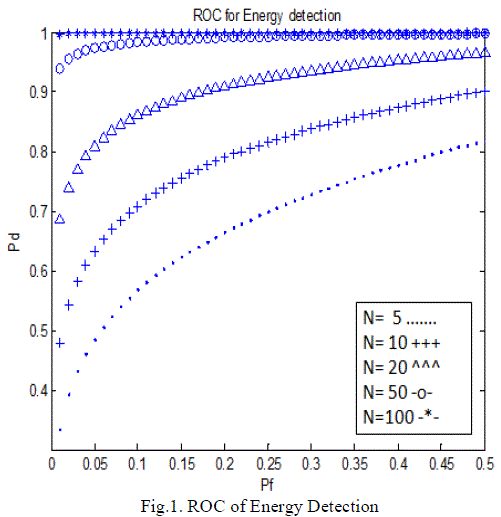
Figure 1 is the numerical results of equation (5), the simulation parameters are: SNR= 0 dB, pf (0, 0.5), and N ∈ {5, 10, 20, 50, 100}.
Figure 1 and the previous equations considered only the case without noise uncertainty. Now, consider the case with uncertainty in the noise model. The variance of noise with uncertainty can be included in a signal interval σ2n ∈ [ σ2n /β, βσ2n ]. Where β ≥ 1 is the noise fluctuation factor.
Equation (3) and (4) will be
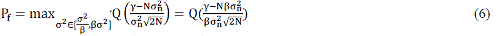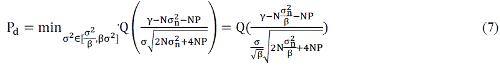image
image
Equations (6) and (7) show that if β=1 then the equations will tend to equation (3) and (4), If β increased with low SNR the required number of samples to get the same Pd and Pf must be increased. Also the previous equations show that if we assume 10-6 probability of false detection and 10-6 probability of missed detection (pmd = 1 − pd ) i.e., 0.999999 detection probability, then we need N=338 without considering noise fluctuation and this value increased to 344 with noise uncertainty of 1.05, and 415 for noise uncertainty of 1.1.
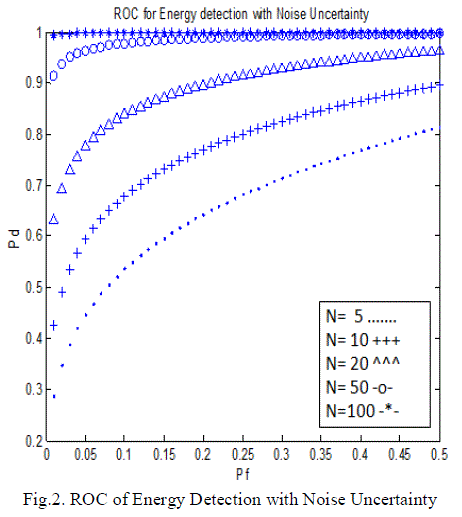
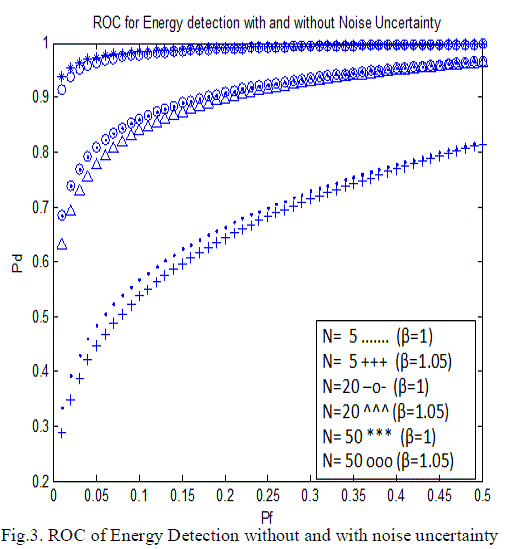
Figure 2 shows the receiver operating characteristics for energy detection with noise uncertainty β=1.05. And figure 3 compare between the ROC of energy detection without and with noise uncertainty for N=5, 20 and N=50. The figure shows that noise power uncertainty has a passive impact on the ROC especially with the small number of samples N.
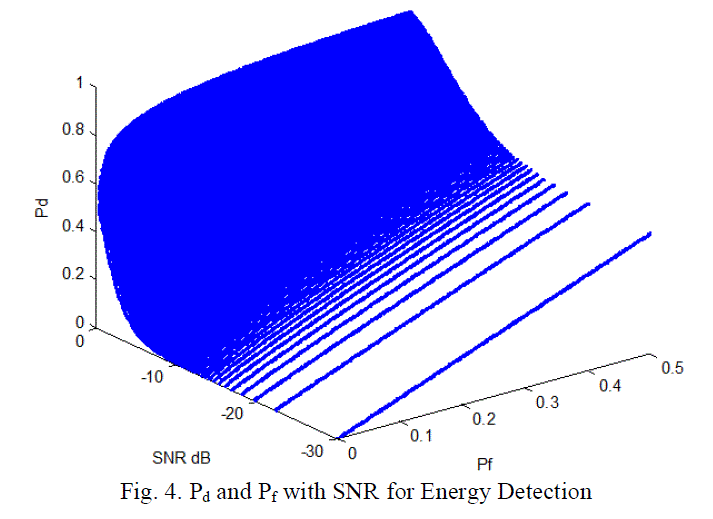
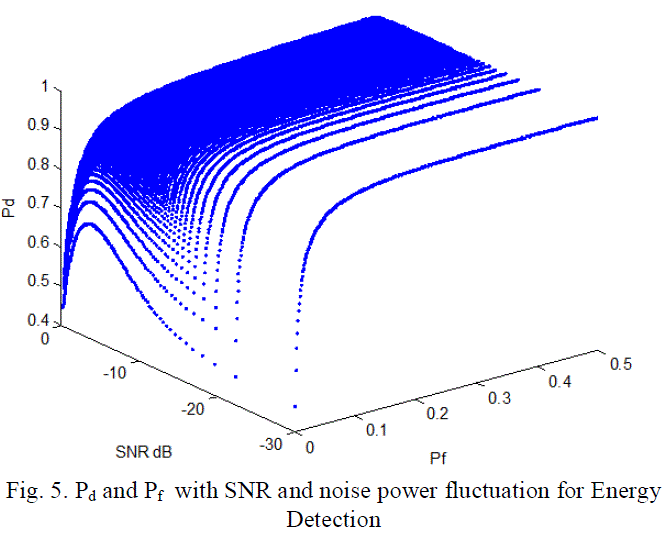
Figures 4 and 5 are the numerical results of equations (5), (6) and (7), the simulation parameters are: SNR∈ (0 dB, - 30dB), Pf ∈ (0, 0.5), and N = 20, and β=1.05. While figure 4 shows the effect of SNR on Pd and Pf for energy detection system, figure 5 shows the effect of noise power fluctuation with different SNR and their effect on both of Pd and Pf. Figure 5 shows that decreasing SNR or increasing the noise fluctuation factor will decrease the probability of detection specially for communication jamming detector that required small number of samples to be able to get fast detection.

Matched Filter
The matched filter is optimal detector of signals in white Gaussian noise. The drawback being that the detector needs a large amount of information about the signal it attempts to detect. Most likely we do not have all this information; however, the performance of matched filter would serve the limit of possibility.
image
Under both hypotheses the test statistic is normally distributed. The probability of false alarm is
image
And the probability of detection is
image
To simplify the problem, matched filter detection algorithm based on average noise power without uncertainty has been discussed. United (9) and (10) eliminate the variable of decision threshold γ, and we can get:
image
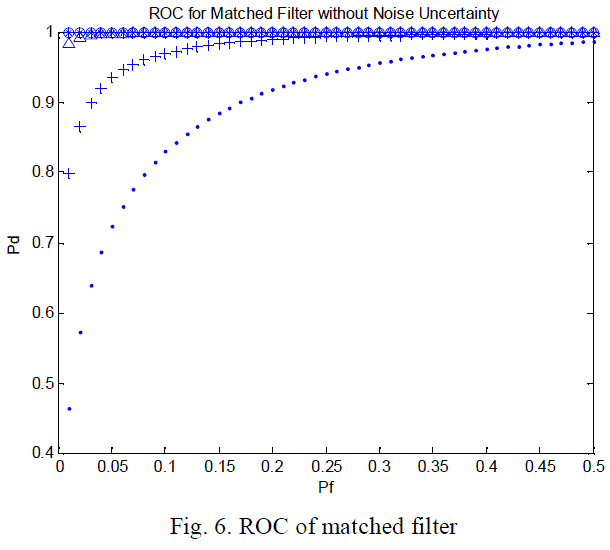
ROC for matched filter is shown in Figure 3 with the following numerical values: SNR=0 dB, false alarm probability Pf ∈ (0, 0.5).
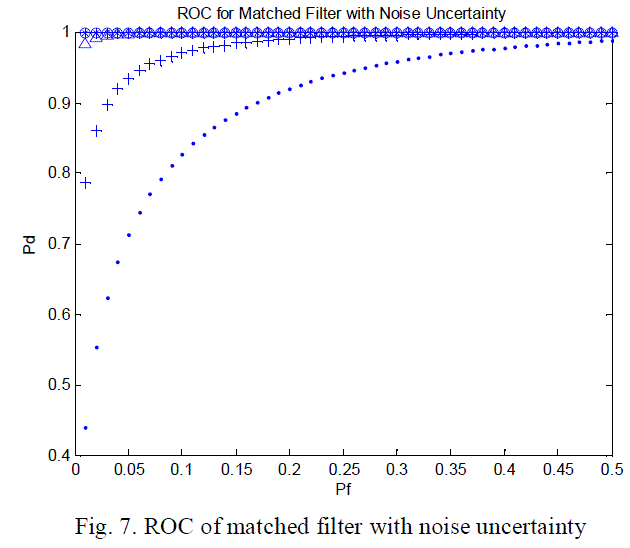
Figure 6 and equations (9), (10), and (11) considered only the case without noise uncertainty for matched filter. Now, consider the case with uncertainty in the noise model, equations (9) and (10) will be
image
image
Eliminating γ we can get
image
Equation (14) shows that if β=1 then the equation will tend to equation (11) and if β increased it slightly effect the required number of samples. Moreover equation (14) shows that if the probability of false detection is 10-6 and 10-6 probability of missed detection, then we need N=91 without considering noise fluctuation and this value increased to 95 with noise uncertainty of 1.5.
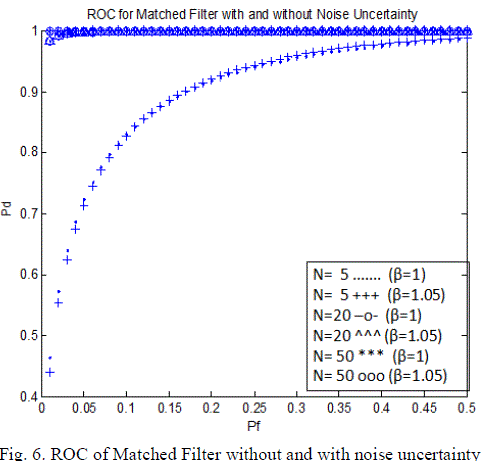
Figure 8 is the numerical result of equation (14), the simulation parameters are: Pf ∈ (0, 0.5), β=1.05 and N ∈ {5, 10, 20, 50, 100}. The figure shows that noise uncertainty has a small effect on the required number of detection sample. Comparing figures 1, 2, 6, and 7 show that the effect of noise uncertainty has much more effect in energy detection and can decrease the detection probability on the same number of detection samples.
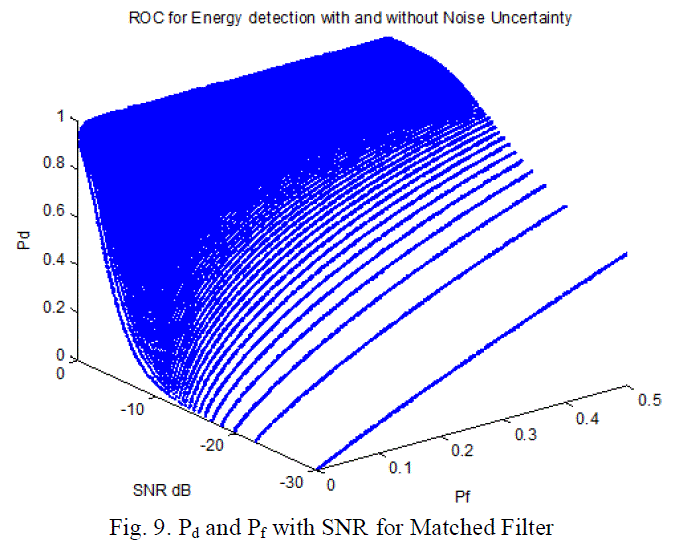
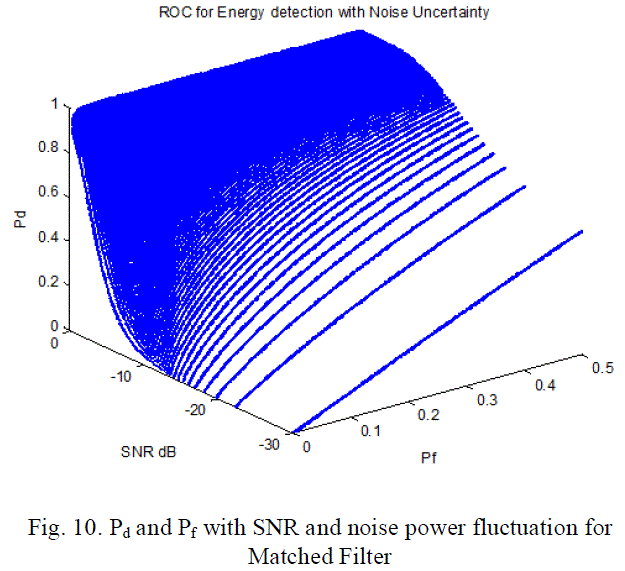
Figures 9 and 10 are the numerical results of equations (11) and (14), the simulation parameters are: SNR∈ (0 dB, - 30dB), Pf ∈ (0, 0.5), and N = 20, and β=1.05. While figure 9 shows the effect of SNR on Pd and Pf for matched filter, figure 10 shows the effect of noise power fluctuation with different SNR and their effect on both of Pd and Pf.

CONCLUSION AND FUTURE WORK
The results illustrate that energy detector is very sensitive to noise fluctuation and the minimum number of samples required to get certain missed probability increased with small fluctuation in noise. Meanwhile matched filter required sever fluctuation in noise to affect the required number of samples.
Previous works showed that the ideal number of samples for energy detector to get 10-6 missed probability is 338 and this work recommends 415 samples to avoid 10% noise fluctuation effect. This values is 91 sample for matched filter increased to 95 with 1.5 noise fluctuation factor.
This paper has verified that the performance decreased under noise uncertainty environments. This show that the choice of a fixed sample number is no longer valid under noise uncertainty and this should be chosen flexible as necessary. This work can be extended to Feature detector and Eigenvalue detector.
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 6 Figure 7 Figure 8 Figure 9 Figure 10
Figure 6 Figure 7 Figure 8 Figure 9 Figure 10
 

References