Keywords
|
| Cryptography, Data Hiding, Steganography, Watermarking. |
INTRODUCTION
|
| Digital steganography and watermarking are the two kinds of data hiding technology to provide hidden communication and authentication. The word steganography is derived from the Greek words “stegos” meaning “cover” and “grafia” meaning “writing” [3] defining it as “covered writing”. In contrast to Cryptography, where the enemy is allowed to detect, intercept and modify messages without being able to violate certain security premises, the goal of steganography is to hide a secret message inside harmless medium in such a way that it is not possible even to detect that there is a secret message. The medium for data hiding is also called as cover, host and carrier. |
| To human eyes, data usually contains known forms, like images, videos, sounds and text. Most internet data naturally includes unwarranted headers too. These are media exploited using steganograpy techniques. Images are the most powerful medium for data hiding because of the limitation of Human visual System(HVS). Basic idea of watermarking is to embed covert information into a digital signal, like digital audio, image, or video, to trace ownership or protect privacy. Data hiding can be used in a large amount of data formats in the digital world of today. The most popular data formats used are .bmp, .doc, .gif, .jpeg, .mp3, .txt and .wav mainly because of their popularity on the Internet. |
| An information-hiding system is characterized using four different aspects: capacity, security, perceptibility and robustness[2] shown in Fig. 1. |
| • Capacity refers to the amount of information that can be hidden in the cover medium. |
| • Security refers the inability of the hacker to extract hidden information. |
| • Perceptibility means the inability to detect the hidden information. |
| • Robustness is the amount of modification the stego-medium can withstand before an adversary can destroy the hidden information. |
REVERSIBLE DATA HIDING
|
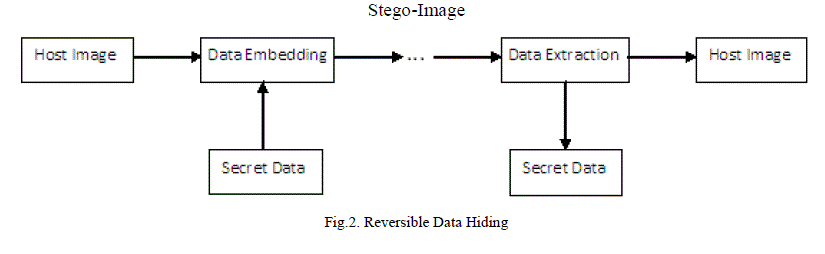
| The data embedding process will usually introduce permanent loss to the cover medium. However in some applications such as medical, military, and law forensics degradation of cover is not allowed. In these cases, a special kind of data hiding method called reversible data hiding or lossless data hiding is used. Reversible Data Hiding (RDH) in digital images is a technique that embeds data in digital images by altering the pixel values for secret communication and the cover image can be recovered to its original state after the extraction of the secret data. The block diagram of RDH is shown in Fig.2. Reversible steganography or watermarking can restore the original carrier without any distortion or with ignorable distortion after the extraction of hidden data. So reversible data hiding is now getting popular. In this paper some important reversible data hiding techniques for digital images are explained and the results are analyzed. |
RDH TECHNIQUES
|
| A considerable amount of research on reversible data hiding has been done over the past few years. Four important techniques are discussed here. |
Integer Transform Technique
|
| In this scheme, an integer transform is used to embed 1-bit watermark into one pixel pair in a way that the sum of the pixel pair remains unchanged. Based on the invariability of sum values and the equality between the parities of sum values and difference values, the extraction of watermarks and the recovery of pixel pairs can be easily achieved. |
| Shaowei Weng et al.[14] proposed an integer transform in which the forward transform is defined as |
 |
| where b is used to denote one bit watermark, and d is the difference between the pixels x and y. Actually, x + y equals x’ + y’. x + y and d have the same parity. x’ and y’ are the watermarked image pixels corresponding to x and y. |
| On the decoding side, the sum of x’ and y’ is calculated first. Therefore x + y are determined. The difference value of x’ and y’ is calculated and denoted as d’. The actual difference d can be calculated as |
 |
| The value of d and the watermark bit b can be uniquely deduced because the parity of d is known and b is a binary number. For example, if x = 7, y = 5 and b = 0, then x’ = 8, y’=4 after embedding. On the receiver side, (d’ + LSB(d’))/2 is calculated as 2. The parity of d can be guaranteed to be the same as d’. The parity of d’ is odd parity. The parity of d is odd if and only if b = 0. As a result, watermark bit b is correctly extracted and the value of d is obtained. Once d and x + y are obtained then the original pixel values x and y are calculated as |
 |
Difference Expansion Technique
|
| Yongjian Hu [19] uses the predicted image pixel error instead of the pixel-pair difference for Difference Expansion(DE) embedding. A predictor below can exploit the neighboring information to predict an image pixel. |
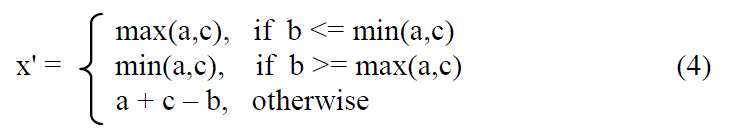 |
| where x’ represents the predicted pixel value corresponds to pixel value x. a, c and b are right, lower, and diagonal neighbors of x. One information bit is embedded into a predicted error e = x – x’. To ensure lossless recovery of the original image, embed information bits into predicted errors that do not cause the overflow/underflow of image gray levels. In other words, predicted error does not exceed the integer range [0,255] for an 8-bit image. |
| In the embedding scheme, divide the histogram of predicted errors into two parts: the inner region for embedding and the outer regions for shifting. Assume that two thresholds, Tr and Tl, are used to control the right and left boundaries of the inner region, respectively. So the inner region is represented as [-Tl ,Tr-1], and the corresponding outer regions are [-Pel , -Tl-1] and [Tr , Per]. Here Pel and Per refer to the left and right ends of the histogram. The whole embedding process includes two manipulations. First, the outer region has to be shifted before embedding. The shifted pixel value x’’ is |
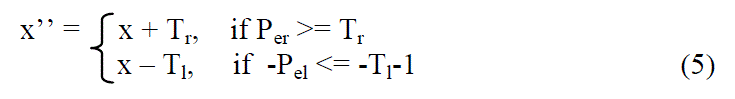 |
| Then, in the inner region, secret bit b is embedded by DE embedding as |
| x'’ = x + Pe + b , if -Tl <= Pe <= Tr-1 (6) |
| The recovery process also includes two manipulations. In the inner/embedded region, the embedded/hidden bit is extracted. In the shifted regions, the original pixel value is resumed. For difference expansion based reversible data hiding, the embedded bit-stream mainly consists of two parts: one part that conveys the secret message and the other part that contains the binary (overflow) location map and the header file. The first part is the payload while the second part is the auxiliary information package for blind detection. To increase embedding capacity, we have to make the size of the second part as small as possible. The compressibility of location map has to be increased for different types of images. |
Histogram Modification Technique
|
| In histogram modification technique [17], the differences between adjacent pixels instead of simple pixel value is considered. Since image neighbor pixels are strongly correlated, the difference is expected to be very close to zero. |
| At the sending side, first scan the image in an inverse s-order and calculate the pixel difference di between pixels xi-1 and xi by |
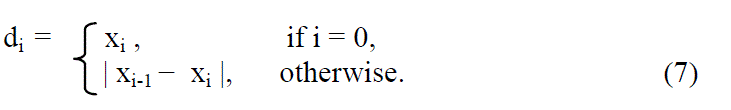 |
| Determine the peak point P from the histogram of pixel differences. Then again scan the whole image in the same inverse s-order and if di > P, shift xi by 1 unit as follow |
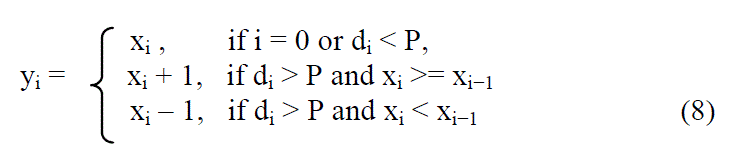 |
| where yi is the watermarked value of pixel i. If di = P, modify xi according to the message bit b as follow |
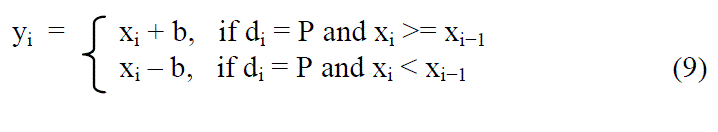 |
| At the receiving end, the recipient extracts message bits from the watermarked image by scanning the image in the same order as during the embedding. The message bit b can be extracted by |
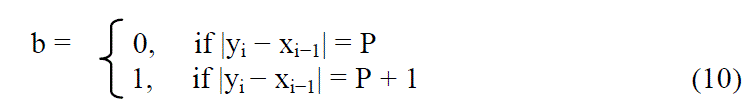 |
| where xi−1 denotes the restored value of yi−1. The original pixel value can be restored by |
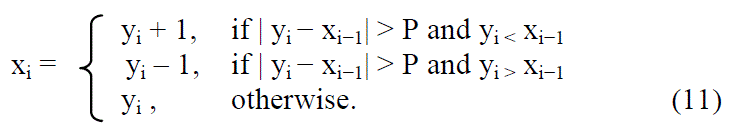 |
| Thus, an exact copy of the original host image is obtained. These steps complete the data hiding and extraction process in which only one peak point is used. Large hiding capacities can be obtained by repeating the data hiding process. However, recipients may not be able to retrieve both the embedded message and the original host image without knowledge of the peak points of every hiding pass. A binary tree structure used to deal with communication of multiple peak points. Modification of a pixel may not be allowed if the pixel is saturated (0 or 255). To prevent overflow and underflow, histogram shifting technique is used that narrows the histogram from both sides. |
Interpolation Technique
|
| In this technique [10], the difference between interpolation value and corresponding pixel value is used to embed bit “1” or “0” by expanding it additively or leaving it unchanged. It is different from most differential expansion approaches in two important aspects: |
| 1) It uses interpolation-error, instead of interpixel difference or prediction- error, to embed data. |
| 2) It expands difference, which is interpolation-error here, by addition instead of bit-shifting. |
| First, interpolation values of pixels are calculated using interpolation technique, which works by guessing a pixel value from its surrounding pixels. Then interpolation-errors are obtained by |
 |
| where x’ are the interpolation values of pixels x. The secret bit b is embedded by additively expanding the interpolation error values. The additive interpolation-error expansion is formulated as |
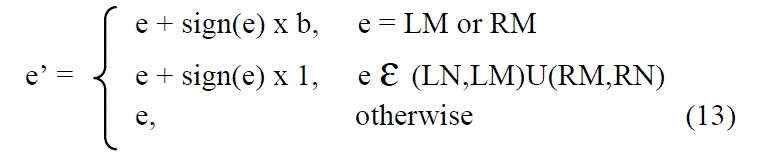 |
| where LM and RM denote the corresponding values of the two highest points of interpolation-errors histogram and LN and RN denote the corresponding values of the two lowest points of interpolation-errors histogram. The watermarked pixels x’’ becomes |
 |
| During the extracting process, the interpolation value x’ is computed with the same interpolation algorithm and the corresponding interpolation-errors are obtained. Once the interpolation errors, LM, RM, LN and RN are known, the embedded secret data can be extracted. Then the inverse function of additive interpolation-error expansion is applied to recover the original interpolation-errors. Finally, we can restore the original pixels x by adding interpolation value x’ and the interpolation error e. |
| After secret messages are embedded, some overhead information is needed to extract the covert information and restore the original image. The overhead information are the information to identify those pixels containing embedded bit(LM,LN,RM and RN) and the information to solve the overflow/underflow problem. |
RESULTS AND DISCUSSION
|
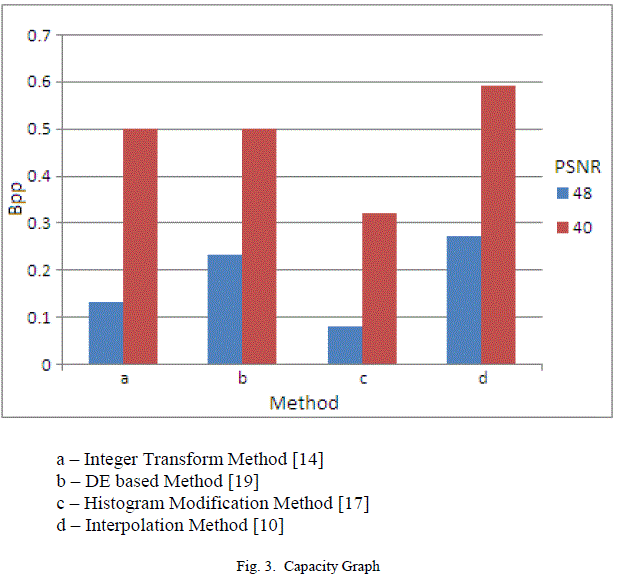
| The four different techniques explained in the above section was tested on several gray-level and color images. Results obtained for the classical 512 x 512 Lena image is shown here. Total number of pixels in that image is 262144. Peak Signal to Noise Ratio (PSNR) value and BPP(Bits Per Pixel) value are used as quality measures. The hiding capacity of different techniques for PSNR value nearly 40 and 48 are shown in Table 1. The hiding capacity of interpolation method is higher when comparing with other techniques. Integer transform method and Difference expansion based method have the hiding capacity near to 0.5 bpp when PSNR value is near to 40. Histogram modification method has low hiding capacity. Integer transform method, DE based method and Interpolation method crosses the standard capacity mark 0.5 bpp when PSNR Value is near to 40. These results are also shown as graph in Fig.3. |
CONCLUSION
|
| Reversible data hiding techniques getting popular because of the reversibility of carrier medium in the receiving end after extraction of secret data. In this paper four different types of reversible data hiding techniques for digital images: Integer transform technique, Difference expansion technique, Histogram modification technique and Interpolation technique are studied, analyzed and compared. The survey results show each technique has its own advantage and disadvantages. |
| |
Tables at a glance
|
 |
| Table 1 |
|
| |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
| |
References
|
- Abbas Cheddad, Joan Condell, KevinCurran and Paul Mc Kevitt, (2010), “Digital Image Steganography: Survey and Analysis of Current Methods”, Elsevier signal processing, Vol. 90, pp. 727-752.
- Ali Al-Ataby and Fawzi Al-Naima,(2010), “ A Modified High Capacity Image Steganography Technique Based on Wavelet Transform”, The International Arab Journal of Information Technology, Vol. 7, No. 4, pp 357-363.
- Bret Dunba r,(2002), “A detailed look at stegonagraphic Techniques and their use in an Open – Systems Environment”, SANS Institute.
- Chang C.C, Lin C.C and Chen Y.H,(2008), “ Reversible Data Embedding Scheme using Differences Between Original and Predicted Pixel values” , IET Information Security, Vol. 2, No. 2, pp. 35–46.
- Chin-Chen Chang, Wei-Liang Tai, and Chia-Chen Lin,(2006), “A Reversible Data Hiding Scheme Based on Side Match Vector Quantization”, IEEE Transaction on Circuits and Systems for Video Technology, Vol.16, No. 10, pp 1301-1308.
- Coltuc D and Tremeau A,(2005), “ Simple Reversible Watermarking Schemes ”, Proc. of SPIE, Security, Steganography, Watermarking of MultimediaContents, Vol. 5681, pp. 561–568.
- Dalel Bouslimi, Gouenou Coatrieux, Michel Cozic and Christian Roux,(2012), “ A Joint Encryption/Watermarking System for Verifying the Reliability of Medical Images”, IEEE Transactions on Information Technology in Biomedicine, Vol. 16, No.5, pp. 891- 899.
- J. Fridrich, D. Soukal, (2006), “Matrix Embedding for Large Payloads”, IEEE Transactions on Information Forensic and Security, Vol.1, No.3, pp. 390-395.
- Jennifer L. Wong, Gang Qu and Miodrag Potkonjak,(2004), “Optimization-Intensive Watermarking Techniques for Decision Problems” , IEEE Transaction on Computer- Aided Design of Integrated Circuits and Systems, Vol. 23, No. 1, pp. 119-127.
- Lixin Luo, Zhenyong Chen, Ming Chen, Xiao Zeng and Zhang Xiong, (2010), “Reversible Image Watermarking Using Interpolation Technique ” , IEEE Transaction on Information Forensics and Security, Vol. 5, No. 1, pp 187 – 193.
- A.Nag, S. Biswas, D. Sarkar, P.P. Sarkar ,(2010), “A Novel Technique for Image Steganography Based on Block-DCT and Huffman Encoding”, International Journal of Computer Science and Information Technology, Vol. 2, N0. 3, pp. 103-112.
- Neminath Hubballi and Kanyakumari D P,(2009), “Novel DCT based watermarking scheme for digital images”, International Journal of Recent Trends in Engineering, Vol. 1, No. 1, pp. 430-43.
- Niels Provos and Peter Honeyman,(2003), “Hide and Seek: An Introduction to Steganography” , IEEE Security & Privacy, pp.32-44.
- Shaowei Weng, Yao Zhao, Jeng-Shyang Pan and Rongrong Ni,(2008), “Reversible Watermarking Based on Invariability and Adjustment on Pixel Pairs”, IEEE signal processing letters, Vol. 15, pp. 721-724.
- Tsz Kin Tsui, Xiao-Ping Zhang Androutsos, (2008), “Color Image Watermarking Using Multidimensional Fourier Transforms” , IEEE Transactions on Information Forensics and security, Vol. 3, pp.16-28.
- Vaishali S. Jabade and Dr. Sachin R. Gengaje, (2011), “Literature Review of Wavelet Based Digital Image Watermarking Techniques”, International Journal of Computer Applications, Vol 31, No.1, pp. 28-35.
- Wei-Liang Tai, Chia-Ming Yeh and Chin-Chen Chang,(2009), “Reversible Data Hiding Based on Histogram Modification of Pixel Differences”, IEEE Transaction on circuits and systems for video technology, Vol. 19, No. 6, pp. 906-910.
- Weiming Zhang, Biao Chen and Nenghai Yu,(2012), “Improving Various Reversible Data hiding Schemes Via Optimal Codes for Binary Covers”, IEEE Transactions on Image Processing, Vol. 21, No. 6, pp. 2991-3003.
- Yongjian Hu, Heung-Kyu Lee and Jianwei Li,(2009), “DE- Based Reversible Data Hiding With Improved Overflow Location Map”, IEEE Transaction on Circuits and systems for video technology, Vol. 19, No. 2, pp. 250-260.
|