ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Swati Chowdhary1, Prof.Mamta M Sarde2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
The basic problem is to identify the means to achieve accurate coefficient and then to select the objective required in efficient manner and for this optimization is the best technique which is defined as selection of a best element from some set of available alternatives. An optimization problem consists of maximizing or minimizing a real function by systematically choosing input values from within an allowed set and computing the value of the function. In this paper there is a study of different algorithms and their classification used in digital filter design to get the coefficient accurate.
Keywords |
| Optimization, Simulated Annealing Algorithm, Differential Evolution Algorithm, Genetic Algorithm |
INTRODUCTION |
| Optimization is simply choosing a design parameters to improve some objective. It is extracting some model parameters from data while minimizing some error measure. An optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete variables is known as a combinatorial optimization problem. In a combinatorial optimization problem, we are looking for an object such as an integer, permutation or graph from a finite (or possibly countable infinite) set. |
| The standard form of a (continuous) optimization problem is |
| Minimize f(x) |
| subject to g i(x) ≤ 0, i=1,….,m (1) |
| Hi(x)=0, i=1,….,p (2) |
| where |
| f(x): R n→ R is the objective function to be minimized over the variable x, |
| g i (x) ≤ 0 are called inequality constraints, and |
| hi(x) = 0 are called equality constraints. |
| By convention, the standard form defines a minimization problem. A maximization problem can be treated by negating the objective function |
| Formally, a combinatorial optimization problem A is a quadruple (I, f, g, m), where given an instance x and a feasible solution y of x, m (x, y) denotes measure of y which is usually a positive real. |
| I is a set of instances, is the goal function, and is either min or max. |
| The goal is then to find for some instance x an optimal solution, that is, a feasible solution y with |
| m(x, y)=g{m( x, y‘)|yâÃâ¬ÃŸ∈ f(x)} (3) |
| For each combinatorial optimization problem, there is a corresponding decision problem that whether there is a solution for some particular measure m0. Hence optimization problem is based on computational time which is required to solve the problem .The classification of optimization is in next section. |
A. Classification of Optimization Problem: |
i)Classification of continuous optimization problems: |
| Optimization problems are classified as either convex or non-convex based on whether the domain and the cost function are both convex or not. The domain is convex if a straight line between any two points s1 and s2 in the domain is also part of the domain, and the cost function is convex if its value at any point along the straight line between any two points s1 and s2 in the domain has an upper bound in the chord through (s1; f(s1)) and (s2; f(s2)). |
ii)Classification of combinatorial optimization problems: |
| The classification of combinatorial optimization problems, which is completely different from that of continuous problems, is based on the computational time needed to solve problems as the size grows. A distinction is made between problems which has a solution time, with respect to the best known algorithm, that is a polynomial function of the problem size and those which require a super polynomial, e.g. any function that grows faster than a polynomial, execution time in terms of their size. [1] |
OPTIMIZATION ALGORITHMS |
| An optimization algorithm is related to the particular optimization problem at hand, but in general this algorithms applicable only to a subset of a problem to general algorithms tackling many problems without modification. The general algorithm is time computing time while an efficient general algorithm “fast enough" is in most cases. There are some algorithms which are used to compare complexity and executing time required are elaborated below. |
B.Simulated Annealing (SA) algorithm: |
| The simulated annealing (SA) optimization algorithm is based on an analogy between the behaviors of a melted solid that is slowly cooled (annealed) into a “perfect" crystal. The algorithm, together with genetic and neural network algorithms, belongs to a group of algorithms sometimes referred to as “natural" algorithms since they rely on observations made in the study of natural systems such as the forming of crystals, the evolution of the species, and the workings of the human brain.[1] |
| The key algorithmic feature of simulated annealing is that it provides a means to escape local optima by allowing hillclimbing moves (i.e., moves which worsen the objective function value). As the temperature parameter is decreased to zero, hill climbing moves occur less frequently, and the solution distribution associated with the in homogeneous Markov chain that models the behavior of the algorithm converges to a form in which all the probability is concentrated on the set of globally optimal solutions [2] |
C.FIR filter design with simulated annealing algorithm: |
| Boltzmann annealing (Ingber, 1989), which is defined by the following elements: |
| Where g (b n) is the probability density function (p d Sf) of the filter coefficients b n deviation, Δ b n=b n (t+1) – b n is the deviation from state (filter) i to i +1, and T is a measure of the fluctuations of the Boltzmann distribution g in the N −1 h(b n ) = 1âÃËÃâ¢(1+e ΔEâÃËÃâ¢T ) where h(b n) is the (PDF) probability for acceptance of new between the present and the previous values of the cost-function [2] i.e. filter error T(k)=T 0 âÃËÃâ¢l n k–, where T(k) is the schedule of annealing the temperature T in annealing-time steps. Simulated annealing is beneficial with arbitrary systems and cost functions for any given problem as well as it statistically guarantees finding an optimal solution for any optimization problem, besides this if annealing with a (1/log k) is very time consuming for complex cost function makes major drawback of SA. [3] |
D. Differential Evolution(DE) Algorithm: |
| DE is very simple yet robust, powerful, stochastic, population based and easy to use optimization algorithm, which has been developed to optimize real parameter and real valued functions. The name of the algorithm is chosen as Differential Evolution (DE) to indicate a special type of differential operator in it that has been utilized to Create offspring from the parent chromosomes without adopting crossover or mutation. Differential Evolution algorithms can be divided into four steps, namely Initialization, Mutation, Recombination, and Selection. |
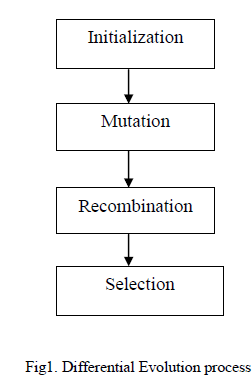 |
Initialization |
| To obtain better result choose a suitable range of value which specify the search variables to optimize this technique. Thus if the j th gene of each chromosome has its lower and upper bound as x j L and x j U respectively, then the corresponding gene of i th chromosome can be initialized as |
| where i= 1,2,3, … . . , P and rand (0, 1) is a uniformly generated random number in [0, 1]. |
Mutation |
| Initialization process only takes care of a entire search space. To find the optimum solution for a given problem there is a need to explore the entire search space which can be expanded in the process of mutation to generate a new population vector in which various parameter vectors are combined together. |
| DE technique is termed for different mutation strategies. |
| In DE/rand/1 scheme, donor vector of generation ‘G+1’ can be formed from the population vector of the generation ‘G’ as |
| V i(G+1)rand/1=X p 1(G)+F.[X P2 (G)-XP 3 (G)] (6) |
| F is called the weighting factor with i,p1,p2,p3ε P where P is the set of population members of the evolutionary computation. The parameter |
| F is responsible for the amplification of the differential variation and generally lies within the range [0, 2]. |
Recombination |
| This is the third step of DE, called cross-over or recombination. Recombination process plays an important role enhance the potential diversity of the population which is a scheme of crossover where donor vector exchanges its components. Two types of recombination exist in the literature, namely exponential and binomial cross-over. The trial vector |
 |
| where k=1,2, … . . , L and L is another integer from the interval [1, D]. The parameter L signifies the number of components contributed by the donor vector to the target vector. |
Selection |
| The final decision is taken at the last step of DE, called selection process. The present parameter vector passes through the next generation. This can well be described by means of the following equation |
| Where ℑ(Yi (G)) identifies the cost functional value resulting from the i th vector Υ i(G) at iteration ‘G’. [5] |
E. FIR filter design with Differential Evolution Algorithm: |
| For designing low pass FIR filter different mutation schemes are used. In optimization algorithm, the efficiency of DE is presented by a mathematical expression called the cost function. Here the fitness value and cost functional value may be regarded as two different functions of identical items as follows: |
 |
| The parameter ‘φ’ in and reflects the formulation of the error function and for the design of a low-pass filter with a cut-off frequency ω takes the form as shown in the following equation: |
| The other parameters within the parenthesis in symbolize the set of mutation strategy, recombination strategy and control parameter and has been outlined [5] as follows: |
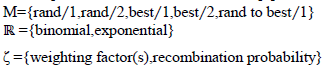 (13) (13) |
F. Genetic Algorithm |
| Genetic Algorithm (GA) are very flexible, non-problem specific, and robust.GA can explore multiple regions of the parameter space for solutions simultaneously. GA can discard suboptimal solutions in favour of more promising subsequent local solutions. They require a very large amount of computation. The GA consists four main stages: evaluation, selection, crossover and mutation. The evaluation procedure measures the fitness of each individual solution in the population and assigns to it a score. The selection procedure randomly selects individuals of the current population for development of the next generation. The crossover procedure takes two selected individuals and combines them about a crossover point thereby creating two new individuals. The mutation procedure randomly modifies the genes of an individual subject to a small mutation factor, introducing further randomness into the population. This process continues until one of the possible termination criteria is met: if a known optimal or acceptable solution level is attained; or if a maximum number of generations have been performed; or if a given number of generations without fitness improvement occur, (Goldberg 1989; Lewin 1994, 1996). |
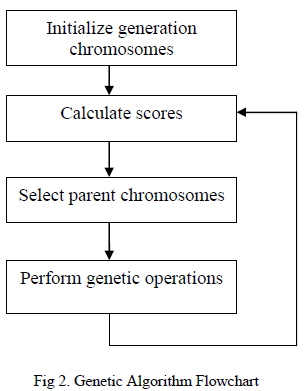 |
G. FIR filter design with Genetic algorithm: |
| Consider a linear phase FIR filter, we want to find an N tap FIR filter that will approximate the frequency response of the ideal low pass filter as shown in figure . The transfer function of an FIR filter of order N is: |
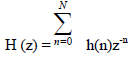 (14) (14) |
| The corresponding frequency response is given by: |
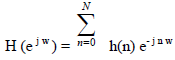 (15) (15) |
| In the case of linear phase, the transfer function will have symmetric coefficients that is h(n)=h(-n) an H(ejω)=H(w)ejφ(ω) where |
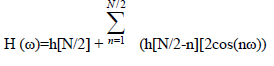 |
| Now we sample the frequency in [0,pi] with N points, |
| The error function (âÃâÃâ¡) now can be defined as |
| ∈ (ω)=[H d(ω)-H(ω)] (18) |
| And the fitness function that has been used is the inverse of the absolute value of the error function (H): |
| Fitness=1/abs(ε(ω)) (19) |
| Now the input to the GA will be as follow: Genetic Algorithm used to find the impulse response, and the matrix that will be [6] |
| x=[M ,h[n-1/2].h[n-1/2+1]……h[n-1]] (20) |
| M=N-1/2 |
CONCLUSION |
| In order to get the coefficient accurate in less computational time an improved algorithm that is integer linear programming involves reducing of number of ripples with the filter specification within pass band and stop band. This algorithm also offers a fast execution. It also involves minimizing of non zero bits to get accuracy in the coefficient in particular filter specifications. |
References |
|