Keywords
|
| Collaborative filtering, homomorphic encryption, privacy, recommender system. |
INTRODUCTION
|
| Now a day’s most of people are using online services for daily activities [1], which require sharing personal information with the service provider. Some examples are social networks and online shopping. |
| Social networks: In this, people share personal information like images and videos with other people. Service providers receive this data and forward to the third parties. A common service for providing recommendations is for finding friend, groups and events by using collaborative filtering and required data is collected from users. |
| Online shopping: In online shopping, providing various suggestions to the customers causes growth of e-business. From the user’s choices and clicks, suggestion of suitable products or services is provided to the customers [2]. |
| In this type of services, recommendation systems based on collaborative filtering techniques that collect and process user’s personal data [3]. From these online services people benefit but direct private data access by service provider has potential privacy risks for users since this data can be misused or leaked to other party [4]. These privacy considerations in online services seem to be one of the most important factors that can increase the growth of ebusiness [5]. Therefore privacy protection of users gives benefits to both individuals and business. |
| The techniques for generating recommendations for users strongly rely on the way personal user information is gathered. This information can be provided by the user himself as in profiles, or the service provider can observe users’ actions like click logs. On one hand, more user information helps the system to improve the accuracy of the recommendations. On the other hand, the personal information on the users creates a service privacy risk since there is no solid guarantee for the service provider not to misuse the users’ data. It is often seen that whenever a user enters the system, the service provider claims the rights of the information provided by the user and authorizes itself to distribute the data to third parties for its own benefits [5]. |
| The execution of this method mainly depends on the number of user’s participation in the calculation since for the system to work; the users need to be present in huge amount. This creates a trade-off between accuracy/correctness of the recommendations and number of users in the system. Also, the output of the algorithm is available to the server, which causes a privacy threat to the users. Therefore the randomization techniques are supposed to be highly insecure [6]. |
RELATED WORK
|
| Canny et al (2002) [7] present a method to protect the privacy of users based on analysis model by using a similar approach as in [8]. While Canny works with encrypted user data, Polat and Du imply to secure the privacy of users with the help of randomization techniques [9, 10]. |
| Polat et al (2003) [9] used (RP) randomized perturbation techniques. Some techniques allow users to hide their personal information without disclosing their identities but there is no guarantee on the quality of the data set, so it propose a new system in which user first hide his/her personal data and then sends to central place where as the data collector cannot derive the hidden information about users private data.Atallah et al (2004) [11] present privacypreserving collaborative forecasting and benchmarking to increase the reliability of local forecasts and data correlations using cryptographic techniques. |
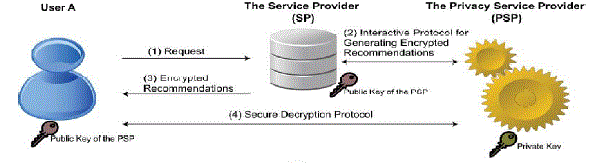
| Erkin et al. (2012) [2] also propose protocols based on cryptographic technique, which are computationally more efficient than their counter parts in [12], [13].The cryptographic protocol for generating recommendations to the users within online applications. To overcome this problem of active participation of user Erkin introduce homomorphic encryption schemes and secure multiparty computation (MPC) techniques for privacy enhanced recommender system by using a semi trusted third party i.e. Privacy Service Provider (PSP) who is trusted to perform the assigned tasks properly, without examining the user’s private data. By including this third party PSP, users upload their encrypted data to the service provider and by using collaborative filtering techniques between service provider and privacy service provider without interaction with the user the recommendations are generated. |
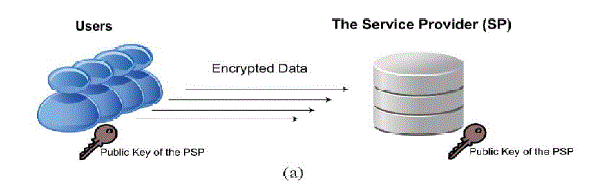
| As shown in fig.1.Erkin et al (2012) [2] proposes a protocol is to hide information that may damage privacy of users. Details about the user’s ratings, similarity value calculation to a threshold and generated recommendations are all kept hidden from SP, PSP and other users. First, the users hide their personal data by encryption and send it to the service provider. And to generate recommendations the service provider and the PSP run a cryptographic protocol without interacting with the users. For this intention Paillier system is used before. This cryptosystem is used to encrypt the privacy-sensitive data of the users. |
P. Paillier et al (1999) [14] introduces a scheme known as Paillier technique: The encryption of a message,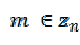 by using the Paillier technique is defined as- by using the Paillier technique is defined as- |
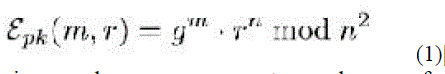 |
| Where n is a product of two large prime numbers p, q, g, generates a subgroup of order n, and r is a random number in Zn .The public key is (n, g) and the private key is (p ,q) . The homomorphic property of the Paillier cryptosystem can be easily verified as shown below: |
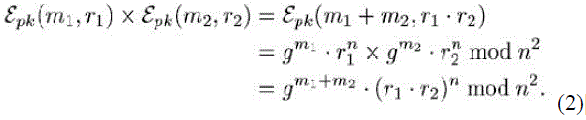 |
| The technique of collaborative filtering is used with the Paillier system which includes following 3 steps [3]: |
| 1) Compare similarities between a user and other users. |
| 2) The most similar users (L) are selected by comparing their similarity values with a threshold. |
| 3) By average rating of most similar users (L), the recommendations are generated. |
| To find similar users, A & B with vectors and where M number of items and small and positive integer. |
| Cosine similarity: |
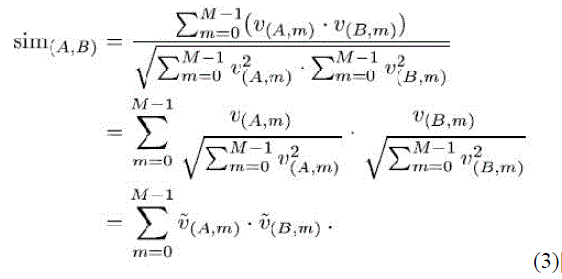 |
| After computing cosine similarity, the service provider compares similarity values with a threshold δ. The ratings of L users whose similarity to A exceeds δ are summed and divided by L. This result is presented as the recommendations. |
PROBLEMS AND DIRECTIONS
|
| There are some problems and concerns present in the current Paillier Cryptosystem which are examined in this unit. This unit also provides certain possible solutions to the problems in the existing techniques. In Paillier system user’s active participation is must, which makes the system very time consuming as well as complex. This is because user has to perform all encryptions and decryptions number of times, which makes the system costly. Also user interaction may harm the system’s security, which causes privacy of users. Again large data system becomes expensive, which makes the system less efficient [2], [7], and [8]. |
| To solve the above stated problems proper solution is required. Therefore work with RSA (Rivest, Adi Shamir and Leonard Adleman) and ElGamal algorithm will be performed. Implementation will be done using the JSP (Java Scripting Language) tool and SQL server 2008. |
| Solution will be performed in following way: |
| 1. Using RSA Algorithm: |
| User’s private data security and providing recommendations to user will be done by using RSA algorithm’s encryption and decryption process. |
| 2. Using ElGamal Algorithm: |
| Comparing similar users, similarity values with a threshold, according to that finding loyal/not loyal user and with these calculations providing recommendations to users will be done by ElGamal algorithm. |
| Therefore the survey says that Elgamal system is more suitable and advantageous than the Paillier system. Above stated problems like less security, complexity and inefficiency will be solved with the help of this Elgamal system. Compared to Paillier system, the Elgamal system i.e. Elgamal algorithm is much simpler and easy with independent partial private key is a factorization secret in Paillier encryption which makes it inefficient. |
| ElGamal Algorithm: |
| 1. Data from user |
| 2. Encrypt the data using ElGamal algorithm |
| a. Choose a large prime p with 150 digits |
| b. choose two random integers 1 ≤ q, x < p |
| c. Calculate y=qxmodp |
| d. Public key: p, q, y; private key: x |
| e. Encryption of a data R: choose a |
| Random t and compute c2=qtmod p and c1=ytRmod p |
| f. Cipher Text c= (c1, c2) |
| 3. Send cipher text to service provider |
| 4. Calculate Similarities between particular users with all other user |
| 5. Send similarities to privacy service provider |
| 6. Decrypt similarities |
| R=c1/c2x mod p+c2c1 |
| 7. Compute recommendation |
| a. Finding similar users |
| b. Computing the number L and sum of ratings of most similar users |
| c. Computing Recommendation |
| 8. Send recommendation to user. [15] |
| Example of Elgamal algorithm: |
| Alice wants to send message M=100 to Bob |
| 1. Choose a large Prime p=139 and q=3 |
| 2. Calculate Public key: |
| 44 = 312mod 139 |
| 3. Public key=44 and private key=12 |
| Choose random t =52 |
| Calculate t= 4452d 139 =112 |
| C1= 352 mod 139=38 |
| C2= 100 * 112 mod139= 80 |
| 4. C= (C1, C2) = (38, 80) |
| 5 Calculate t= 3812mod 139=112 |
| t-1 = 112-1 mod 139= 36 |
| 6. Recovers message |
| M=t-1C2 mod p= 36*80 mod 139=100 [16] |
CONCLUSION
|
| This paper includes a survey of the various techniques that have been applied previously for the security of user’s personal data. As Overall survey shows that the system used before uses Multiparty Computation technique that gives some problems or disadvantages. Therefore to avoid these problems we can use two algorithms that help us to benefit for the individual and business and compared to existing private recommendations system, this system is more secure, efficient and inexpensive. |
| |
Figures at a glance
|
 |
 |
| Figure 1a |
Figure 1b |
|
| |
References
|
- List of Social Networking Websites 2009 [Online]. Available: http://en.wikipedia.org/wiki/List_of_social_networking_websites
- Z. Erkin, M. Beye, T. Veugen, and R. L. Lagendijk, “ Generating Private Recommendations Efficiently Using Homomorphic Encryption and Data Packing", IEEE Transaction on Information Forensics and Security", Vol.7, No. 3, JUNE 2012.
- G. Adomavicius and A. Tuzhilin, “Toward the next generation of recommender systems: A survey of the state-of-the-art and possible extensions,” IEEE Trans. Knowl. Data Eng., vol. 17, no. 6, pp. 734–749, Jun. 2005.
- N. Ramakrishnan, B. J. Keller, B. J. Mirza, A. Y. Grama, and G. Karypis, “Privacy risks in recommender systems,” IEEE Internet Comput., vol. 5, no. 6, pp. 54–63, Nov./Dec. 2001.
- N. Kroes, “Digital agenda”, Brussels, May 19, 2011.
- S. Zhang, J. Ford, and F. Makedon,” Deriving private information from randomly perturbed ratings”. In Proceedings of the Sixth SIAM International Conference on Data Mining, pages 59–69, 2006.
- J. F. Canny. “Collaborative filtering with privacy via factor analysis”, In SIGIR, pages 238–245, New York, NY, USA, 2002, ACM Press.
- J. F. Canny. “Collaborative filtering with privacy”, In IEEE Symposium on Security and Privacy, pages 45–57, 2002.
- H. Polat and W. Du,“Privacy-preserving collaborative filtering using randomized perturbation techniques. In ICDM, pages 625–628, 2003.
- H. Polat and W. Du.,“SVD-based collaborative filtering with privacy”. In SAC ’05: Proceedings of the 2005 ACM symposium on applied computing, pages 791–795, New York, NY, USA, 2005, ACM Press.
- M.Atallah, M. Bykova, J. Li, K. Frikken, and M. Topkara, “Private collaborative forecasting and benchmarking,” in Proc. 2004 ACM Workshop on Privacy in the Electronic Society (WPES’04), New York, NY, 2004, pp. 103–114, ACM.
- Z. Erkin, M. Beye, T. Veugen, andR. L. Lagendijk, “Privacy enhanced recommender system,” in Proc. Thirty-First Symp. Information Theory in the Benelux, Rotterdam, 2010, pp. 35–42.
- Z. Erkin, M. Beye, T. Veugen, and R. L. Lagendijk, “Efficiently computing private recommendations,” in Proc. Int. Conf. Acoustic, Speech and Signal Processing (ICASSP), Prague, Czech Republic, May 2011, , pp. 5864–5867, 2011.
- P. Paillier, “Public-key cryptosystems based on composite degree residuosity classes,” in Proc. Advances in Cryptology (EUROCRYPT’ 99), ser. LNCS, J. Stern, Ed., May 2–6, 1999, vol. 1592, pp. 223–238, Springer.
- Online Available: http://en.wikipedia.org/wiki/ElGamal_encryption
- Online available: http://ta.ramk.fi/~jouko.teeriaho/cryptodict/Elgamal.pdf
|