ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
Somashekhar Swamy1, P.K.Kulkarni2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
Computed tomography (CT) is the technique that uses X-ray equipment to produce detailed images of section inside the animal or human body. CT scanning is very beneficial for detecting the diseases like cancers, tumors in human body. But noise and Blur are the major factors that degrade the quality of CT images and makes difficult to diagnose. Reconstructing the CT images is the way to overcome these problems. This paper presents the study of various techniques that are suitable to reconstruct the CT images, along with the performance evaluation of various techniques. This survey mainly focuses on most prominent techniques like filtering technique (discrete wavelets, complex wavelets, and median filter), artificial neural network approach for image reconstruction and Median filtering technique, also discussed other denoising and deblurring techniques. The aim of this survey is to provide useful information on various deblurring and denoising techniques and to motivate research to implement the effective algorithm.
KEYWORDS |
| Computed Tomography, De-noising, De-blurring |
I. INTRODUCTION |
| Computed tomography, more commonly known as a CT or CAT scan, is similar to X-rays for the diagnosing medical test, CT produces series of images or pictures of the body. CT scan has got significant role in medical field for detecting and analyzing diseases. CT scan is used to examine the chest, injuries, kidney, etc. CT images provide detailed, cross-sectional views of all types of tissue in our body, this makes easier to diagnose. But many of CT images suffer from deterioration in the quality of the image because of noise, blur deficiency. These degradations makes hard to analyze. Analysis of CT image is very essential to take decision. Bad analysis results in wrong decision, which results failure in detection. Removing noise and blur is very crucial. Researchers have been working for decades on reconstruction of CT images. |
| Image noise is random pixels scattered all over the regions of image. Source of noise generally comes from cameras and poor illumination. Noisy images provide less information. Blurs occur because of poor illumination, camera movement when capturing or object movement when capturing. Removing noise and blur is big challenge in image reconstruction. Most of the algorithms have disadvantage of information loss like, edge information, small spatial structures, etc. Preserving edges and small spatial structures in CT reconstruction is challenging task for researchers. Identifying tumors, cancer cells or small injuries is the main objective of analyst. But finding tumors or cancer cells in early stage is difficult, because in early stage spatial structure of tumor is very tiny in size [2, 14, 17]. |
| Various types of filtering technique used as a denoising tool such as wavelet based filtering [5, 7, 16, 19, 22], Median filtering [18], etc. Filtering is process of removing noisy components from the transformed image. For deblurring process sharpening the image to get clear structure of the object is included. All the researchers’ goal is to achieve high efficiency and accuracy in the performance of algorithm. But most of their respective algorithms have their own pros and cons also. Some reconstruction techniques are also briefly explained in this paper. |
II. WAVELET BASED FILTERING |
| Filtering is the traditional way of image denoising. It is a process of removing some of the coefficients of transformed image, those coefficients treated as noise. In proportion to actual image characteristic, noise statistical property and frequency spectrum distribution rule, people have developed many algorithms of diminishing noises, which are approximately divided into space and transformation fields. A data operation carried on the original image called space field and it processes the image gray value. Transformation field is responsible for image transformation, after the transformation coefficients are obtained and these coefficients are processed. Finally the output image is obtained by using inverse transformation as shown in Figure 1. Successful usage of wavelet transform might lessen the effect of noise or even overcome it completely. Wavelet transform is classified into two types, continuous wavelet transform and discrete wavelet transform. |
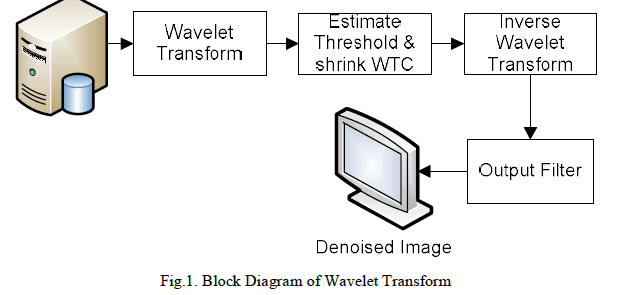 |
A. Discrete Wavelet Transform (DWT) |
| Marcin KocioÃâ¦Ãâek et.al, [24] proposed an image denoising technique based on DWT. It is a wavelet based denoising technique and used widely in the field of image construction. DWT is linear in nature that operates on a data vector and its length is an integer power of two, transforming it into a numerically different vector of the same length. DWT is a tool that separates data into different variations of frequency components and then finds every component with resolution matched to its scale. DWT is computed with a sequence of filtering followed by a factor 2 sub sampling as shown in Figure 2. |
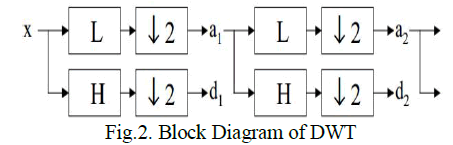 |
| H denotes the high pass filters and L denotes the low-pass filters, ↓ 2 represent sub sampling. Outputs of these filters are given by equations (1) and (2). |
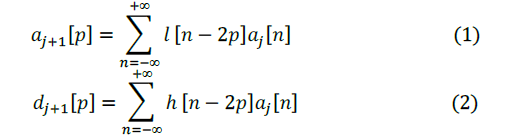 |
| Elements of aj are used for next level of transform and dj denotes coefficients, that determines the transformation result. Here l[n] denotes coefficients of low pass filters and h[n] denotes coefficients of high-pass filters. One assumption is to be taken, i.e. on scale j + 1 there is only half from number of a and d elements on scalej. So that, Transformation should be done until only two aïÿýïÿý elements remain in the signal. Finally coefficients of scaling function obtained. DWT mechanism is similar for all two-dimensional images. DWT is applied for rows and then applied for columns. Working of DWT is shown in Figure 3. DWT provides better spatial and spectral localization of image formation. |
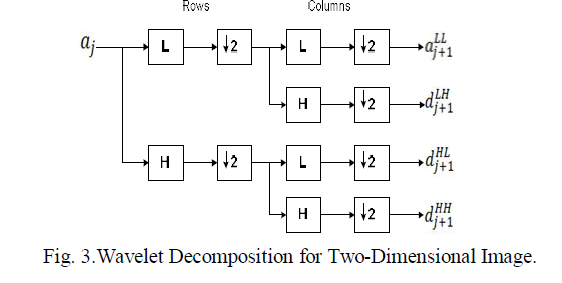 |
| DWT still it suffers from two serious disadvantages of shift invariant and no phase information. For reducing these disadvantages several solutions have been proposed, but the most agreeable solution is using Complex Wavelet Transform [7]. |
B. Dual-Tree Complex Wavelet Transform (DTCWT): |
| Ashish Khare et.al, [7] proposed a Dual-tree complex wavelet transform for denoising and deblurring. Denoising and deblurring using complex wavelet transform which includes 2 steps, first denoising the image using wavelet transformation and next apply deblurring algorithm to get the resultant de-noised image. The working of DT CWT is shown in Figure 4. |
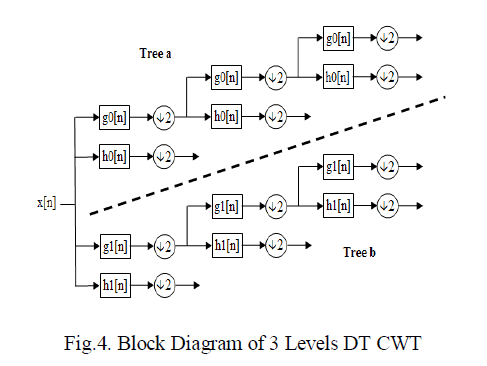 |
| For denoising of image, threshold based denoising scheme is used. Used threshold is complex in nature and also adaptive. It can be computed by estimating noise variation from the image. Threshold value is computed to both real and imaginary domain. Here soft-thresholding scheme is used for modification of wavelet coefficients. Inverse wavelet transform gives the output (de-noised) image. The denoising process of this stage introduces a small amount of blur in the image and it does not remove the original blur. Forward algorithm is used to remove noise from the image, but it gives inaccurate results when non-Gaussian noise exists. To overcome this problem author modified the algorithm is as follows: |
| ïÃÆÃË Applying regularized inverse filter to the original image. |
| ïÃÆÃË Estimate the noise variance |
| ïÃÆÃË Compute Daubechies Complex Wavelet transform of regularized inverse filtered image. |
| ïÃÆÃË Shrink the computed wavelet coefficients by adaptive complex threshold, by soft Thresholding. |
| ïÃÆÃË Perform wavelet domain filtering, which gives real and imaginary part of wavelet coefficients for deblurred image |
| ïÃÆÃË Apply Inverse wavelet transform that gives resultant deblurred image. |
C. Complex wavelets combined with Filtered Back-Projection (FBP): |
| V Thavavel et.al, [16] proposed a regularized reconstruction method which combines features from the Filtered Back- Projection (FBP) algorithm and regularization theory in CWT, filters have both complex and real coefficients Still, a further problem arises in attaining perfect reconstruction for complex wavelet decomposition above level 1. By using Dual-tree Complex wavelet transform (DT CWT) we can calculate the complex transform of a signal using two separate DWT decompositions. By obtaining both real as well as imaginary coefficients we can get more information. The filtering part of FBP performs Fourier-domain inversion followed by noise elimination in complex wavelet domain, to cater efficient estimate of the original image even with ill-conditioned systems. |
D. Haar wavelet and Daubechies wavelet: |
| Kanwaljot Singh Sidhu et.al, [23] proposed method involves Haar wavelet and Daubechies Transform for medical image denoising. The work comprise 5 sections namely, wavelet selection, threshold selection, decomposition of input image, reconstruction of image and comparison of PSNR. In wavelet selection Haar wavelets and Daubechies transform are selected for decomposition of signal. In threshold selection tested both hard and soft Thresholding. Haar wavelet is simple and old method used for signal transformation. Haar transformation decomposes non-continuous signal into two separate sub-signals. One sub-signal is a running average and other is a running difference. Haar wavelet is simple, fast and consumes less memory. |
| Set of scaling function in Daubechies wavelet is orthogonal in nature. Frequency responses are balanced in Daubechies wavelet and phase responses are non-linear. It has a property of overlapping windows and coefficients spectrum reflects at the high frequency changes. It is more efficient in removing noise and compressing audio signal. In the next step thresholding operation is used. Using thresholding a binary image can be created from gray values of gray image. Another use of thresholding is used to segment an image by setting all pixels whose intensity values are above a threshold to a foreground value and all the remaining pixels to a background value. Thresholding is classified into two categories: |
| 1. Hard Thresholding |
| Procedure of hard threshold is "keep or kill" and is appealing more possibly. Sometimes pure noise coefficients may come across the hard threshold. Hard Thresholding is used widely in medical image processing. |
| 2. Soft Thresholding |
| Soft threshold compresses the coefficients above the threshold in absolute value. The false structures in hard thresholding can be overcome by soft thresholding. |
| PSNR (Peak Signal to Noise Ratio) is calculated by comparing both degraded input image and restored image. For PSNR calculation following equation is used. |
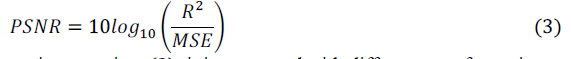 |
| After getting PSNR values using equation (3), it is compared with different transformation techniques. |
E. Average Filter Or Mean Filter |
| Important features are characterized by large wavelet coefficient across scales in most of the timer scales. Ghosh et.al, [5] proposed an image-to-image transformation designed to smoothen or flatten an image by reducing the rapid pixelto- pixel variation in grey-levels. Smoothing may be accomplished by applying an averaging or mean mask that computes a weighted sum of the pixel grey-levels in a neighborhood and replaces the centre pixel with that grey-level. The image is blurred and its brightness retained as the mask coefficients are all-positive and sum to one. The mean filter is one of the most basic smoothing filters. Like other convolutions it is based around a kernel, which represents the shape and size of the neighborhood to be sampled. When calculating the mean smoothing is applied subject to the condition that the centre pixel grey-level is changed only if the difference between its original value and the average value is greater than a preset threshold. This causes the noise to be smoothed with a less blurring in image detail. Mean filters thus find extensive use in blurring and noise removal. Blurring is usually a preprocessing step bridging gaps in lines or curves, helping remove small unwanted detail before the extraction of relevant larger objects. |
| In order to succeed over the bad influence of noise and shading, there is a need to choose right algorithm being employed. Most of algorithm’s limitation is that they show efficient results on only certain datasets. By considering the above problem, Shruti bhargava et.al, [19] proposed a hybrid filter, by combining the set of filters such as median filter, average filter and diffusion filter on adaptive wavelet thresholding based de-noised medical data in order to enhance results. This algorithm is tested on different types of medical datasets like Ultrasound, SPECT, MRI, CT and PET. |
III. MEDIAN FILTER |
| Median filtering is a nonlinear method useful in lessening impulsive or salt-and-pepper noise. Additionally, it is easy for edge preserving in a picture whereas reducing random noise. Impulsive or salt-and pepper noise will occur because of random bit error in an exceedingly channel. In an exceedingly median filter, a window slides on the image and also the median intensity value of the pixels among the window becomes the output intensity of the pixel being processed. Median filtering is not appropriate for encountering high impulsive noise. Suman Shrestha et.al, [18] proposed a technique called decision based Median filter, which is more effective in removing impulsive noise. The decision based median filtering method processes the corrupted image pixels by detecting whether the pixel value is a corrupted one. This decision is made similar to the one made for adaptive median filtering technique, i.e. based on whether the pixel value to be processed lies between the minimum and the maximum value inside the window to be processed. If the pixel value lies between the minimum and the maximum value in the window, the pixel remains as it is (i.e. the pixel is noise free), otherwise the pixel is replaced with the median value of the window or its neighborhood pixel value. The decision based filtering algorithm is as stated below: |
 |
IV. NEURAL NETWORKS APPROACH |
| ANN is a mathematical or computational model that attempts to model the functional features of biological neural networks. These networks consist of an interconnected group of artificial neurons to process input information. ANN can be an adaptive system that changes its construction based on external or internal information that flows through the network during the learning phase. ANNs are usually used to model complex relationships between inputs and outputs which can be identified mathematically. ANN has good learning ability. Learning algorithms seek through the solution space in order to find a cost function that has the smallest possible measure of how far away from an optimal solution to the problem that we want to solve. Figure 5 represents the structure of ANN. Each circles treated as nodes i.e. artificial neurons and arrow is the connection mapping to each input and output nodes. |
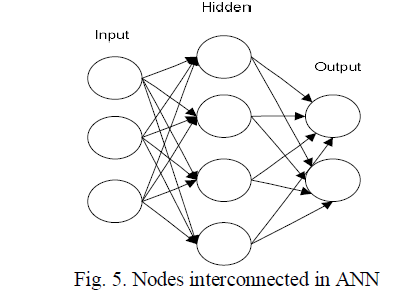 |
A. Neural Network In Image Reconstruction: |
| Artificial neural network is a machine learning approach used for pattern recognition. ANN is used for deblurring the images [4, 8, and 10]. Yazeed A et.al, [8] proposed a Artificial neural network as a denoising tool. The technique includes using both mean and median statistical functions for calculating the output pixels of the training pattern of the neural network. The system was trained with different types of degraded images and test images with different noise levels were used. |
| Neeraj Kumar et.al, [4] proposed an algorithm with three layer neural networks with back propagation. To reconstruct the enhanced image using neural network, we need to have a blurred image and correlated original image. They considered original image as Markov Random field (MRF) and blurred image as degraded version of MRF. The complicate is in establishing the functional mapping between original image and noisy blurry image, which is usually non-linear in nature. To do that, method needs to pick a 3×3 patch form blurred image and the center pixel of the corresponding patch form the original image. The desired mapping is learnt by giving blurred patch as input to the neural network and the center pixel of the original patch as the output. Training samples is generated by shifting the center pixel of 3×3 patch by one pixel in either direction for both the blurred patch (training input) and the original patch (target output). The system achieves desired mapping by using a small number of sigmoid basis functions. The system checks that learnt mapping captures the orientation and distance from the center of an edge passing through the original patch. This is showed in Figure 6. Like this, the function can efficiently reconstruct the edge in the deblurred patch. |
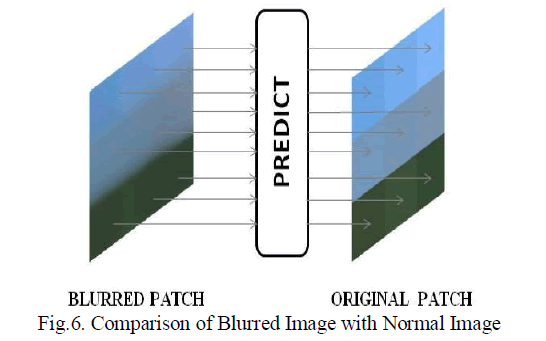 |
| P.Subashini et.al, [10] proposed a back propagation neural network for deblurring images. Along this gradient decent rule is used which consists of three layers. This procedure uses highly nonlinear back propagation neuron for image restoration to get a high quality restored image and attains fast neural computation, less computational complexity due to the less number of neurons used and quick convergence without long training algorithm. The algorithm achieved better result when comparing traditional image reconstruction approach. |
V. OTHER RECONSTRUCTION APPROACHES |
A. Multi-resolution Based Method: |
| Gerald zauner et.al, [1] proposed an image denoising technique based on Multi-resolution, that uses wavelet filters and platelets. It focuses on the tiny objects in the CT images. Because of noise small objects like holes, marks become hidden and invisible to the human eye. To overcome this problem, platelet filtering is used. Even though wavelet provides efficient result in various applications, it still suffers from less edge information. Also, most of the waveletbased approaches are based on Gaussian approximations and which gives bad result when low count levels are encountered. By observing this condition new multiscale image representation based on platelets are presented. The platelet is based on the wedge-let-approach. Each wedge-let is defined on a dynamic square with certain edge-points. Instead of constant partitions of approximations, planar surfaces are introduced by platelets and in this way additionally gradients. This representation is coded in tree structure and its adaptive ‘pruning’ process removes portion of noisy signals. Compared to Linear filter method, the platelet filter has got better result. After the linear filtering, small spatial structures have been almost removed. Platelet filter still holds the information of small spatial structures. |
B. Edge Preserving Reconstruction techniques: |
| Most of the image reconstruction algorithms have the problem of information loss. After the reconstruction process, the noise will be removed, but some significant information like edges, tiny spatial structures will also be removed. Preserving the edges is one of the challenges in image reconstruction. Using nonlocal regularization [2, 14] we can preserve edges in the images. Daniel Yu et.al, [2] proposed an edge-preserving tomography reconstruction algorithm with nonlocal Regularization. Reconstruction process includes smoothing, that sometimes reduce the edge information. Commonly small differences between neighboring pixels are often due to noise and large differences are because of edges. This observation is a basis for many edge preserving algorithms. Most edge preserving algorithms consists of large line-site model. In each pixel local neighborhood information is passed for estimation of edge, i.e., a penalty is assigned to each pixel of group. |
| Ming Jiang et.al, [14] presented a new method called blind deblurring algorithm based on the edge-to-noise ratio, which has been applied to improve the quality of spiral CT images. Since the discrepancy measure used to quantify the edge and noise effects is not symmetric, there are several ways to formulate the edge-to-noise ratio. Daniel Yu et.al, made a comparative study on different edge-to-noise ratio for proposed de-blurring algorithm. |
C. Laplacian sharpening filter and iterative Richardson-Lucy Algorithms: |
| Zohair Al-Ameen et.al, [3] proposed an algorithm for reducing Gaussian blur from the CT images by combining Laplacian sharpening filter and iterative Richardson Lucy Algorithm. Gaussian blur is added to degrade the CT image which is applied after deblurring algorithm. Deblurring procedure includes diminution of blur and transform image to sharpened form. By integrating Laplacian sharpening filter and iterative Richardson Lucy algorithm CT image is processed. The algorithms tested with several medical CT images that are degraded by artificial (Gaussian blur) and natural blurs. |
| 1. Laplacian Sharpening Filter: |
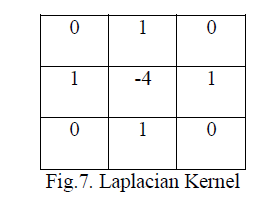
| Laplacian filter is normally used to sharpen the image by highlighting edge information of the images. Here 3x3 matrixes is the Laplacian kernel which is convolved to the image. The result of this convolution is treated as mask that will be the difference of degraded image and the original image. There are various Laplacian kernels sorts. New sort of kernel is shown in Figure 7. |
 |
 |
| optimization and adaptive techniques, which makes it very attractive in control problems, particularly for dynamic nonlinear systems. Sugeno-type fuzzy systems are popular general nonlinear modeling tools because they are very suitable for tuning by optimization and they employ polynomial type output membership functions, which greatly simplifies de-fuzzification process. The fuzzy inference is performed on the impulsive noisy input image pixel by pixel. Each non-linear noisy pixel is independently processed by the Decision Based Switching Median Filter (DBSMF) and the canny edge detector before being applied to the fuzzy network. Hence, in the structure of the proposed operator, we can give in the input in three phases one is much noise, second would be the blur, and third would be the combination of both. We can represent these by any of the convenient notations. Each possible combination of inputs and their associated membership functions is represented by a rule in the rule base of fuzzy network. |
VI. CONCLUSIONS |
| For accurate information, de-noising and de-blurring is very much essential. The survey in this paper discusses about the major approaches for image reconstruction, particularly in the field of medical image processing. All the algorithms are efficient to improve the quality of degraded image. Algorithm has to be still more effective to obtain more accurate diagnostic information. Also there is a need to improve algorithms to make system robust. In view of this sufficient information about various methodologies in denoising and deblurring of different types of medical images are presented in this paper. |
References |
|