Keywords
|
| Mobile ad hoc networks, intrusion response, risk aware, dempster-shafer theory. |
INTRODUCTION
|
| Mobile Ad hoc Networks (MANET) are to set up wireless communication in environments without a predefined infrastructure or centralized administration. MANET has been normally deployed in adverse and hostile environments where central authority point is not necessary. Another unique characteristic of MANET is the dynamic nature of its network topology which would be frequently changed due to the unpredictable mobility of nodes. Furthermore, each mobile node in MANET plays a router role while transmitting data over the network. Hence, any compromised nodes under an adversary’s control could cause significant damage to the functionality and security of its network since the impact reduce the performing of the routing tasks. |
| Several work [1], [2] addressed the intrusion response actions in MANET by isolating uncooperative nodes based on the node reputation derived from their behaviours. In MANET scenario, improper countermeasures may cause the unexpected network partition, bringing additional damages to the network infrastructure. The notion of risk can be adopted to support more adaptive responses to routing attacks in MANET [3]. Wang et al. [4] proposed a naive fuzzy cost-sensitive intrusion response solution for MANET. In this paper, we seek a way to bridge this gap by using Dempster-Shafer mathematical theory of evidence (D-S theory), which offers an alternative to traditional probability theory for representing uncertainty [5]. D-S theory has been adopted as a valuable tool for evaluating reliability and security in information systems and by other engineering fields [6], [7], where precise measurement is impossible to obtain or expert elicitation is required. As in [8], [9], [10], [11], Dempster’s rule of combination has several limitations, such as treating evidences equally without differentiating each evidence and considering priorities among them. To deal with these limitations in MANET intrusion response scenario, a new Dempster’s rule of combination with a notion of importance factors (IF) in D-S evidence mode is introduced. |
BACKGROUND
|
OLSR Protocol
|
| Protocols generally fall into two major categories: |
| 1 .Reactive routing protocol, |
| 2. Proactive routing protocol |
| In reactive routing protocols, such as Ad hoc On Demand Distance Vector (AODV) protocol nodes find routes only when they have to send data to the destination node whose route is unknown. In proactive routing protocols, such as OLSR, nodes obtain routes by periodic exchange of topology information with other nodes and maintain route information all the time. |
| OLSR protocol is a variation of the pure Link-state Routing (LSR) protocol and it is designed specifically for MANET. OLSR protocol achieves optimization over LSR by the using of multipoint relay (MPR) to provide an efficient flooding mechanism by reducing the number of transmissions required. Unlike LSR, where every node declares its links and forward messages for their neighbors, only nodes selected as MPR nodes are responsible for advertising, as well as forwarding an MPR selector list advertised by other MPRs. |
Routing Attack on OLSR
|
| Attacks against MANET can be classified into passive or active attacks, based on their behavior. Attacks can be further categorized as outsider or insider attacks. With respect to the target, attacks could be also divided into data packet or routing packet attacks. In routing packet attacks, attackers could not only prevent existing paths from being used, but also spoof non-existing paths to lure data packets to them. |
EXTENDED DEMPSTER-SHAFER THEORY OF EVIDENCE
|
| The D-S mathematical theory of evidence is both a theory of evidence and a theory of probable reasoning. The limitations of the Dempster’s rule of combination, |
| 1 .Associative |
| 2. Nonweighted. |
| D-S theory will overcome both the limitations of Dempster’s rule. |
Importance Factors and Belief Function
|
| Suppose Θ is a finite set of states, and let 2Θ denote the set of all subsets of Θ. D-S theory calls Θ, a frame of discernment. When a proposition corresponds to a subset of a frame of discernment, it implies that a particular frame discerns the proposition. First, we introduce a notion of importance factors. |
| Definition 1: Importance factor (IF) is a positive real number associated with the importance of evidence. IFs are derived from historical observations or expert experiences. |
| Definition 2: An evidence E is a 2-tuple <m; IF> where m describes the basic probability assignment [5]. Basic probability assignment function m is defined as follows: |
| M(?)=0 |
| And |
| Definition 3: Extended D-S evidence model with importance factors: Suppose E1 <m1, IF1> and E2 <m2, IF2> are two independent evidences. Then, the combination of E1 and E2 is Dempster’s rule of combination with importance factors. |
 |
RISK-AWARE RESPONSE MECHANISM
|
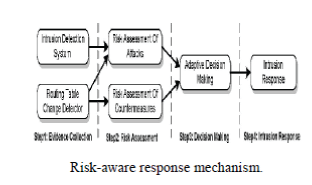
| In this section, we perform an adaptive risk-aware response mechanism based on quantitative risk estimation and risk tolerance. Instead of applying simple binary isolation of malicious nodes, this approach adopts an isolation mechanism in a temporal manner based on the risk value. Risk assessment is performed with the extended D-S evidence theory. |
Overview
|
| Because of the infrastructure-less architecture of MANET, our risk-aware response system is distributed, which means each node in the system makes its own response decisions based on the evidences and its own individual benefits. Therefore, some nodes in MANET may isolate the malicious node, but others may still keep in cooperation with due to high dependency relationships. Risk aware response mechanism is divided into the following steps. |
| 1. Evidence collection. |
| 2. Risk assessment. |
| 3. Decision making. |
| 4. Intrusion response. |
 |
Response to Routing Attacks
|
| We use two different responses to deal with different attack methods: routing table recovery and node isolation. Routing table recovery includes local routing table recovery and global routing recovery. Local routing recovery is performed by victim nodes that detect the attack and automatically recover its own routing table. Global routing recovery involves with sending recovered routing messages by victim nodes and updating their routing table based on corrected routing information in real time by other nodes in MANET. |
Adaptive Decision Making
|
| This module is based on quantitative risk estimation and risk tolerance. The response level is additionally divided into multiple bands. Each band is associated with an isolation degree, which presents a different time period of the isolation action. The response action and band boundaries are all determined in accordance with risk tolerance and can be changed when risk tolerance threshold changes. The upper risk tolerance threshold (UT) would be associated with permanent isolation response. The lower risk tolerance threshold (LT) would remain each node intact. The band between the upper tolerance threshold and lower tolerance threshold is associated with the temporary isolation response, in which the isolation time (T) changes dynamically based on the different response level given by (18) and (19).where n is the number of bands and i is the corresponding isolation band. |
Methodology and Metrics
|
| In order to evaluate the effectiveness of our adaptive risk-aware response solution, we divided the simulation process into three stages and compared the network performance in terms of six metrics. The following describes the activities associated with each stage: |
| Stage 1- Before attack. Random packets were generated and transmitted among nodes without activating any of them as attackers. This simulation can present the traffic Patterns under the normal circumstance. |
| Stage 2- After attack. Specific nodes were set as attackers which conducted malicious activities for their own profits. However, any detection or response is not available in this stage. This simulation process can present the traffic patterns under the circumstance with malicious activities. |
| Stage 3- After response. Response decisions for each node were made and carried out based on three different mechanisms. |
| Six metrics are computed [21] for each simulation run: |
| Packet delivery radio: The ratio between the number of packets originated by the application layer CBR sources and the number of packets received by the CBR sink at the final destination . |
| Routing cost: The ratio between the total bytes of routing packets transmitted during the simulation and the total bytes of packets received by the CBR sink at the final destination. |
| Packet overhead: The number of transmitted routing packets; for example, a HELLO or TC message sent over four hops would be counted as four packets in this metric. |
| Byte overhead: The number of transmitted bytes by routing packets, counting each hops similar to Packet Overhead. |
| Mean latency. The average time elapsed from “when a data packet is first sent” to “when it is first received at its destination.” |
| Average path length: This is the average length of the paths discovered by OLSR. It was calculated by averaging the number of hops taken by each data packet to reach the destination. |
RELATED WORK
|
| When Risk-aware approaches comes to make response decisions there always exists uncertainty which leads to unpredictable risk, especially in security and intelligence area. Risk-aware approaches are introduced to handle this problem by balancing action benefits and damage trade-offs in a quantified way. |
| Cheng et al. [3] presented a fuzzy logic control model for adaptive risk-based access control. Teo et al. Introduce Dynamic risk-aware mechanism to determine whether an access to the network should be denied or permitted. However, risk assessment is still a nontrivial challenging problem due to its subjective knowledge, objective evidence, and logical reasoning. Wang et al. [4] proposed a naive fuzzy cost-sensitive intrusion response solution for MANET. This cost model took subjective knowledge and objective evidence into account but omitted the combination of two properties with logical reasoning. Mu et al. [7] adopted Dempster-Shafer theory to measure the risk of attacks and responses. However, as identified in [8], their model with Dempster’s rule treats evidences equally without differentiating them from each other. To address this limitation, a new Dempster’s rule of combination with a notion of importance factors in D-S evidence model is introduced. |
| |
References
|
- Y. Sun, W. Yu, Z. Han, and K. Liu, “Information Theoretic Framework of Trust Modelling and Evaluation for Ad Hoc Networks,” IEEE J. Selected Areas in Comm., vol. 24, no. 2, pp. 305-317, Feb. 2006.
- M. Refaei, L. DaSilva, M. Eltoweissy, and T. Nadeem, “Adaptation of Reputation Management Systems to Dynamic Network Conditions in Ad Hoc Networks,” IEEE Trans. Computers, vol. 59, no. 5, pp. 707-719, May 2010.
- P. Cheng, P. Rohatgi, C. Keser, P. Karger, G. Wagner, and A. Reninger, “Fuzzy Multi-Level Security: An Experiment on Quantified Risk- Adaptive Access Control,” Proc. 28th IEEE Symp. Security and Privacy, 2007.
- S. Wang, C. Tseng, K. Levitt, and M. Bishop, “Cost-Sensitive Intrusion Responses for Mobile Ad Hoc Networks,” Proc. 10th Int’l Symp. Recent Advances in Intrusion Detection (RAID ’07), pp. 127- 145, 2007.
- G. Shafer, A Mathematical Theory of Evidence. Princeton Univ., 1976.
- L. Sun, R. Srivastava, and T. Mock, “An Information Systems Security Risk Assessment Model under the Dempster-Shafer Theory of Belief Functions,” J. Management Information Systems, vol. 22, no. 4, pp. 109-142, 2006.
- C. Mu, X. Li, H. Huang, and S. Tian, “Online Risk Assessment of Intrusion Scenarios Using D-S Evidence Theory,” Proc. 13th European Symp. Research in Computer Security (ESORICS ’08), pp. 35-48, 2008.
- K. Sentz and S. Ferson, “Combination of Evidence in Dempster- Shafer Theory,” technical report, Sandia Nat’l Laboratories, 2002.
- L. Zadeh, “Review of a Mathematical Theory of Evidence,” AI Magazine, vol. 5, no. 3, p. 81, 1984.
- R. Yager, “On the Dempster-Shafer Framework and New Combination Rules_1,” Information Sciences, vol. 41, no. 2, pp. 93- 137, 1987.
- H. Wu, M. Siegel, R. Stiefelhagen, and J. Yang, “Sensor Fusion Using Dempster-Shafer Theory,” Proc. IEEE Instrumentation and Measurement Technology Conf., vol. 1, pp. 7-12, 2002.
- T. Clausen and P. Jacquet, “Optimized Link State Routing Protocol,” Network Working Group, 2003.
- C. Perkins, E. Belding-Royer, and S. Das, “Ad Hoc On-Demand Distance Vector Routing,” Mobile Ad-Hoc Network Working Group, vol. 3561, 2003.
- H. Deng, W. Li, and D. Agrawal, “Routing Security in Wireless Ad Hoc Networks,” IEEE Comm. Magazine, vol. 40, no. 10, pp. 70- 75, Oct. 2002.
- Y. Hu and A. Perrig, “A Survey of Secure Wireless Ad Hoc Routing,” IEEE Security and Privacy Magazine, vol. 2, no. 3, pp. 28- 39, May/June 2004.
|