Apriori algorithm is a classical algorithm of association rule mining and widely used for mining association rule which uses frequent item. Based on the Apriori algorithm analysis and research, this paper points out the main problems on the application, and puts forward the improved This paper presents an improved Apriori algorithm to increase the efficiency of generating association rules.
Keywords |
| association rules,Apriori algorithm, frequent items |
INTRODUCTION |
| Data mining is a kind of process of decision support. Itgets the potential and useful information and acknowledges from
practical application data which is large, incomplete, noisy, ambiguous and random. Data mining relates to extracting a
large of data from database, transforming, analyzing and modeling handling these data, and withdrawing the critical
data to aid decision making. Mining association rules is an important issue in data mining [1]. |
| R. Agrawal et al in 1993 proposed the famous the Apriori algorithm based on frequent item set [2,3], then the most
algorithms are all based on the basic algorithm for improvements or derivative variant of the algorithm [4,5]. An
improved association rule is proposed in this paper, which uses the intersection operation to generate frequent item sets,
which lays the basis of enhancing the performance of mining algorithm based on association rules. This algorithm only
needs to scan the database one time and also greatly reduce the number of candidates of frequent itemsets. |
ASSOCIATION RULE |
| Association rules can be de scripted formally as follows [6], |
| Assuming I=(i1, i2, …, im) is a collection of m different attributes, in the given database D, each record T is
acollection of a set of attributes of 1. That is T ⊆; I, T has aunique identifier TID. If X ⊆ I and X ⊆ T, T includes
X. Anassociation rule is the formula as X ⊆ Y, X ⊆ I, Y ⊆ I and Xn Y = <D . It indicates that if X appears in a
transaction, Y willbe lead to appear in the same transaction inevitablely. X is called the precondition of the rules, and Y
the result of the rules. |
| Itemsets Support |
| Times when an itemset appears in the transaction datasets is called support number or support for the count. Support is
divided by the total number of transactions, which is called the support of Itemsets. It can be defined by symbols as
follows: |
| Support(X ⇒Y) = P(X U Y) |
| Support(X ⇒. Y) refers to the probability of X and Y which appear in the D at the same time.P(X) refers to the
probability of X which appears in the dataset D, the same as P(Y). |
| Frequent Itemsets |
| If support of a itemset is greater than or equal to pre – defined minimum support threshold, the set of these itemsets are
called frequent itemset[7]. |
| There are two important basic measures for association rules, support(s) and confidence(c). Since the database is large
and users concern about only those frequently purchased items, usually thresholds of support and confidence are
predefined by users to drop those rules that are not so interesting or useful. The two thresholds are called minimal
support and minimal confidence respectively. Support(s) of an association rule is defined as the percentage/fraction of
records that contain X ∪ Y to the total number of records in the database. Suppose the support of an item is 0.1%, it
means only 0.1 percent of the transaction contain purchasing of this item. Confidence of an association rule is defined
as the percentage/fraction of the number of transactions that contain X ∪ Y to the total number of records that contain
X.Confidence is a measure of strength of the association rules, suppose the confidence of the association rule X⇒Y is
80%, it means that 80% of the transactions that contain X also contain Y together. In general, a set of items (such as the antecedent or the consequent of a rule) is called an itemset. The number of items in an itemset is called the length of an
itemset. Itemsets of some length k are referred to as k-itemsets. |
| • The set of candidate k-itemsets is generated by 1-extensions of the large (k -1)- itemsets generated in the previous
iteration. |
| • Supports for the candidate k-itemsets are generated by a pass over the database. |
| • Itemsets that do not have the minimum support are discarded and the remaining itemsets are called large k-itemset |
APRIORY ALGORITHM |
| General Process |
| Association rule generation is usually split up into two separate steps: |
| 1. First, minimum support is applied to find all frequent itemsets in a database. |
| 2. Second, these frequent itemsets and the minimum confidence constraint are used to form rules. |
| While the second step is straight forward, the first step needs more attention. |
| Finding all frequent itemsets in a database is difficult since it involves searching all possible itemsets (item
combinations). The set of possible itemsets is the power set over I and has size 2n − 1 (excluding the empty set which is
not a valid itemset). Although the size of the powerset grows exponentially in the number of items n in I, efficient
search is possible using the downward-closure property of support (also called anti-monotonicity) which guarantees
that for a frequent itemset, all its subsets are also frequent and thus for an infrequent itemset, all its supersets must also
be infrequent. Exploiting this property, efficient algorithms (e.g., Apriori and Eclat) can find all frequent itemsets. |
| Apriori uses breadth-first search and a tree structure to count candidate item sets efficiently. It generates candidate item
sets of length k from item sets of length k − 1. Then it prunes the candidates which have an infrequent sub pattern.
According to the downward closure lemma, the candidate set contains all frequent k-length item sets. After that, it
scans the transaction database to determine frequent item sets among the candidates. |
| Apriori, while historically significant, suffers from a number of inefficiencies or trade-offs, which have spawned other
algorithms. Candidate generation generates large numbers of subsets (the algorithm attempts to load up the candidate
set with as many as possible before each scan). Bottom-up subset exploration (essentially a breadth-first traversal of the
subset lattice) finds any maximal subset S only after all 2 | S | − 1of its proper subsets. |
ANALYSIS OF PROBLEM |
| Finding out the strong associate rule base on the minsupport and minconfidence which were appoint by user, and it can
divide into two questions: |
| 1) Find out the frequent itemsets: Use the minsupport to find all the frequent itemsets which not less than the
minsupport. In fact, they will contain each other. |
| 2) Produce the association rules: Find out the association rules which confidence not less than the minconfidence is in
the largest frequent itemsets. So, how to find out the frequent itemsets as soon as quickly, is the focus of association
rule mining. |
| There are two important natures in the association rule mining [8][9]: |
| 1: If itemsets X is a frequent itemsets, then all of its not-empty subsets |
| 2: If itemsets X is not a frequent itemsets, then all of its supersets are not frequent itemsets. |
APRIORY BASED ON MATRIX |
| The algorithm based on the matrix use matrix to describe the each affair in the database, so we just deal with the matrix
to count the support of the candidates of frequent itemsets, and do not need to scan the database again. |
| Here count the support quickly using the “AND operation [10] |
| The “AND operation” is to AND the rows according to the items in the candidate of frequent itemsets in the matrix,
then add the result of the AND, and the result is the support. For example, we just AND the row “a” and row “c” in the
matrix when we want to count the support of itemset {a, c}, and add the result, so we can get the support of it. |
| Process description: |
| 1. Convert the affair database contained i items and t affairs to a matrix which has i+1 rows and i+1 1 columns, the fist
column notes items and the first row notes affairs. |
| Then according to the minsupport simplified the matrix. When the sum of an item less than the minsupport, the item
will not be in any frequent itemsets, delete the row contained the item, . The matrix through the step is marked as the
initial matrix |
| 2. The largest frequent itemsets is a frequent itemsets which contains the most items than others. According the nature
1, it will be easier to find the frequent itemsets contained fewer items if we know the largest frequent itemsets |
| 3.Finding out the affair in the matrix which has the most items and the number of items is marked as K. If the number
of affairs which the number of the items not less than the K less than the minsupport, which means the largest frequent
itemsets cannot contain K items, so we should consider the affair which has K-1 items and use the K to mark the K-1.
We use this method until we find out the K that the number of affairs is not less than the minsupport. |
| a)Use recursive algorithm to simplify the Matrix |
| Delete the column which the number of items less than the K. Delete the row which the number of affairs less than the
minsupport.If it have not changed the Matrix we should mark the Matrix as NewMattix and go to the step . If the
Matrix is empty, which means there aren’t K-frequent itemsets. |
| b)Select an affair “t” in the NewMatrix and select K items in the t to form an itemsets, then Using the AND operation
count the Support of the itemsets. If its support is not less than the minsupport, the itemsets is a K-frequent itemsets. Or
else it is not. Then we again select the K items in the t which is not the same as the former and judge the support. Use
this method until there is no the different K items in the t. Now, we can delete the column contained the t and simplify
the NewMatrix. Then, use the same way to deal with the other affairs in the NewMatrix and the itemsets which has
been counted should not be considered again. Use this way until the NewMatrix is empty. If there are not K-frequent
itemsets, we should go to the step a) and consider the affair which has K-1 items. |
| 3. Using the Matrix finds out all the other frequent itemsets from 2-frequent itemsets to K-1-frequent itemsets, and the
method is similar to the Apriori algorithm. But should simplify the Matrix which made counting the support easier. |
RESULT OF ANLYSIS |
| In our experiment we select the supermarket data to to study the object. The supermarket database 7 different items and
contain 4000 transaction. To find out the efficiency of new proposed algorithm first we use normal apriori algorithm,
then we use improved apriori algorithm. |
Algorithm Comparison: |
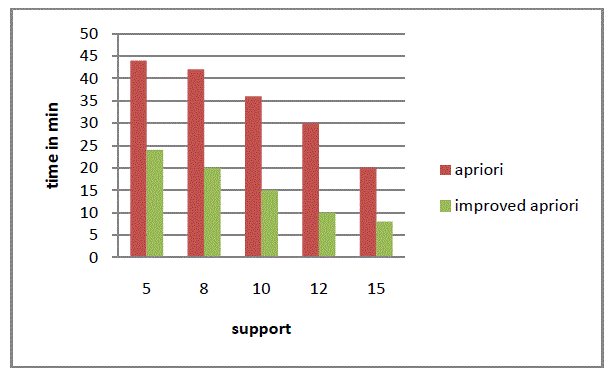
| Fig 1 shows the execution time of both apriori algorithm and improved apriori algorithm ,if we compared algorithm at
different support execution time required for normal apriori algorithm take more as compaired to improved algorithm
based on matrix. |
| The algorithm based on matrix don’t scan database frequently, which reduce the spending of I/O. So the new algorithm
is better than the Apriori in the time complexity. |
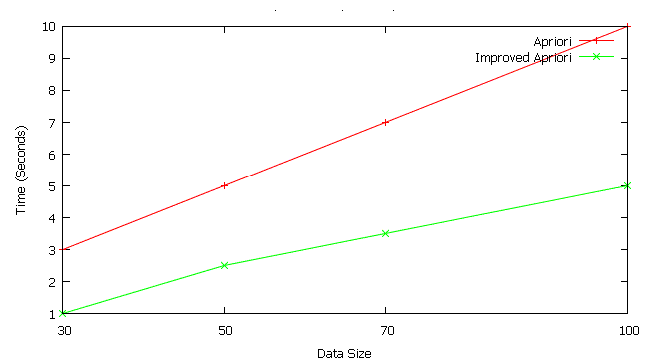
| As shown in the graph as we increase the size of the data base time to generate the rules in apriory algorithm take
more as compared to improved apriori method. |
CONCLUSION |
| The classical apriori algorithm suffers due to implementation complexity for JOIN & PRUNING. The algorithm based
on the matrix is better than the Apriori both in time and space. The matrix effectively indicate the affairs in the database
and uses the “AND operation” to deal with the matrix to produce the largest frequent itemsets and others. It needn’t
scan the database time and again to lookup the affairs, and also greatly reduce the number of candidates of frequent
itemsets. The new algorithm is better than the Apriori in the time complexity. Through this algorithm is good at finding
the frequent itemsets which support is small. The improved algorithm obtains the bonus time of calculating and
promotes the efficiency of computing. |
| |
Figures at a glance |
 |
 |
| Figure 1 |
Figure 2 |
|
| |
References |
- David Hand,Heikki Mannila,Padhraic Smyth. Principles of Data Mining[M]. translater Yinkun Zhang. Beijing: Mechanical Industry Press. 2003: 272-284.
- R Agrawal. Mining Association Rules Between Sets of Items inLarge Databases[C] .Washington: Proceedings of the ACMSIGMOD International Conference Management of Data, 1993 :207-216.
- Agrawal R, Srikant R. Fast algorithms for mining association rulesin large databases [A].Proc. of the 20th Int’l Conf on Very LargeData Bases.
[c]. Santiago: Morgan Kaufmann, 1994:478~499
- Z.Xu,S. Zhang. Mining Association Rules in an optimized Apriorialgorithm [J] Computer Engineering.2003, 29(19):83-85.
- G. Grahne, J.Zhu, Efficiently using prefix-trees in mining frequent itemsets. In Proc. ICDM’03 Int. Workshop on Frequent Itemsets Mining Implementations (FIMI’03), Melbourne, FL, Nov. 2003
- XIAO Bo, XU Qian-Fang, LIN Zhi-Qing, GUO Jun, LI Chun-Guang. Credible Association Rule and Its Mining Algorithm Based on Maximum Clique[J]. Journal of Software, 2008, 19(10): 2597-2610.
- XIA Ying, ZHANG Jun, WANG Guo-yin. Spatio-temporal Association Rule Mining Algorithm and its Application in Intelligent Transportation System[J]. Computer Science, 2011, 38(9): 173-176.
- Chen Wenwei. Data warehouse and data mining tutorial [M]. Beijing: Tsinghua University Press. 2006
- Zhu Yixia, Yao Liwen, Huang Shuiyuan, Huang Longjun. A association rules mining algorithm based on matrix and trees[J]. Computer science. 2006, 33(7):196-198
- Tong Qiang, Zhou Yuanchun, Wu Kaichao, Yan Baoping. Aquantitative association rules mining algorithm[J]. Computer engineering. 2007, 33(10):34-35
|