The wireless sensor node is a tiny device that is used to capture environment information. Sensor devices are used to capture temperature and pressure details from the environment. Sensors are used to cooperatively monitor physical or environmental conditions. Computing and tracking the spatial-average of the sensor measurements are estimated over a region of the WSN. Sensor faults and heterogeneous measurement noise factors affects the sensor data average process. Robust averaging fixed-point iteration algorithm is used to compute a weighted average of sensor measurements with noise and faults. Each sensor performs projections on its sensor measurements to produce a lower bandwidth compressed data stream. Data approximation process is used to assign relevant data values for missed or noisy data values. The sensors in the WSN use random projections to compress the data and send the compressed data to the data fusion centre. The data fusion centre only need to perform decompression once to compute the robust average to reducing the computational requirements. The compressive data collection scheme is enhanced with Bayesian approach to support projection count prediction. Sensing and transmission coverage factors are integrated in the data collection process. Data projection accuracy is improved with frequent pattern identification mechanism. The data collection scheme is tuned to support scheduling schemes to increase network lifetime.
INTRODUCTION |
| A wireless sensor network (WSN) is a wireless network consisting of spatially distributed autonomous devices
using sensors to cooperatively monitor physical or environmental conditions The development of wireless sensor networks
was originally motivated by military applications such as battlefield surveillance In addition to one or more sensors, each
node in a sensor network is typically equipped with a radio transceiver or other wireless communications device, a small
microcontroller, and an energy source, usually a battery. The envisaged size of a single sensor node can vary from shoeboxsized
nodes down to devices the size of grain of dust, although functioning 'motes' of genuine microscopic dimensions have
yet to be created. The cost of sensor nodes is similarly variable, ranging from hundreds of dollars to a few cents, depending
on the size of the sensor network and the complexity required of individual sensor nodes. Size and cost constraints on
sensor nodes result in corresponding constraints on resources such as energy, memory, computational speed and bandwidth. |
| A sensor network normally constitutes a wireless ad-hoc network, meaning that each sensor supports a multi-hop
routing algorithm. In computer science and telecommunications, wireless sensor networks are an active research area with
numerous workshops and conferences arranged each year. |
| A number of data mining algorithms have been recently developed that greatly facilitate the processing and
interpreting of large stores of data. One example is the association rule-mining algorithm. Priori algorithm is an example of
association rule mining algorithm. Using this algorithm, candidate patterns that receive sufficient support from the database
are considered for transformation into a rule. |
| One limitation of many association rule-mining algorithms such as the Apriori algorithm is that only database
entries, which exactly match the candidate patterns, may contribute to the support of the candidate pattern. This creates a
problem for databases containing many small variations between similar patterns and for databases containing missing
values. In the wireless sensor networks association rule mining techniques are used to fetch the data sensing patterns. |
RELATED WORK |
| There are a number of papers investigating how compressive sensing can be applied in WSNs. We can classify
them according to whether projections are computed “temporally” or “spatially”. The “temporal” projections are used,
where each sensor computes projections of its own data and sends it to the data fusion centre. It also discusses how fault
tolerance can be realized based on the framework discussed, where all signals are reconstructed at the data fusion centre. A
minimal number of signals have to be reconstructed to achieve computation efficiency at the data fusion centre. |
| Other works in applying compressive sensing in WSNs view the spatial data from the sensors at each time instance
as an image or snapshot, and compute projections of the sensor data for each snapshot. All these works aim at obtaining a
sufficient accurate snapshot of the sensor field by using as little energy as possible. The work [3] realizes this goal by using
an additive radio channel to compute projections. The works in [6], [10], [5] compute projections by passing messages
between sensors, while the work in [11], [9] consider random samples as projections. There is a rich literature in fault
tolerance in WSNs. The work [4] discusses the types of faults that commonly appear in WSNs. The papers [7] use a
Bayesian approach to detect whether sensors are faulty. The work [8] proposes to detect sensor faults by using recurrent
neural networks. |
| The problem of computing a robust average also appears in other fields, e.g., reputation ranking and fair
assessment of students’ work in education [2]. However, this estimator experiences convergence problem, a fact which we
also pointed out. The use of projection matrix as a dimensionality reduction method is fairly well known in the data mining
and the machine learning communities. The framework depicted opens up the possibility of using some of the algorithms
developed in these communities to WSNs, e.g., performing clustering using the compressed data. A feature of our
algorithm is that it works directly with the compressed data without decompressing them. There is also some recent effort
in using compressed data directly for classification and detection, see [12]. |
COMPRESSIVE DATA COLLECTION SCHEME |
| This paper considers the fusion of distributed compressive sensing data in a wireless sensor network (WSN).
Compressive sensing is a collection of recently proposed sampling and signal reconstruction methods. A promise of
compressive sensing is that it can obtain a good approximation of an unknown signal by performing a small number of
generalized measurements, called projections, provided that the unknown signal is compressible. For WSNs, it means that
compressive sensing can be used to reduce the bandwidth requirement and lower the energy consumption. |
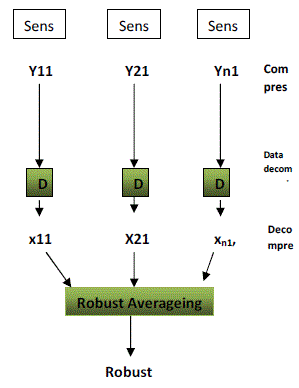
| Fig. 3.1 depicts a “standard” method in which distributed compressive sensing can be used to compute a robust
average in a WSN. Instead of sending the original sensor measurements, each sensor performs projections on its sensor
measurements to produce a lower bandwidth compressed data stream. These compressed data streams are then transmitted
over the WSN to reach the data fusion centre, where these data streams are decompressed to retrieve the original signals (or
more precisely, an accurate approximation of the original signals because the compression is lossy). Based on the
decompressed data streams, the data fusion centre can examine which of the signals are faulty. Assuming that we are
interested in calculating the average of the data, we can now use the decompressed data streams to determine suitable
weights for this averaging operation, e.g., by weighting noisy signals less than the clean signals. The key advantage of this
method is that bandwidth will be saved by sending compressed data streams over the network. |
| In this paper, we examine the alternative method depicted for this method; the sensors again send compressed data
streams to the data fusion centre. The main difference is the sequence of operations to be performed at the data fusion
centre. Instead of first decompressing the compressed data to obtain the original data stream, our proposed method will
work directly with the compressed data without decompressing them. Our proposed method determines a weight for each of
the compressed data streams, which reflects whether the sensor which produces the compressed data stream may be faulty
or not. We then apply these weights to compute a robust average of the compressed data streams. A nice property of this
robust average of the compressed data streams is that, upon decompressing (or applying the compressive sensing
reconstruction method to) this stream, we will obtain an approximation of the robust average of the original sensor
readings. The key advantage of our proposed method is a great reduction of computation requirement at the data fusion
centre. First, we work directly with the compressed data, whose dimension is only a fraction of that of the original sensor
readings. Second, we only need to perform decompression (or compressive sensing reconstruction) once, this represents a huge saving in computation requirement because each decompression requires a linear programming problem to be solved.
In addition, we show that our fusion algorithm can be implemented on resource limited wireless sensor nodes. |
SYSTEM MODELS |
Basic Models |
| We consider a WSN with n sensors indexed by s = 1, . . . , n. We assume that the sensors are time synchronized
and at each time slot t, each sensor performs a measurement. We will use xst to denote the sensor reading by sensor s at time
slot t. We assume that the network works on one block of data with m consecutive data points in a block; therefore, a block
of data consists of {xst} with s = 1, . . . , n and
t = 1, . . .,m. Note: As depicted the sensors will not send their readings xst directly to the data fusion centre to
conserve bandwidth and energy. Instead, each sensor will perform projections on its sensor readings and send only the
results of the projections, which we call either the compressed data stream or the compressed data, to the data fusion centre.
The action of, say sensor s, on projecting its data sequence xst (t = 1, . . .,m) can be expressed in matrix form, as follows: |
| The matrix Ф is the projection matrix, and the vector ys is the result of the projection. (Note that all vector and
matrix quantities are typeset in boldface in this paper.) The theory of compressive sensing says that the elements Фij can be
drawn from one of these distributions: 1) Standard Gaussian distribution; 2) Symmetric Bernoulli distribution of random
numbers {+1,-1}; or 3) Categorical distribution whose outcomes √3, 0, and -√3 occur with probability 1/6, 2/3 and and 1/6,
respectively. We assume that all the sensors use the same projection matrix for each block of data. Since the network is
synchronized, this can be achieved by using a time dependent seed for the pseudorandom number generators. This also
means that the sink knows the projection matrix that is being used, and the sensors do not have to send this information.
The parameter p (< m) here is the number of projections to be used, and we assume that all sensors use the same value of p. |
| The compressed data stream {ysk} (for k = 1, . . . , p) is to be transmitted by sensor s to the data fusion centre of the
WSN. For practical implementation, it is easier to use either Bernoulli distribution or Categorical distribution mentioned
earlier. For Bernoulli distribution, it will be easier for the sensors to send √pysk to the data fusion centre because only
integer addition and subtraction are needed to perform by the sensor nodes. Furthermore, for suitable values of p, the
transmission of the sequence {ysk} will require less number of bits than {ysk}. If the analog-to-digital (A/D) convertor on
the sensor uses b bits, then sending the original sequence will need mb bits. However, sending the compressed sequence
(assuming the aforementioned practical implementation) will require p(b + 1 +[log2 m]) bits (where [u] denote the smallest
integer larger than or equal to u) because the range of ysk is [-m(2b – 1); m(2b – 1). Thus, bandwidth is saved if p(b + 1 +
[log2 m]) < mb (assuming that no special coding scheme is used) and we will show that using data from WSN deployments.
With suitable implementation of Categorical distribution, the sensors again only have to perform integer arithmetic. Also,
sampling energy can be saved if a zero is drawn from the Categorical distribution because such samples are not needed. For
the rest of this paper, we will assume that either the Bernoulli or Categorical distribution is used. Note that we will continue
to write projection using the convention in (2), which is commonly used in compressive sensing literature but noting that
the practical implementation may be slightly different. |
Data and Fault Models for Robust Averaging |
| We assume that all the sensors in WSN are measuring the same physical value at any given time but some of the
sensors can be faulty. The type of faults can be bias, stuck-at fault or heterogeneous measurement noise [7]. We model that
by assuming that the sensor reading of sensor s at time t, xst, is generated from the Gaussian distribution with mean rt and
variance σ2
s , i.e., xst N(rt, σ2
s ). In other words, the model assumes that all sensors should have the same mean reading rt at
time t but the measurement noise of different sensors can be different. Our goal is, therefore, to recover the value of rt from
the sensor readings. We will refer to this process of recovering rt in the presence of faults as robust averaging. |
ISSUES ON COMPRESSIVE DATA COLLECTION SCHEME |
| Wireless sensor networks (WSNs) perform the data collection over a large geographic area. Computing and
tracking the spatial-average of the sensor measurements are estimated over a region of the WSN. Sensor faults and
heterogeneous measurement noise factors affects the sensor data average process. Robust averaging fixed-point iteration
algorithm is used to compute a weighted average of sensor measurements with noise and faults. Each sensor performs
projections on its sensor measurements to produce a lower bandwidth compressed data stream. Data approximation process
is used to assign relevant data values for missed or noisy data values. The sensors in the WSN use random projections to
compress the data and send the compressed data to the data fusion centre. The data fusion centre only need to perform
decompression once to compute the robust average to reducing the computational requirements. The following drawbacks
are identified in the existing system. |
| Projection prediction is not supported by the system |
| Transmission coverage factors are not considered |
| Limited projection accuracy levels |
| Scheduling schemes are not used |
SCHEDULING ENABLED COMPRESSIVE DATA COLLECTION SCHEME |
| The compressive data collection scheme is enhanced with Bayesian approach to support projection count
prediction. Sensing and transmission coverage factors are integrated in the data collection process. Data projection accuracy
is improved with frequent pattern identification mechanism. The data collection scheme is tuned to support scheduling
schemes to increase network lifetime. The sensor network data collection process is improved with optimal data projection
schemes. Energy management is integrated with the sensor data capturing process. Sensing and transmission coverage
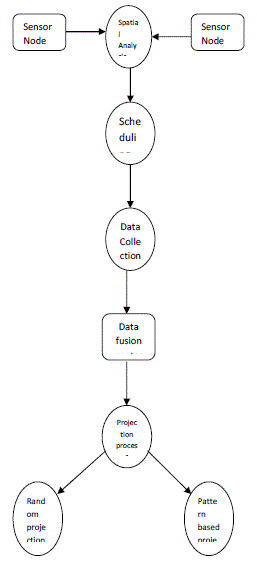
based scheduling is applied in the system. The system is divided into five major modules. They are sensor network
construction, scheduling process, data fusion center, pattern analysis and data projection process. |
| Sensor network deployment process is carried out in the network construction process. Data capturing sessions are
assigned in the scheduling process. Data fusion center is used to collect the data values from the sensor nodes. Pattern
analysis is performed to estimate the data capture patterns. Data projection process is used to estimate the missing data
elements. |
Sensor Network Construction |
| Sensor networks are constructed with node count and node type information. Sensor nodes are placed with
reference to the spatial coverage information. Sensing and transmission coverage details are used in the sensor networks.
Spatial regions and associated sensor nodes are assigned in the deployment process. |
Scheduling Process |
| Sensor node captures the environment data and updates it into the local storage. Data sensing sessions are used to
manage energy levels. Sleep-wakeup scheduling algorithm is used for ode scheduling process. Data capture and
transmission operations are carried out with scheduling details. |
Data Fusion Center |
| Data fusion center is used to collect sensor data values. Compressed data values are collected from the sensor
nodes. Compressive data values are processed to fetch the aggregated data values. Projection methods are used to fetch the
missing data values. |
Pattern Analysis |
| Pattern analysis mechanism is used to find out the data capture patterns. Frequent pattern mining is applied on
each sensor. Support and confidence levels are used to estimate frequent patterns. Apriori algorithm is used for the pattern
analysis process. |
Data Projection Process |
| Data projection process is performed under the data fusion center. Projection points are estimated using the
Bayesian approach. Random projection method is applied to estimate the missing values. Pattern based projection scheme
is applied to improve the projection accuracy levels. |
DATA COLLECTION AND WSN DEPLOYMENTS |
| We have studied the behaviour of our robust averaging algorithm when it is applied to three commonly found
sensor faults in WSNs, namely stuck-at-faults, offset, and variance degradation fault [7]. Our study shows that our robust
averaging algorithm can deal with these faults, even when a mixture of them appears in a WSNs, see Appendix C (online
supplemental material). We have applied our robust averaging algorithm to data obtained from two outdoor WSN
deployments. The results for the Belmont deployment (with 32 temperature sensors) are presented (online supplemental
material). Note that the results presented in this section are obtained from using the symmetric Bernoulli distribution to
form the projection matrix. The results from using Categorical distribution to form the projection matrix are very similar
and are not shown here. |
| This section describes the results of applying our robust averaging algorithm to the data obtained from an outdoor
WSN test bed operated by CSIRO in their QCAT research facility in Brisbane, Australia. The WSN consists of five sensors
measuring humidity and a block of data for each sensor consists of 400 points. The first four sensors have the same trend,
but the fifth sensor shows completely erroneous measurements. |
CONCLUSION |
| Wireless sensor network uses the data fusion centers to collect and process data values from sensor nodes.
Compressive data collection methods are used to handle data collection under faulty and noisy environment. Data collection
scheme is improved with Bayesian approach to predict projections. Scheduling schemes are integrated with the system to
increase the network lifetime. The system achieves high computational efficiency. Communication load is reduced by the
compressive data collection scheme. Efficient fault and noise handling mechanism is provided in the sensor data collection
process. Data collection accuracy is improved in the pattern based model. |
| |
Figures at a glance |
 |
 |
| Figure 1 |
Figure 2 |
|
| |
References |
- Chun Tung Chou, AleksandarIgnjatovic, and Wen Hu, “Efficient Computation of Robust Average of Compressive Sensing Data in Wireless Sensor Networks in the Presence of Sensor Faults” IEEE Transactions on Parallel and Distributed Systems, Vol. 24, No. 8, August 2013.
- Ignjatovic, C.T. Lee, P. Compton, C. Cutay, and H. Guo, “Computing Marks from Multiple Assessors using Adaptive Averaging,” Proc. Int’l Conf. Eng. Education (ICEE), 2009.
- W. Bajwa, J. Haupt, A. Sayeed, and R. Nowak, “Joint Source-Channel Communication for Distributed Estimation in Sensor Networks,” IEEE Trans. Information Theory, vol. 53, no. 10, pp. 3629-3653, Oct. 2007.
- K. Ni, N. Ramanathan, M. Chehade, L. Balzano, S. Nair, S. Zahedi, E. Kohler, G. Pottie, M. Hansen, and M. Srivastava, “Sensor Network Data Fault Types,” Trans. Sensor Networks, vol. 5, no. 3, article 25, May 2009.
- C. Luo, F. Wu, J. Sun, and C. Chen, “Compressive Data Gathering for Large-Scale Wireless Sensor Networks,” Proc. ACM Mobicom ’09, Sept. 2009.
- S. Lee, S. Pattem, and M. Sathiamoorthy, “Spatially-Localized Compressed Sensing and Routing in Multi-Hop Sensor Networks,” Proc. Third Int’l Conf. Geosensor Networks (GSN), 2009.
- S. Ganeriwal, L. Balzano, and M. Srivastava, “Reputation-Based Framework for High Integrity Sensor Networks,” Trans. Sensor Networks, vol. 4, no.3, article 15, May 2008.
- O. Obst, “Poster Abstract: Distributed Fault Detection Using a Recurrent Neural Network,” Proc. Int’l Conf. Information Processing in SensorNetworks (IPSN ’09), pp. 373-374, 2009.
- R.K. Rana, C.T. Chou, S.S. Kanhere, N. Bulusu, and W. Hu, “Ear-Phone: An End-to-End Participatory Urban Noise Mapping System,” Proc.ACM/IEEE Ninth Int’l Conf. Information Processing in Sensor Networks (IPSN ’10), Apr. 2010.
- C.T. Chou, R. Rana, and W. Hu, “Energy Efficient Information Collection in Wireless Sensor Networks Using Adaptive Compressive Sensing,” Proc IEEE 34th Conf. Local Computer Networks (LCN ’09), 2009.
|