ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
T. Satyendra kumar1, C.Vijaya Rani2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
The information published in the social networks need to be elegant and more individualized. By recognizing this in social networks motivated us, to propose a scheme called privacy protection scheme which prevents the revelation of identities of both users and some selected features in their profiles. Each user can pick out the features of his own profile he wishes to hide. In this report, we simulate the users as nodes and the feature as labels in the social networks which are modeled as a graph .Labels in the graph are treated as sensitive or non-sensitive. The background knowledge held by the rivals and sensitive data or information that needed to be protected are considered or treated as node labels. We allow the graph data to be published in such a way that the rival who holds the information about node’s neighborhood cannot safely infer it’s both identity and its sensitive labels by presenting a privacy protection algorithm. This algorithm transforms the nodes in original graph as amply identical. The designed algorithm may lose little information but preserves its usefulness as much as it can. The original graph structure and its properties are also evaluated to find which extent the algorithms preserve privacy. We also demonstrated that the solution we proposed is effective, efficient and scalable than those in anterior research.
I. INTRODUCTION |
| The data published in the social networks need to be protected since there is a threat to the sensitive information about users. Though many privacy models where proposed, they only prevented the accidental leakage of personal information and attacks by spiteful persons. The previous models are only concerned with link revelation and identity of users. In this report, we simulate the users as nodes and the feature as labels in the social networks which are modeled as a graph .The structural properties of the graphs are considered as protection mechanisms and threat definitions. The information published in the social networks need to be elegant and more individualized. By recognizing this in social networks motivated us, to propose a scheme called privacy protection scheme which prevents the revelation of identities of both users and some selected features in their profiles. |
| The personal information like name, age, mobile number, and current location of users are given to the social networks like Twitter and facebook. The details and messages are considered as features of their profiles. The privacy protection scheme which we proposed prevents the revelation of identities of both users and some selected features in their profiles. Each user can pick out the features of his own profile he wishes to hide. |
| We simulated the users as nodes and the features as labels in the social network which are modeled as a graph. Labels in the graph are treated as sensitive or non-sensitive. Figure 1 shows the small subset of social network. Nodes in the graph represents as users and the edges in the graph represents the information about that the two users are friends. The location of the nodes is represented by annotating the labels with first letter of city name. A few users feel free in publication of their residence in Social networks, but few people mind due to their own reasons. Because of this reason the data publication need to be protected to provide privacy of such users. Thus we consider the locations as either sensitive or non-sensitive. In the figure 1 the labels annotated with red italic letter are sensitive and remaining are nonsensitive. |
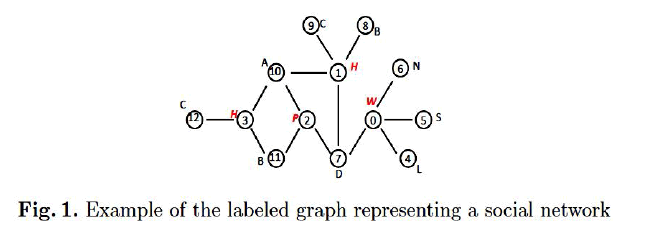 |
| The disclosure of sensitive lables arises a privacy issue and those labels are suggested by someone to delete may cause incomplete view of the social network. This may hide some exciting statistical data which doesn’t make threats to the privacy of user. In our approach we are going to release the information of sensitive labels in the same way we protect the identities of users from privacy issue. Such threats are considered as neighborhood attacks where the rivals have earlier knowledge about the intended user no. of neighbours and their labels. In this paper we propose an algorithm in such a way the rival cannot know about the identity and sensitive labels of the users. By considering the situation that the rival has already know the information about the neighborhood details and sensitive labels. |
| The Privacy protection algorithm we presented will make over original graph into a graph in such a way that each node having sensitive label may be identical with at least l - 1 remaining nodes. The possibility to assume to have is considered as not more than 1/l. To overcome this problem we designed l -diversity-like model; in which node labels are treated as that the rival has already know the information about the neighborhood details and sensitive labels which has to be protected. |
II PROBLEM DESCRIPTION |
| The social network is modeled as G(V,E,Ls; L,I’), where V is a set of nodes, E is s set of edges, LS is a set of sensitive labels, and L is a set of non-sensitive labels. ÃÂó maps nodes to their labels, ÃÂó : V -> LS U L. Then, we designed l - diversity-like model; in which node labels are treated as that the rival has already know the information about the neighborhood details and sensitive labels which has to be protected. The definitions 1 and 2 given below will clarify the concepts about neighborhood information and sensitive label information respectively. |
Definitions: |
| 1)The degree and labels of υ’s is considered as neighborhood information in our approach. |
| 2) Each node having sensitive label may be identical with at least l - 1 remaining nodes is our l -sensitive-labeldiversity. |
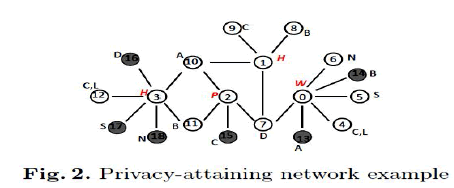 |
| The above graph is in 2-sensitive-label-diversity;since 0 and 3 nodes are identical have neighbors with labels A, B, {C,L}, D, S, N alone ,in the same way the nodes 1 and 2 have identical neighbors A, B, C, D alone. |
III ALGORITHM |
| The intention of our proposed algorithm is to give assurance of the l-sensitive-label-diversity requisites. To achieve this we assemblage the appropriate nodes and make necessary changes to the labels of neighbor nodes of each group.We assemblage the nodes having identical neighbor labels in such a way to make new few labels and add few noise nodes to it.As we know that the previous DNN and INN algorithms will reduce the resemblance calculation of neighbor nodes .The detailed information about DNN and INN algorithms refer to [3].To overcome these difficulties with previous algorithms, we propose a new algorithm Global-similarity-based Indirect Noise Node (GINN). |
GINN Algorithm |
| The first of algorithm starts with, the nodes which have not yet grouped is grouped into a cluster like form. If the two nodes have maximum similarity of neighborhood labels then those nodes are grouped as one in the first run. Since the neighbor labels are identical to the both nodes then those labels are changed to one. For two nodes, v1 and v2 with neighborhood label sets (LSv1) and (LSv2 ) respectively, we calculate neighborhood label similarity (NLS) as follows: |
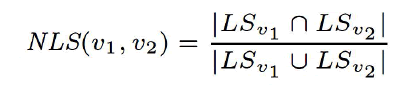 |
| The two neighborhoods are said to have larger similarity, if the value of NLS is large. |
| The nodes having maximum similarity of neighborhood labels then those nodes are grouped as one cluster until the group has l nodes with different sensitive labels. Thereafter, the algorithm proceeds to create the next group. If less than l nodes are remained subsequent to the last group's creation, these remainder nodes are clustered into existing groups according to the similarities between nodes and groups. |
| Now the all the nodes in the group will have identical neighborhood labels. We have three modification operations to ensure low losses of information in our graph.They are: label union, edge insertion and noise node addition. |
 |
| -sensitive-label-diversity is satisfied by every node in the each group by noise node operation in our algorithm. Only after all the groundwork grouping operations are performed, the algorithm proceeds to process the expected node addition operation at the final step. Afterward, if two nodes are expected to have the same labels of neighbors and are within two clusters, no more than one node is added. In other words, we combine some noisy nodes with the same label, thus resulting in fewer noisy nodes. |
IV EXPERIMENTAL EVALUATION |
| Utilizing synthetic and real data sets our approach is evaluated. We implement all our approaches in python. We conduct our experiments on an Intel core, 2Quad CPU, 2:83GHz machine with 4GB of main memory running Windows 7 Operating System. Three data sets are used in our approach. The network hyperlinks b/w weblogs on US politics is our first data set .The facebook data set generated is considered as our second data set. A family of synthetic graphs with unstable no. of nodes is our third data set. For the evaluation of data effectiveness and information loss we use first and second data sets. To measure running time we use third data set. |
Data effectiveness |
| By the analysis of dimensions on degree distribution, label distribution, degree centrality, clustering coefficient, average path length, graph density, and radius we compare the data effectiveness. We demonstrate the number of the noisy nodes and edges required for each advance. |
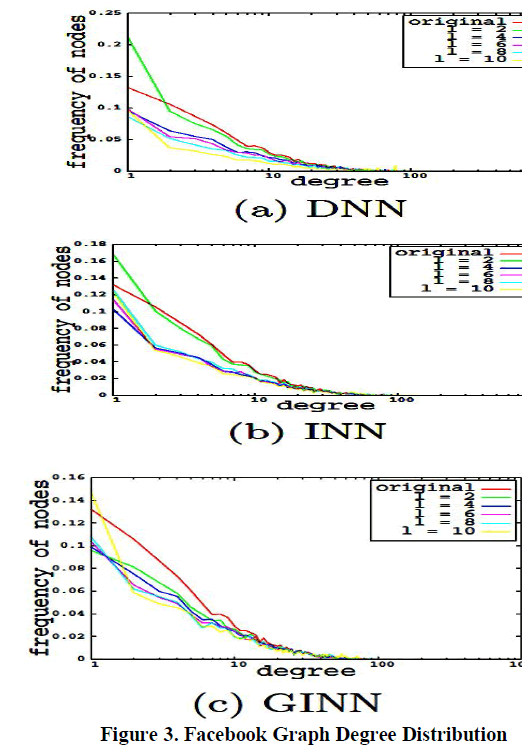 |
| Both ahead and later modification of degree distribution of the Facebook graph is depicted in figure 3. In figure 3 the subfigure (a) depicts the degree distributions of graphs by DNN algorithm. Similarly, the subfigure (b) and (c) depicts the degree distributions of graphs by INN and GINN algorithms respectively. When l is small the degree of distribution in original and modified graphs look like same. The measurements of these graphs are clearly explained in reference [3].To achieve privacy limitation our GINN algorithm maintain graph properties well when compared with DNN and INN algorithms. |
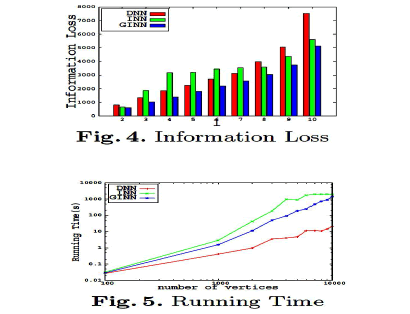
Information Loss |
| Our intent is to remain information loss low in analysis of effectiveness. Both structure and label information loss comes under this information loss .To determine the loss we followed like this: for every node |
 |
 |
Algorithm Scalability |
| In Figure 5,we represented the running time of DNN,INN and GINN algorithms as the number of nodes increases. We found the algorithm DNN is faster when compared with INN and GINN algorithms.DNN showed a good scalability at the cost when large noisy nodes are added. Our proposed GINN algorithm can also be used for reasonably large graphs in the following way: 1) We separate the nodes into two different categories, with or without sensitive labels. 2) Such smaller granularity reduces the number of nodes the anonymization method needs to process, and therefore improves the overall effectiveness. |
V. CONCLUSION |
| The personal data published in the social networks is protected and investigated in this paper. The graphs with rich label information is categorized as either sensitive or non-sensitive. To infer the sensitive labels of targets the rivals use the prior knowledge about node’s degree and labels of its neighbors. Both rivals background knowledge and sensitive information of node labels take part in attaining privacy while publishing the data through our model. To limit rivals confidence about sensitive label data, in our approach the model is accompanied with algorithms that transform a network graph before publication. We guaranteed a clear privacy with experiments on real and synthetic data sets which bear out the scalability, effectiveness and efficiency. In our approach we also maintain critical graph properties to provide guaranteed privacy. |
References |
|