International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Selection of Optimal Mother Wavelet for Fault Detection Using Discrete Wavelet Transform

Dr. Bhola Jha1, R. B. Yadav2, Dr. K. R. M Rao3 and H. L. Yadav4
  1. Asst. Prof., Dept. of Electrical Engg., G. B. Pant Engg. College, Pauri-Garhwal-246194, India
  2. Asst. Prof., Dept. of Electrical Engg., G. B. Pant Engg. College, Pauri-Garhwal-246194, India
  3. Professor, Dept. of Electrical Engg., M. J College of Engg.&Technology, Hyderabad-500034, India
  4. Asst. Prof., Dept. of Civil Engg., G. B. Pant Engg. College, Pauri-Garhwal-246194, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper exploited the various mother wavelets for fault detection. A different value of fault resistances analyzed on different types of mother wavelets. Comparisons are made based on the sum of coefficients in multi resolution signal decomposition (MSD) using Discrete Wavelet Transform (DWT). Based on the extensive investigations on different value of fault resistance in Line-Ground (L-G) fault, optimal mother wavelet is proposed.

Keywords
Wavelet, wavelet coefficient, fault, multi resolution decomposition

INTRODUCTION
Recently wavelet applications are extended to electrical engineering field especially in terms of faults detection and discrimination. An internationally recognized tool wavelet analyzed from theory point of view that it can be formulated via a family of basis functions such that the signals can be described in a localized time and frequency format. Hence, by employing the long windows at low frequency and short windows at high frequencies, the wavelet transform will be capable of comprehending the time and frequency information simultaneously. For those transients in time-varying signals, they would be supervised more effectively, thereby encouraging the application of such method to enhance the detection capabilities.
In the area of fault detection capability, still limited numbers of wavelet-based research papers are reported [1-5]. CWTbased approach is proposed in [1] for the enhancement of damage detection of wind turbine blades. Wavelet-based ARMA model is presented in [2] for the short-term wind speed forecasting. Comparative analysis of the approaches, MCSA, EPVA and DWT are made in [3] to detect the interturn fault in Doubly-Fed Induction Generator (DFIG). Based on Discrete Wavelet Transform (DWT), Fault Indicator and Fault Criteria, Detection of High Impedance Fault (HIF) is proposed in [4]. A solution to the problem of protecting aerial lines from high impedance fault in distribution systems is proposed in [5]. Transmission line faulty phase analysis is done in [6] by detailed coefficients. Based on the energy of differential-current signal, transformer fault’s detection is proposed in [7]. Magnetizing in-rush current and fault current of transformer is discriminated in [8]. A new diagnostic method based on grid modulating signals is proposed in [9] to detect asymmetrical fault. Coefficients of wavelet used as a input for training back propagation neural network in high impedance fault detection is analyzed in [10]. Technique based on sensitive fault detection parameter from multi resolution decomposition of three phase currents is proposed in [11]. However, each of the paper improves fault detection capabilities to certain extent, but each has its drawbacks as well. In those papers authors have used different mother wavelets, but they did not predict the optimal mother wavelet which actually affects the accuracy of detection capabilities. In this paper, comparisons are made among different mother wavelet, based on the sum of coefficients in multi resolution signal decomposition (MSD) using Discrete Wavelet Transform (DWT). After the extensive investigations on different value of fault resistance, an optimal mother wavelet is proposed for the accurate fault detection.

WAVELET TRANSFORM
Wavelet transform is of two types Discrete Wavelet Transform (DWT) and Continuous Wavelet Transform (CWT). Their brief explanations are as under.
Discrete Wavelet Transform (DWT)
The ability to provide variable time-frequency resolution is hallmarks of wavelet transform [12-14]. Wavelet transform is relatively new mathematical technique which is used to analyze signal in nature. It is becoming the focus point of much science, and is fondly delighted tool by scientists. It plays a very important role in signal and information processing. The wavelet transformation is processes of determining how well a series of wavelet functions represent the signal being analyzed. The goodness of fitting of the function to the signal is described by the wavelet coefficients. The result is a bank of coefficients associated with two independent variables, dilation and translation. Translation typically represents time, while scale is a way of viewing the frequency content. Larger scale corresponds to lower frequency meaning thereby better resolution. The most efficient and compact form of the wavelet analysis is accomplished by the decomposing a signal into a subset of translated and dilated parent wavelets, where these various scales and shifts in the parent wavelet are related based on powers of two. Full representation of a signal can be achieved using a vector coefficients the same length as the original signal.
image
The number of coefficients necessary to describe the signal may be larger than the signal strength, as the CWT over samples the signal.
Characteristics of Wavelets
The quality of various wavelet families vary according to the following criteria
• The speed of convergence to zero
• The number of vanishing moments
• The symmetry
• The regularity
• The othogonality/biorthogonality
• The existence of scaling function
The comparision of four mother wavelets are tabulated based on the qualities mentioned above. From this table it is found that the accuracy of Coiflets wavelet is better than remaining three.
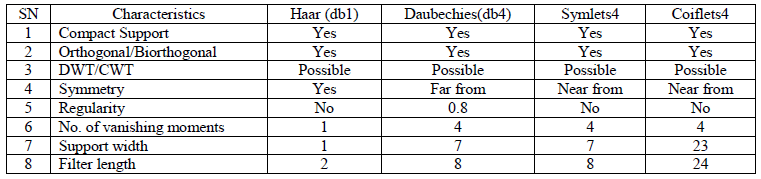image
Case Study
To validate the accuracy of Coiflets mother wavelet is better, a case study is done on the following test system which is shown in Fig.1.
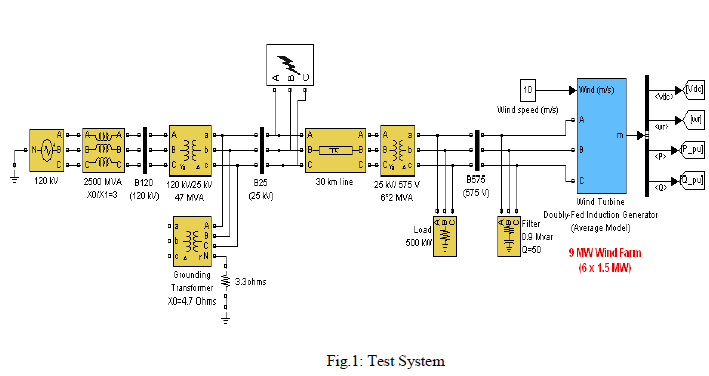image
A 9MW Doubly Fed Induction Generator-Based Wind Turbine is connected to 120kV grid through transformers and transmission lines. Single Line-Ground (L-G) fault is created on 25kV bus transmission lines which is shown in test system of Fig.1.

RESULTS ANALYSIS
The sum of coefficients of currents signals using different mother wavelet for different values of fault resistances are shown in Fig.2, Fig.3, Fig.4 and Fig.5. The coefficients are obtained through multi resolution decomposition using one dimensional discrete wavelet wavelet transform.
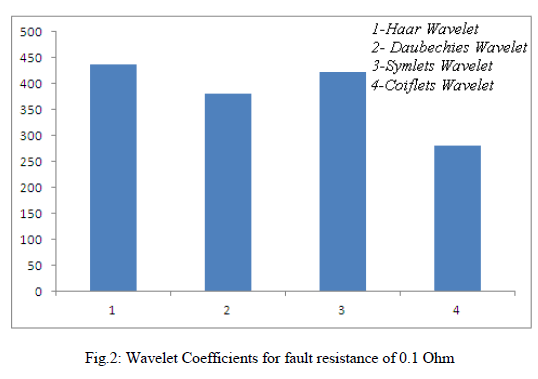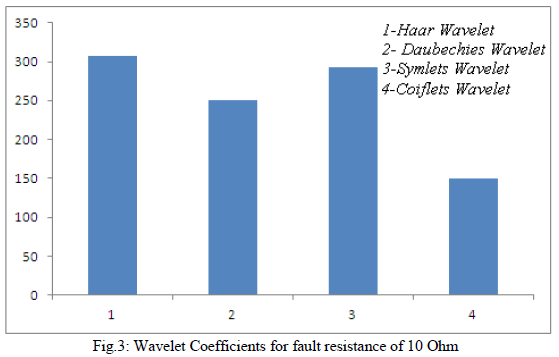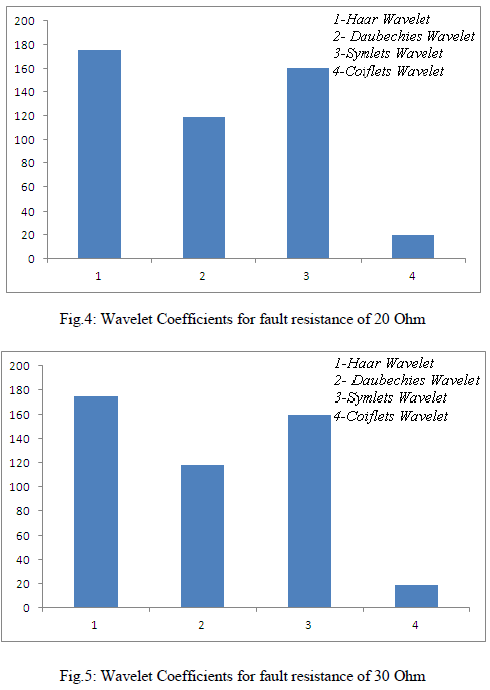image
image
image
This is found from the bar chart that the the sum of coefficients of Coiflets wavelet is less for all values of fault resistances. Hence, Coiflets is an optimal mother wavelet for fault detection.

CONCLUSION
Based on the extensive investigations on different value of fault resistance, Coiflets wavelet is proposed as an optimal mother wavelet.

References
  1. Chin-Shun Tsai, Cheng-Tao Hsieh, and Shyh-Jier Huang “ Enhancement of Damage-Detection of Wind Turbine Blades Via CWT-Based Approaches” IEEE transactions on Energy Con version, Vol. 21, No. 3, pp 776-781, Sept. 2006..
  2. CAO Lei and LI ran “Short-Term Wind Speed Forecasting Model for Wind Farm Based on Wavelet Decomposition” DRPT, 6-9 April, Nanjing China. pp 2525-2529, 2008.
  3. H. Douglas, P. Pillay and P. Barense “ The Detection of Interturn Stator Faults in Doubly-Fed Induction Generators” IEEE, IAS, pp 1097-1102, 2005.
  4. Chul-Hwan Kim et. al. “A Novel Fault Detection Technique of High Impedance Arcing Faults in Transmission Lines Using the wavelet Transform” IEEE Transactions on Power Delivery, Vol.17, No.4, pp 921-929, Oct.2002.
  5. Miing-Ta Yang, Jin-Lung Guan and Jhy-Cherng Gu “High Impedance Faults Detection Technique Based on Wavelet Transform” World Academy of Science, Engg. and Technology, pp 308-312 , 2007.
  6. B. Ravindhraratnath Reddy et.al. “Detection and Localization of Fault in Transmission Line Using Wavelet Transform” Journal of Theoritical and Applied Information Technology, pp.99-104, 2009.
  7. Y. Ngafi Sarem, E. Hasemzadeh and M.A.Layegh “Transformer Fault Detection Using Wavelet Transform” International Journal on Technical and Physical Problems of Engg., Vo.4, No.1, Issue 10, pp17-26, March 2012.
  8. Okan Ozgonenel, Giiven Onbligein and Gagri Kocaman “Transformer Protection Using Wavelet Transform” Turk. J. Elect. Engin.,Vol13(1), 2005.
  9. R. K. Dubey “A Novel Technique for Asymmetrical Fault Detection in DFIG-Based Wind Farm” Bulletin of Electrical Engg. and Informatics, vo.1, No.4, pp.285-295, Dec.2012.
  10. Abdulhamid et.al. “Hybrid Algorithm for Detection of High Impedance Arcing Fault in Overhead Transmission Systems” International Journal of Electronic and Electrical Engg., Vol.2, Isuue4, May 2012.
  11. N. Zamanan, M. Gilany and W. Wahba “A Sensitive Wavelet-Based Algorithm for Fault Detection in Power Distribution Network” ACEEE Inernational Journal on Communication, Vol.2, No.1, pp.46-50, March 2011,.
  12. “Wavelet Transforms” by Rghuveer. M. Rao and Ajit. S. Bopardikar Pearson Education, Low Price Edition, 2005.
  13. Wavelet Tutorial Vol. I, II, III by Robi Polikar.
  14. www.mathworks.com