ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
C.Selvarathi1, M.E, K.Karthika2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
Clustering is one of the most important techniques in machine learning and data mining tasks. Similar data grouping is performed using clustering techniques. Similarity measures are used to estimate transaction relationships. Hierarchical clustering model produces the results like tree structured. Partitioned clustering produces results in the grid format. Text documents are unstructured values with high dimensional attributes. Document clustering group up unlabeled text documents into the meaningful clusters. Traditional clustering methods require cluster count (K) for the document grouping process. Clustering accuracy degrades highly with reference to the unsuitable cluster count. Document features are automatically divided into two groups’ discriminative words and non discriminative words. Only discriminative words are needful for grouping documents. Discriminative word identification process is improved with the labeled document analysis mechanism. Concept relationships are analyzed with Ontology support. The system improves the scalability with the support of labels and concept relations for dimensionality reduction process.
INTRODUCTION |
| Clustering is the classification of objects into different groups, or more precisely, the partitioning of a data set into subsets, so that the data in each subset share some common trait - to some defined distance measure. Data clustering is a common technique for statistical data analysis, which is used in many fields, including machine learning, data mining, image analysis and bioinformatics. Besides the term data clustering, there are a number of terms with similar meanings, including cluster analysis, automatic classification, numerical taxonomy, botryology and typological analysis. |
| Clustering refers the operation of grouping the transactions with reference to the similarity values. The text documents are referred as unstructured databases. The text documents may not be produced as fixed length or fixed structure data values. The text documents are produced as raw data collections. The text document is preprocessed for the clustering process. The text document clustering requires the document elements as a collection. The terms in a text documents are represented as a term document matrix. The term matrix collection is used for the clustering process. The term weight values are used for the similarity measurement estimation. Those are carried out in the preprocessing. The stop word elimination and stemming operations. The text document clustering refers the clustering of term matrix of a document. |
RELATED WORK |
| Document clustering methods can be categorized based on whether the number of clusters is required as the input parameter. If the number of clusters is predefined, many algorithms based on the probabilistic finite mixture model have been provided in the literature. Nigam et al. proposed a multinomial mixture model. It applies the EM algorithm for document clustering assuming that document topics follow multinomial distribution. Deterministic annealing procedures are proposed to allow this algorithm to find better local optima of the likelihood function. Though multinomial distribution is often used to model text document, it fails to account for the burstiness phenomenon that if a word occurs once in a document, it is likely to occur repeatedly. Madsen et al. [2] used the DCM model to capture burstiness well. Its experiments showed that the performance of DCM was comparable to that obtained with multiple heuristic changes to the multinomial model. However, DCM model lacks intuitiveness and the parameters in that model cannot be estimated quickly. Elkan [1] derived the EDCM distribution which belongs to the exponential family. It is a good approximation to the DCM distribution. The EM algorithm with the EDCM distributions is much faster than the corresponding algorithm with DCM distributions proposed in [2]. It also attains high clustering accuracy. In recent years, EM algorithm with EDCM distribution is the most competitive algorithm for document clustering if the number of clusters is predefined. |
| If the number of clusters K is unknown before the clustering process, one solution is to estimate K first and use this estimation as the input parameter for those document clustering algorithms requiring K predefined. Many methods have been introduced to find an estimation of K. The most straightforward method is the likelihood crossvalidation technique, which trains the model with different values of K and picks the one with the highest likelihood on some held-out data. Another method is to assign a prior to K and then calculate the posterior distribution of K to determine its value. In the literature, there are also many information criteria proposed to choose K, e.g., Minimum Description Length (MDL), Minimum Message Length (MML), Akaike Information Criterion (AIC), and Bayesian Information Criteria (BIC). The basic idea of all these criteria is to penalize complicated models (i.e., models with large K) in order to come up with an appropriate K to tradeoff data likelihood and model complexity. |
| An alternative solution is to use the DPM model which infers the number of clusters and the latent clustering structure simultaneously. The number of clusters is determined in the clustering process rather than preestimated. In our preliminary work, we proposed the DPMFS approach [3] using the DPM model to model the documents. A Gibbs Sampling algorithm was provided to infer the cluster structure. However, as the other MCMC methods, the Gibbs sampling method for the DPMFS model is slow to converge and its convergence is difficult to diagnose. Furthermore, it’s difficult for us to develop effective variational inference method for the DPMFS model. Our proposed new model and the associated variational inference method in this paper solves these problems successfully. |
DIRICHLET PROCESS MIXTURE MODEL FOR DOCUMENT CLUSTERING |
| Document clustering, grouping unlabeled text documents into meaningful clusters, is of substantial interest in many applications. One assumption, taken by traditional document clustering approaches, as in [1], [2], is that the number of clusters K is known before the process of document clustering. K is regarded as a predefined parameter determined by users. However, in reality, determining the appropriate value of K is a difficult problem. First, given a set of documents, users have to browse the whole document collection in order to estimate K. This is not only time consuming but also unrealistic especially when dealing with large document data sets. Furthermore, an improper estimation of K might easily mislead the clustering process. Clustering accuracy degrades drastically if a bigger or a smaller number of clusters is used. Therefore, it is very useful if a document clustering approach could be designed relaxing the assumption of the predefined K. |
| In this paper, we attempt to group documents into an optimal number of clusters while the number of clusters K is discovered automatically. The first contribution of our approach is to develop a Dirichlet Process Mixture (DPM) model to partition documents. The DPM model has been studied in nonparametric Bayesian for a long time [5]. It shows promising results for the clustering problem when the number of clusters is unknown. The basic idea of DPM model is to jointly consider both the data likelihood and the clustering property of the Dirichlet Process (DP) prior that data points are more likely to be related to popular and large clusters. When a new data point arrives, it either rises from existing cluster or starts a new cluster. This flexibility of the DPM model makes it particularly promising for document clustering. However, in the literature, there is little work investigating DPM model for document clustering due to the high-dimensional representation of text documents. In the problem of document clustering, each document is represented by a large amount of words including discriminative words and nondiscriminative words. Only discriminative words are useful for grouping documents. The involvement of nondiscriminative words confuses the clustering process and leads to poor clustering solution in return [7]. When the number of clusters is unknown, the affect of nondiscriminative words is aggravated. |
| The second contribution of our approach is to address this issue and design a DPM model to tackle the problem of document clustering. A novel model, namely DPMFP, is investigated which extends the traditional DPM model by conducting feature partition. Words in documents set are partitioned into two groups, in particular, discriminative words and nondiscriminative words. Each document is regarded as a mixture of two components. The first component, discriminative words are generated from the specific cluster to which document belongs. The second component, nondiscriminative words, are generated from a general background shared by all documents. Only discriminative words are used to infer the latent cluster structure. |
| The computational cost of DPM parameter estimation is also a problem for developing the DPM model for the document clustering problem. Traditionally, there are two algorithms to infer DPM parameters, in particular, the variational inference algorithm and the Gibbs sampling algorithm. It is hard to apply the Gibbs sampling algorithm to document clustering since it needs long time to converge. Due to the high-dimensional representation of text documents, it is even harder to be applied when the document data set is large. For the algorithm of variational inference, it could be applied to infer the document collection structure in a much quicker manner. However, in our DPMFP approach, we need to infer the document collection structure as well as the partition of document words at the same time. Therefore, traditional variation inference algorithm for the DPM model cannot be directly applied to our problem [8]. The third contribution of our approach is to design a method to estimate the document collection structure for the DPMFP model. A Dirichlet Multinomial Allocation (DMA) model, namely DMAFP, is used to approximate the DPMFP model to simplify the process of parameter estimation. A variational inference algorithm is then derived for the DMAFP model. The Gibbs sampling algorithm is also investigated for comparison. |
| We have conducted extensive experiments on our proposed approach by using both synthetic and realistic data sets. We also compared our approach with state-of-theart model-based clustering algorithms [1]. Experimental results show that our proposed approach is robust and effective for document clustering. |
3.1 Dirichlet Process Mixture Model |
| The DPM model is a flexible mixture model in which the number of mixture components grows as new data are observed. It is one kind of countably infinite mixture model [4]. We introduce this infinite mixture model by first describing the simple finite mixture model. In the finite mixture model, each data point is drawn from one of K fixed unknown distributions. For example, the multinomial mixture model for document clustering assumes that each document xd is drawn from one of K multinomial distributions. Let ηd be the parameter of the distribution from which the document xd is generated. Since the number of clusters is always unknown, to allow it to grow with data, we assume that the data point xd follows a general mixture model in which ηd is generated from a distribution G. The conditional hierarchical relationships are as follows: |
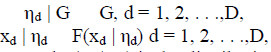 |
| where D is the number of data points and F(xd | ηd) is the distribution of xd given ηd. |
| The probability distribution G mentioned above is always unknown. If G is a discrete distribution on a finite set of values, this generative mixture model reduces to the finite mixture model. In the nonparametric Bayesian analysis, the Dirichlet process mixture model places a Dirichlet process prior on the unknown distribution G. In this way, G can be considered as a mixture distribution with a random number of components. More formally, the hierarchical Bayesian specification of the DPM model is as follows: |
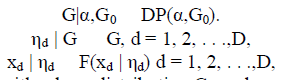 |
| where DP(α,G0) represents a DP with a base distribution G0 and a positive scaling parameter α. Intuitively, G0 is the mean of the DP and α is the inverse variance. G is more similar with G0 when a larger value is assigned to α. Since G is viewed as a random probability distribution in the DPM model, integrating out G, the joint distribution of the collection of variables η1 , η2, . . . , ηd exhibits a clustering effect. Let η-d denote the set of ηj for j ≠ d. Conditioning on η-d, the distribution of ηd has the following form: |
| Let , , . . . , denote the distinct values of η1 , η2, . . . , ηd. Let mi be the number of times that occurs in η-d. The conditional distribution of ηd given η-d follows the Po’lya urn distribution as follows: |
| Equation (2) indicates that the data point xd is either allocated to an existing cluster or a new cluster. In particular, xd can be assigned to an existing cluster with the probability proportional to the cluster size or a new cluster with probability proportional to α. The number of clusters is determined automatically. We can best understand this clustering property by a famous metaphor known as the Chinese restaurant process [4]. The hierarchical representation of the DPM model. |
| Denote z-d as the set of all zj for j ≠ d. Integrating out the mixing proportions P, we can write the conditional distribution of zd given z-d as follows: |
| where i indicates each mixture component ranging from 1 to N and nd,i,is the number of times that the value of zj equals to i for j ≠ d. If we take N → α in (3), it is easy to found that the clustering property of the DMA model is the same as that of the DPM model as shown in (2). In [5], it shows that we can choose a reasonable N based on the L1 distance between the Bayesian marginal density of the data under the DMA model and the DPM model. |
| 3.2. Mean Field Variational Inference |
| Mean field variational inference is a particular class of variational methods [6]. Consider a model with a hyperparameter θ, latent variables W = {v1, v2, . . . ,vS}, and data points x = {x1, x2, . . . , xD}. In many situations, the posterior distribution p(W|x,θ) is not available in a closed form. The mean field method approximates the posterior distribution p(W|x,θ) with a simplified distribution. It starts from a family of distributions Q by using which both the mean field procedure and the subsequent inference procedures are easy to handle. The mean field approximation q is then learned by minimizing the Kullback-Leibler (KL) divergence between the distribution in Q and p(W|x,θ) as follow: |
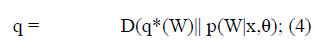 |
| where |
| D(q*(W)||p(W |x, θ)) = Eq*[log q* (W)] - E q* [logp(w,x|θ)]+log p(x|θ): |
| Note that since log p(x|θ) does not depend on the distribution q*(W), the minimization of the KL divergence can be cast alternatively as the maximization of a lower bound on the log marginal likelihood as follows: |
| log p(x|θ) ≥ E q* [logp(w,x|θ)] - Eq*[log q* (W)] (5) |
| In order to yield a computationally effective inference method, it’s very necessary and important to choose a reasonable family of distributions Q. A common and practical method to construct such a family often breaks some of the dependencies between the latent variables. In this paper, we use the fully factorized variational distributions which break all of the dependencies between latent variables. |
ISSUES ON DPM BASED DOCUMENT CLUSTERING |
| Document features are automatically partitioned into two groups discriminative words and nondiscriminative words. Only discriminative words are useful for grouping documents. The involvement of nondiscriminative words confuses the clustering process and leads to poor clustering solution in return. A variation inference algorithm is used to infer the document collection structure and partition of document words at the same time. Dirichlet Process Mixture (DPM) model is used to partition documents. DPM clustering model uses both the data likelihood and the clustering property of the Dirichlet Process (DP). Dirichlet Process Mixture Model for Feature Partition (DPMFP) is used to discover the latent cluster structure based on the DPM model. DPMFP clustering is performed without requiring the number of clusters as input. The following drawbacks are identified from the existing system. |
| Discriminative words set identification is not optimized |
| Labeled documents are not considered |
| Clustering with low scalability |
DPMFP AND DMAFP APPROXIMATION |
| Formally, we define the following terms: |
| A word w is an item from a vocabulary indexed by {1, 2, . . .,W}. |
| A cluster is characterized by a multinomial distribution over words. It is represented by a multinomial parameter. |
| A document x is represented as a W-dimensional vector xd = { xd1, xd2, . . . , xdw } where xdj is the number of appearance of the word wj of the document xd. |
| A document data set X is a collection of D documents denoted by X = {x1, x2, . . . , xD}. |
| We introduce a latent binary vector γ = { γ1, γ2, . . . , γW} to partition document features into two groups, in particular, the discriminative words and nondiscriminative words. Let Ω denote the discriminative word set. Words not belong to Ω are regarded as nondiscriminative words. For each j = 1, 2, . . .,W, we denote |
| We assign a prior to γ and assume that its elements are independent Bernoulli random variables with common probability distribution B(1, ω). The parameter ω can be regarded as the prior probability of each word in the vocabulary which is expected to be discriminative. |
| Our model assumes the generative process for the document data set X. G0 is a Dirichlet distribution with parameter = ( 1, 2, . . . , W); |xd| is the total appearance of the words in the document xd; the multinomial parameter ηd represents the specific cluster to which the document xd belongs; the multinomial parameter η0 represents the general background sharing by all the documents in the document data set X; xdγ and xd (1-γ) represent ( xd1γ1,. . . , xdWγw) and (xd1 (1 - γ1), . . . , xdw (1-γW)), respectively; |xd|1-γ, which equals to xdj , is the number of discriminative words in the document xd; |xd|1-γ, which equals to xdj , is the number of the nondiscriminative words in xd. In our model, the DP prior is only used for the specific cluster ηd. Note that |xd| is an ancillary variable as it is independent of all the other data generating parameters. Therefore, we ignore its randomness in the following development. The graphical representation of the DPMFP model. We assume that there is no correlation between the set of discriminative words and the set of nondiscriminative words. The conditional probability density function for xd is given as follows: |
| However, since the vocabulary size W is always very large, the law of large numbers and the fact that (ηdj γj + γ, η0,j (1- γj) = 1 indicate that |
| Therefore, we can approximately consider the conditional probability distribution of xd as a Multinomial distribution with parameters { ηdj γj + η0,j (1- γj),j = 1,2, . . .,W}. The approximated probability density function is as follows: |
| Furthermore, since the DMA model is a good approximation to the DPM model, we can also adjust our model by applying a DMA prior for the specific cluster of the document. Then, the data set X can be generated. N is the number of clusters, the N-dimensional vector P is the mixing proportions for the clusters, and zd indicates the latent cluster allocation of the document xd. The graphical representation of the DMAFP model. Similar to (9), the probability density function of xd under the DMAFP model can be approximated as follows: |
| The introduction of the DMAFP model and the approximation (10) facilitates us to develop effective and fast variational inference algorithm as well as the Gibbs sampling algorithm similar to those for the finite mixture model. |
| In fact, since Dirichlet distribution is the conjugate prior for the parameter of multinomial distribution, integrating out η0 ,η1, , ηN in (10), the approximation of the conditional probability density function of the data set X given {z1, z2, . . . , zD} and γ can be represented as follows: |
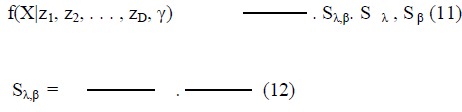 |
ONTOLOGIES |
| An ontology is a “a specification of a conceptualization” whereby a conceptualization is a collection of objects, concepts and other entities that are presumed to exist in some domain and that are tied together with some relationships. A conceptualization is a simplified view of the world, a way of thinking about some domain. Ontologies belong to the knowledge representation approaches that have been discussed above and they aim to provide a shared understanding of a domain both for the computers and for the humans. Thereby, ontology describes a domain of interest in such a formal way that computers can process it. The outcome is that the computer system knows about this domain. Ontology is a formal classification schema, which has a hierarchical order and which is related to some domain. An ontology comprises the logical component of a “Knowledge Base”. Typically, a knowledge base consists of an ontology, some data and also an inference mechanism. Ontology, comprising the logical component of the knowledge base, defines rules that formally describe how the field of interest looks like. The data can be any data related to this field of interest that is extracted from various resources such as databases, document collections, the Web etc. The inference mechanism would deploy rules in form of axioms, restrictions, logical consequences and other various methods based on the formal definition in the ontology over the actual data to produce more information out of the existing one. |
SEMANTIC ANALYSIS BASED DIRICHLET CLUSTERING SCHEME |
| Discriminative word identification process is improved with the labeled document analysis mechanism. Concept relationships are analyzed with Ontology support. Semantic weight model is used for the document similarity analysis. The system improves the scalability with the support of labels and concept relations for dimensionality reduction process. The DPMFP model is enhanced to perform the clustering with semantic analysis mechanism. Word categorization process is improved with label values. Label and concept details are used to identify the optimal cluster count value. The system is divided into five major modules. They are document preprocess, discrimination identification, concept analysis, feature analysis and clustering process. |
| 7.1. Document Preprocess |
| The document preprocess is performed to parse the documents into tokens. Stop word elimination process is applied to remove irrelevant terms. Stemming process is applied to carry term suffix analysis. Document vector is constructed with terms and their count values. |
| 7.2. Discrimination Identification |
| Term and its importance is estimated by the system. Statistical weight estimation process is applied with term and its count values. Term weight estimation is performed with Term Frequency (TF) and Inverse Document Frequency (IDF) values. Variational inference algorithm is used to perform partition of document words. |
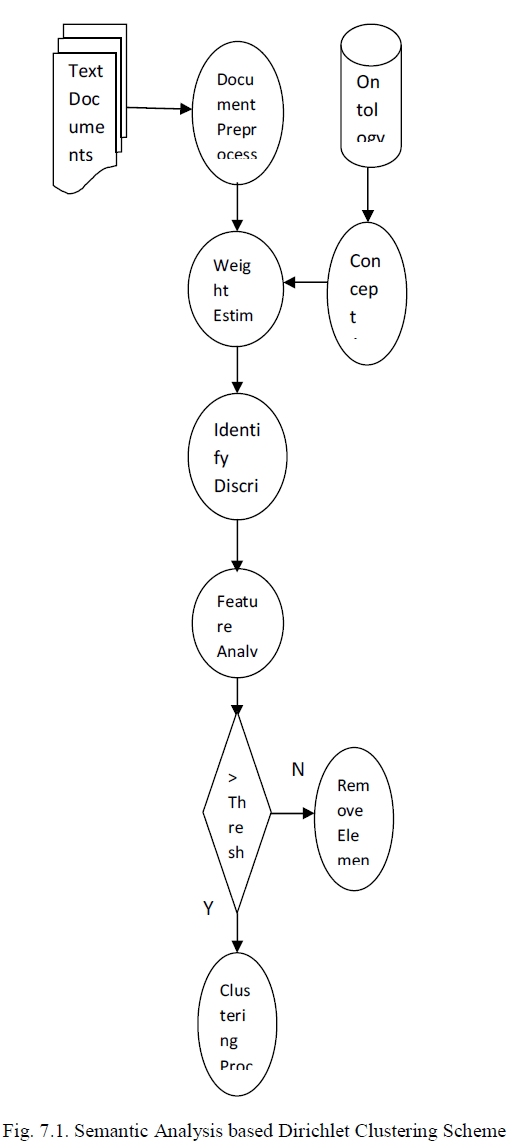 |
| 7.3. Concept Analysis |
| Concept analysis is performed to measure the term relationships. Ontology repository is used for the concept relationship identification. Concept weight is assigned for each document element. Element type and frequency values are used in the concept weight estimation process. |
| 7.4. Feature Analysis |
| Feature analysis is performed to identify the feature subspace in the documents. Term features and semantic features are extracted in the feature analysis. Statistical weight values are used in the term feature extraction process. Concept weights are used in the concept features extraction process. |
| 7.5. Clustering Process |
| Dirichlet Process Mixture Model for Feature Partition (DPMFP) mechanism is used to group up the documents. Cluster count estimation is carried out to find optimal partitions. Term features and concept features are used in the clustering process. Term and concept similarity analysis is used to measure the document relationships. |
CONCLUSION |
| Documents are grouped into an optimal number of clusters with automatic K estimate mechanism. Dirichlet Process Mixture Model for Feature Partition (DPMFP) scheme is used to partition the text documents. DPMFP scheme is enhanced to support clustering on labeled document environment. The clustering process is enhanced with concept relationship analysis mechanism. Clustering accuracy is improved in the system. Concept relationship based similarity analysis model id used for the document comparison process. The system reduces the process time and memory requirements for the document clustering process. Automatic cluster count estimate mechanism is used for optimal cluster count selection requirements. |
References |
|