ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Index Terms |
| Series of metric spaces, series of new convex and normalized functions, series of divergence measures, properties of convex functions and divergences. |
Mathematics Subject Classification |
| 94A17, 26D15. |
INTRODUCTION |
 |
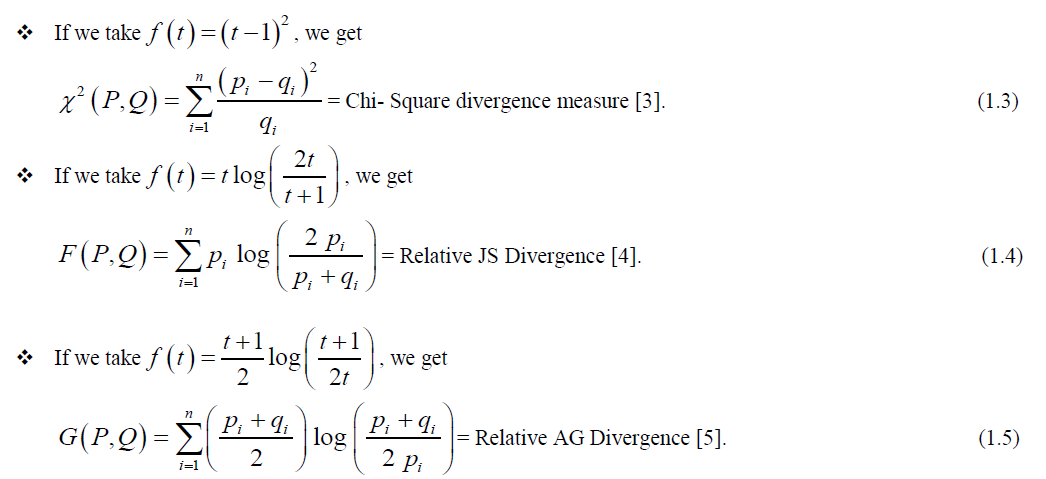 |
| Similarly, we get many others divergences as well by defining suitable convex function. |
| Many research papers have been studied of I.J. Taneja, P. Kumar, S.S. Dragomir, K.C. Jain and others, who gave the idea of divergence measures, their properties, their bounds and relations with other measures. These all are very useful because divergence measures are applied in variety of disciplines (mentioned in conclusion). We introduced a new form of these measures, i.e. metric spaces. We found that square root of all divergences of Csiszar’s class, is a metric space, which is very useful in functional analysis. We can extend this idea in functional analysis. |
SERIES OF CONVEX FUNCTIONS AND THEIR PROPERTIES |
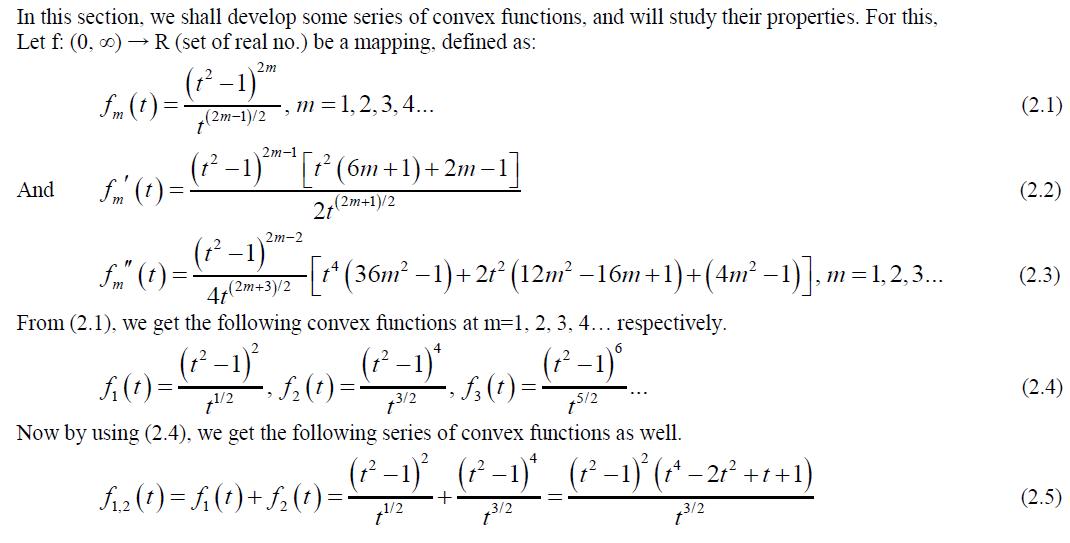 |
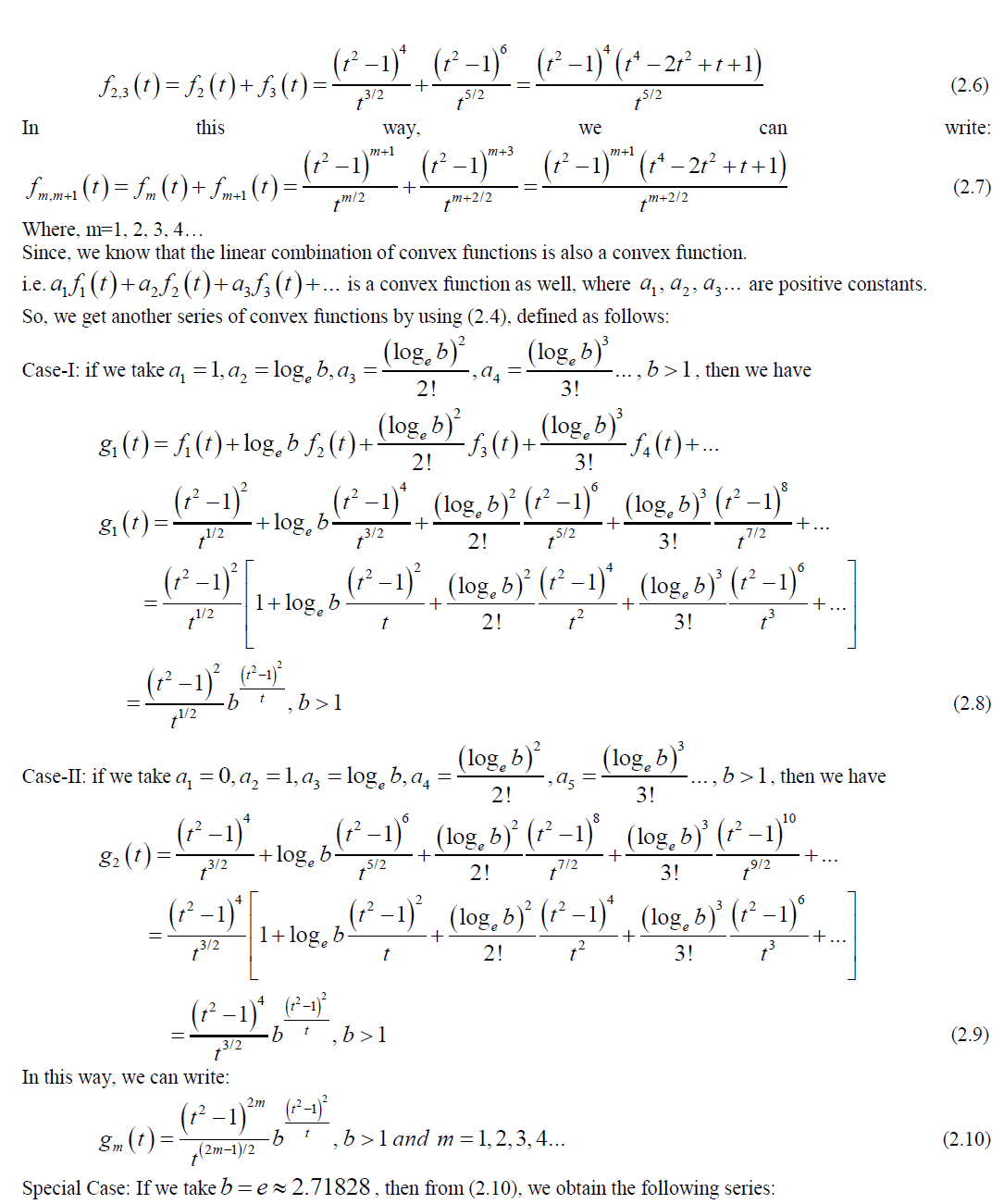 |
 |
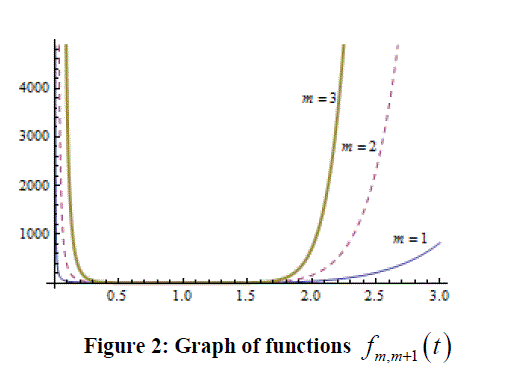 |
CORRESPONDING SERIES OF DIVERGENCES AND PROPERTIES |
| In this section, we shall obtain series of divergence measures corresponding to convex functions defined in section 2, and will study the properties. |
| The following theorem is well known in literature [1]. |
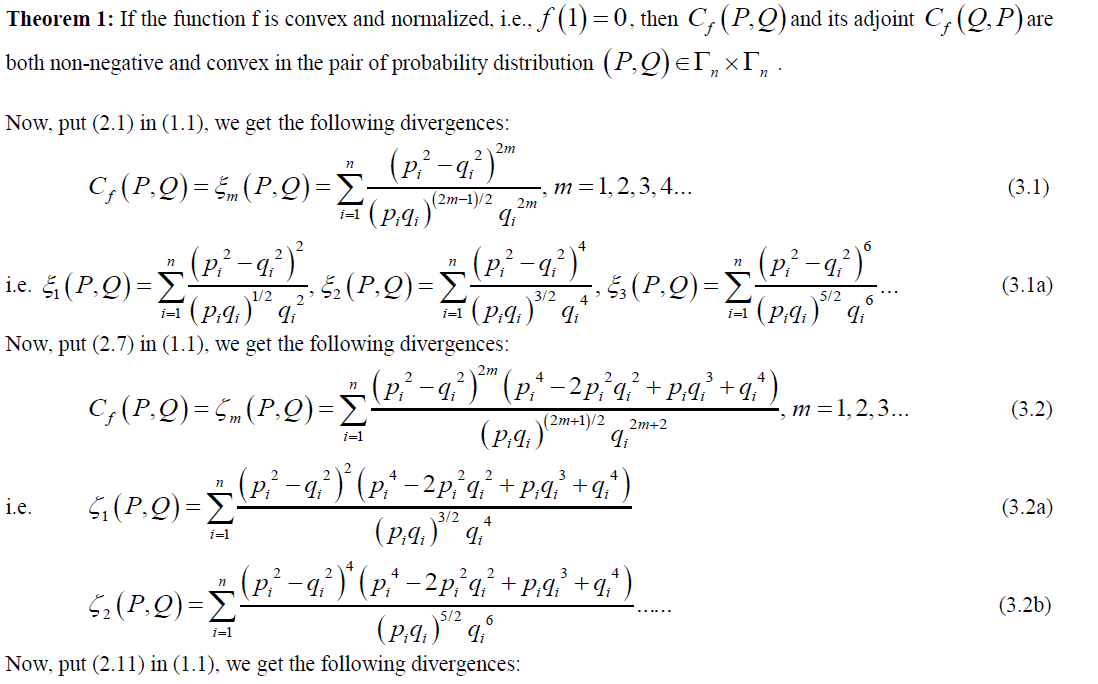 |
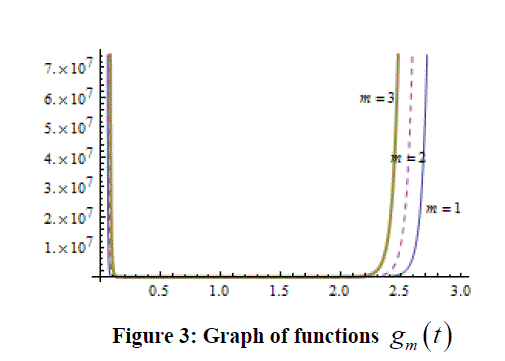 |
SERIES OF METRIC SPACES (DISTANCE MEASURES) |
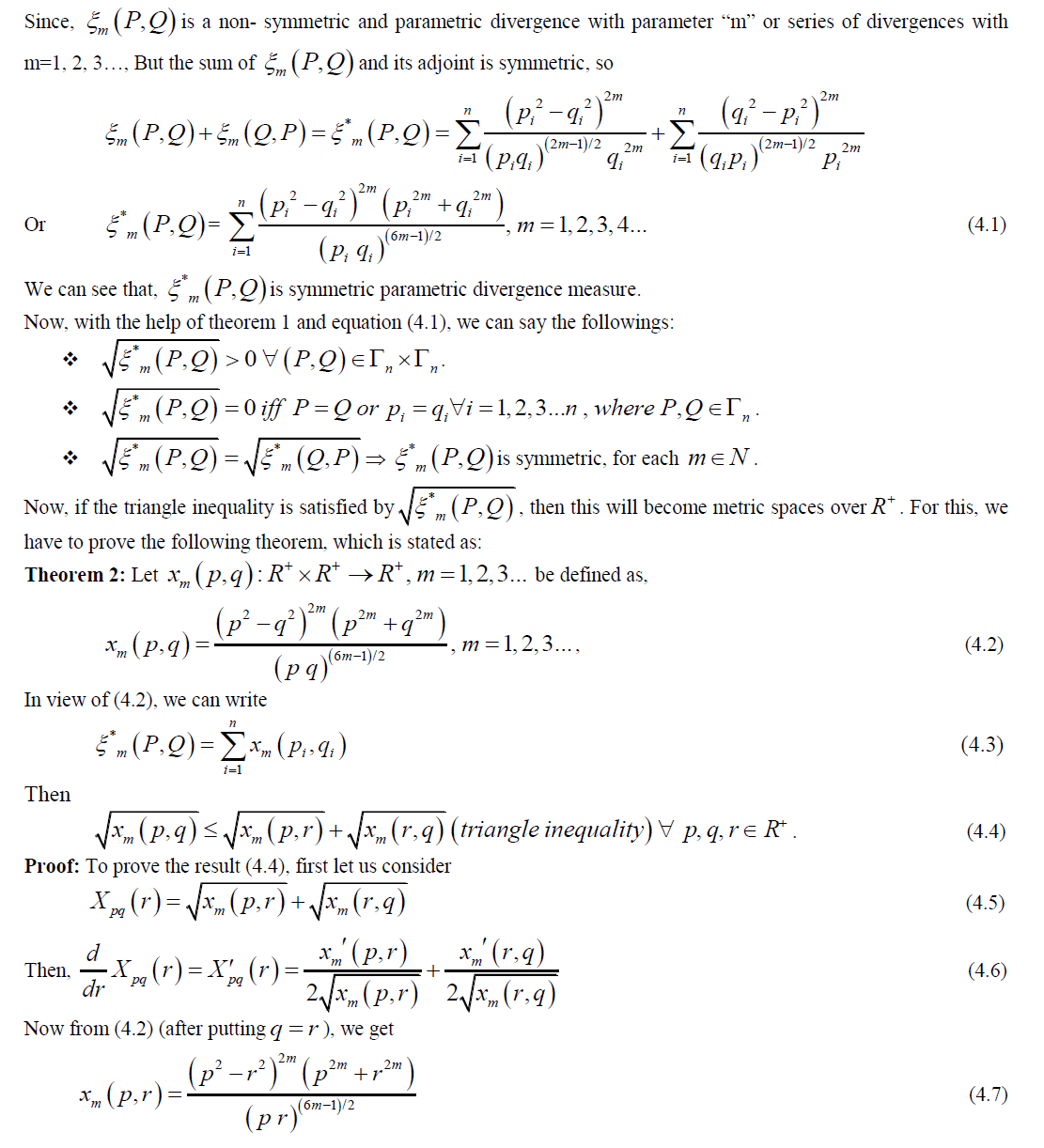 |
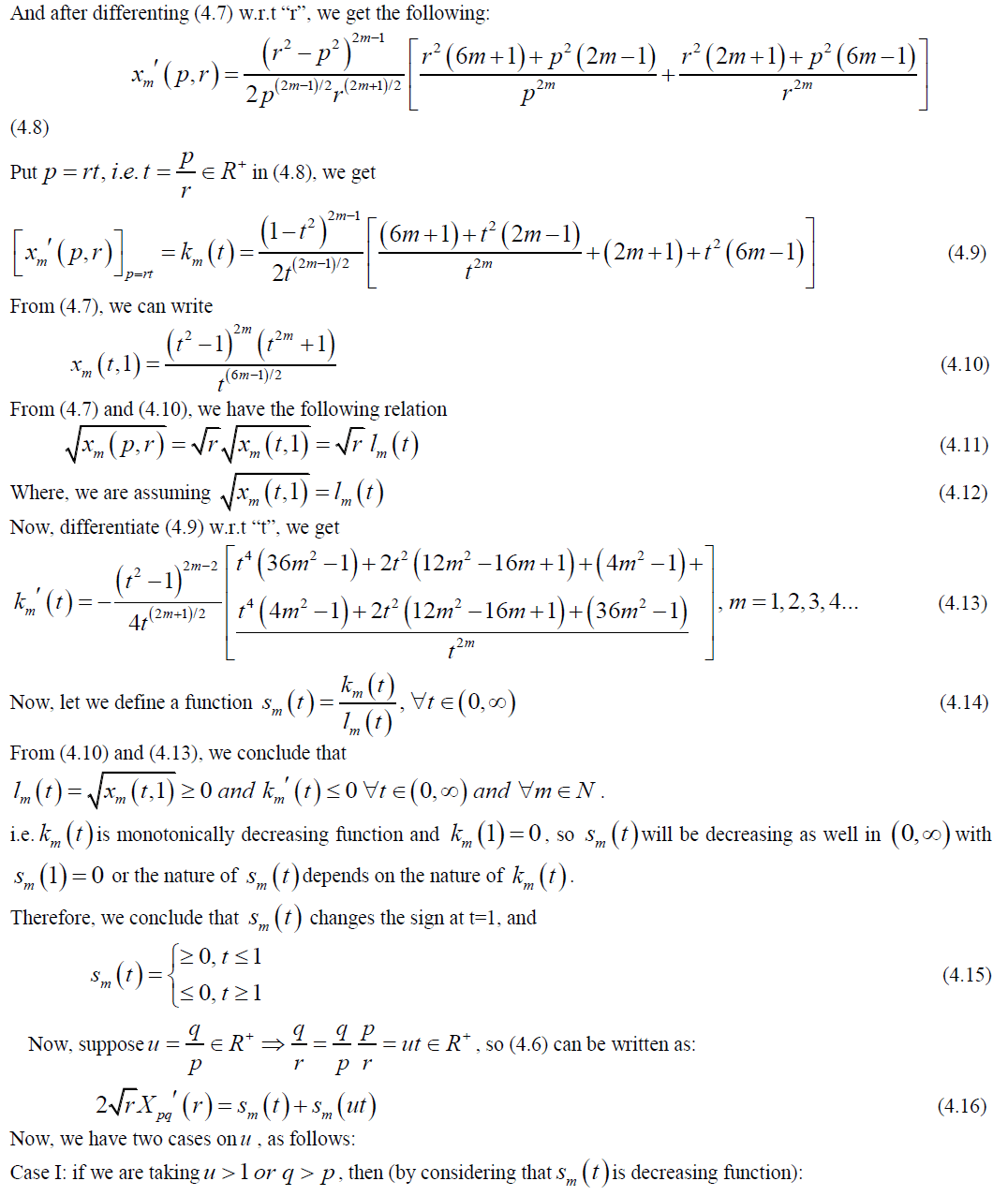 |
 |
CONCLUDING REMARKS |
| Divergence measures have been applied in a variety of disciplines such as anthropology, genetics, finance, economics and political science, biology, analysis of contingency tables, approximation of probability distributions, signal processing and pattern recognition. |
| In this paper, we introduced a new series of convex functions, new series of divergence measures and new series of metric spaces. |
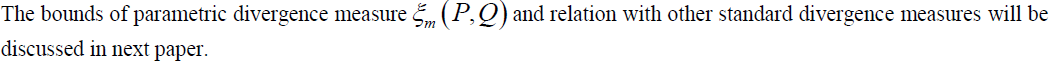 |
References |
| [1] Csiszar, I., “Information type measures of differences of probability distribution and indirect observations”, Studia Math. Hungarica, Vol. 2, pp. 299- 318, 1967. [2] Kullback S. and Leibler R.A., “On Information and Sufficiency”, Ann. Math. Statist., Vol. 22, pp. 79-86, 1951. [3] Pearson K., “On the Criterion that a given system of deviations from the probable in the case of correlated system of variables is such that it can be reasonable supposed to have arisen from random sampling”, Phil. Mag., Vol. 50, pp. 157-172, 1900. [4] Sibson R., “Information radius”, Z. Wahrs. Undverw. Geb., Vol. 14, pp. 149-160, 1969. [5] Taneja I.J., New developments in generalized information measures, Chapter in: Advances in Imaging and Electron Physics, Ed. P.W. Hawkes, Vol. 91, pp. 37-135, 1995. |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Divergence measures are basically measures of distance between two probability distributions or these are useful for comparing two probability distributions. Depending on the nature of the problem, the different divergences are suitable. So it is always desirable to create a new divergence measure. There are several generalized functional divergences, such as: Csiszar divergence, Renyi- like divergence, Bregman divergence, Burbea- Rao divergence etc. all. In this paper, we obtain a series of divergences corresponding to a series of convex functions by using generalized Csiszar divergence. Further, we define the properties of convex functions and divergences, compare the divergences and lastly introduce the series of metric spaces.
Index Terms |
| Series of metric spaces, series of new convex and normalized functions, series of divergence measures, properties of convex functions and divergences. |
Mathematics Subject Classification |
| 94A17, 26D15. |
INTRODUCTION |
 |
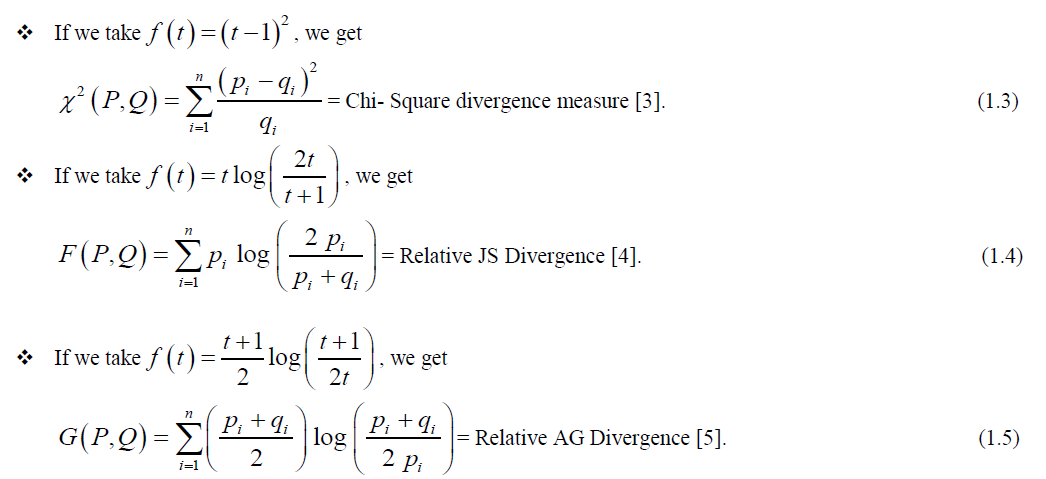 |
| Similarly, we get many others divergences as well by defining suitable convex function. |
| Many research papers have been studied of I.J. Taneja, P. Kumar, S.S. Dragomir, K.C. Jain and others, who gave the idea of divergence measures, their properties, their bounds and relations with other measures. These all are very useful because divergence measures are applied in variety of disciplines (mentioned in conclusion). We introduced a new form of these measures, i.e. metric spaces. We found that square root of all divergences of Csiszar’s class, is a metric space, which is very useful in functional analysis. We can extend this idea in functional analysis. |
SERIES OF CONVEX FUNCTIONS AND THEIR PROPERTIES |
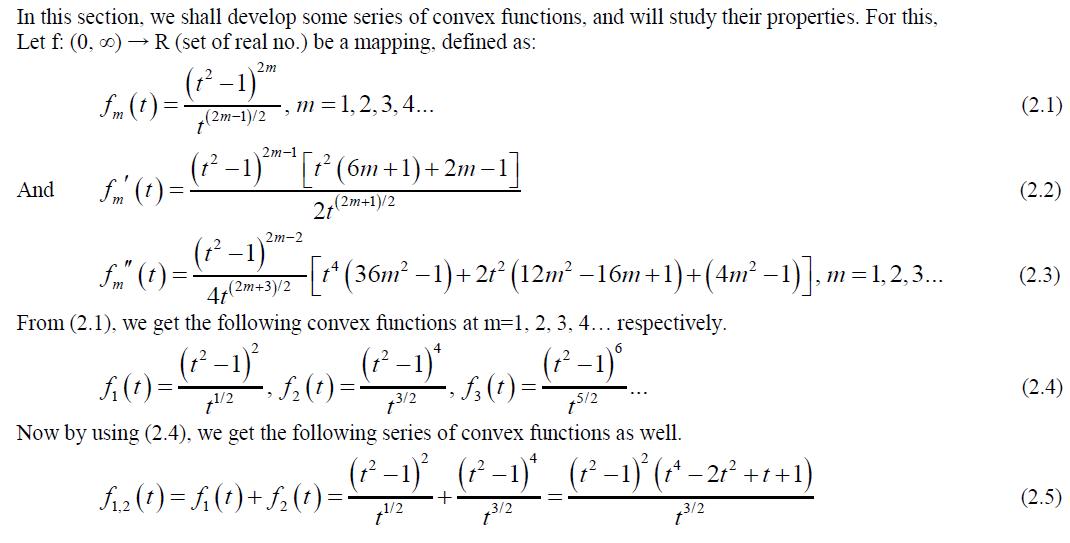 |
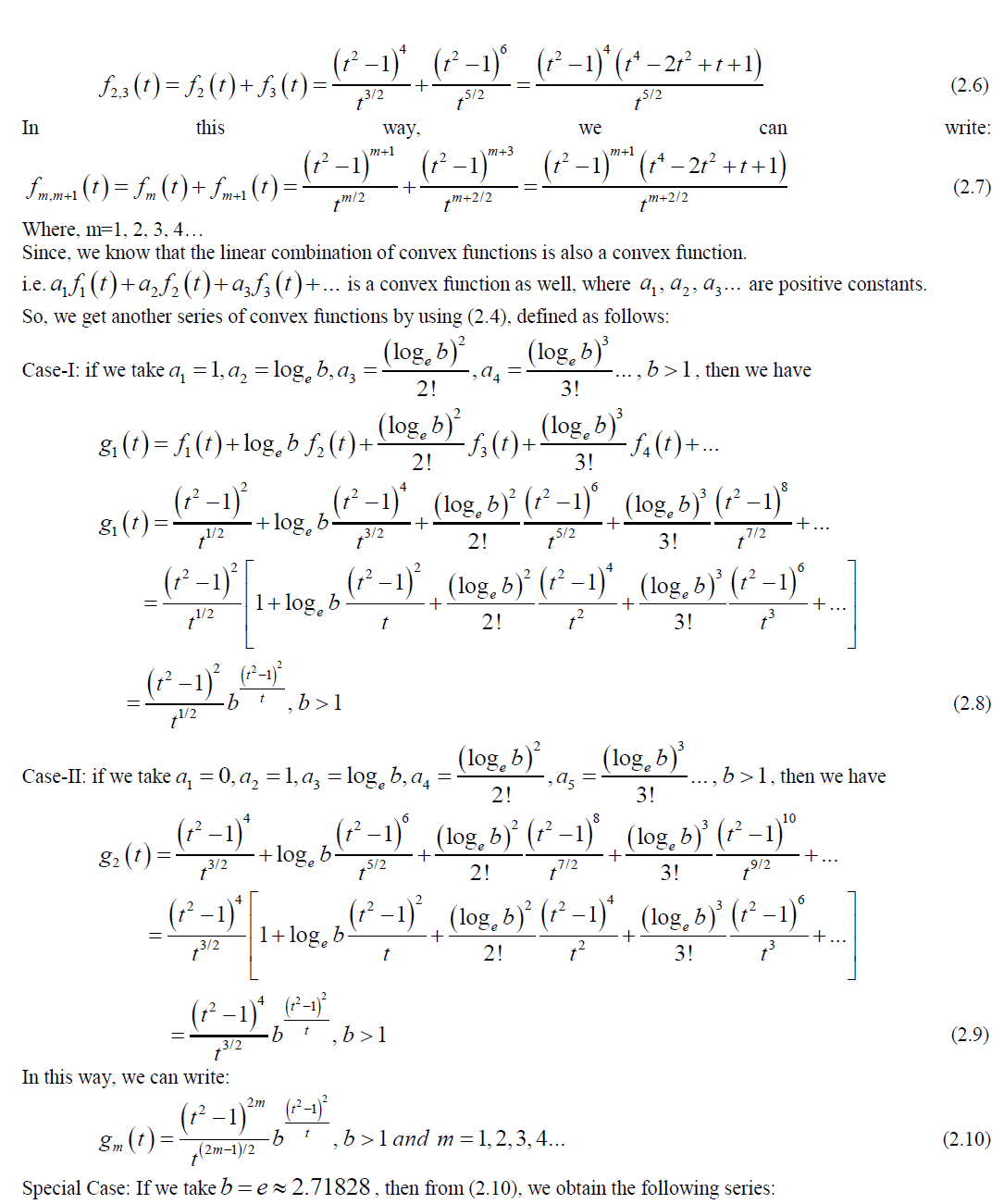 |
 |
 |
CORRESPONDING SERIES OF DIVERGENCES AND PROPERTIES |
| In this section, we shall obtain series of divergence measures corresponding to convex functions defined in section 2, and will study the properties. |
| The following theorem is well known in literature [1]. |
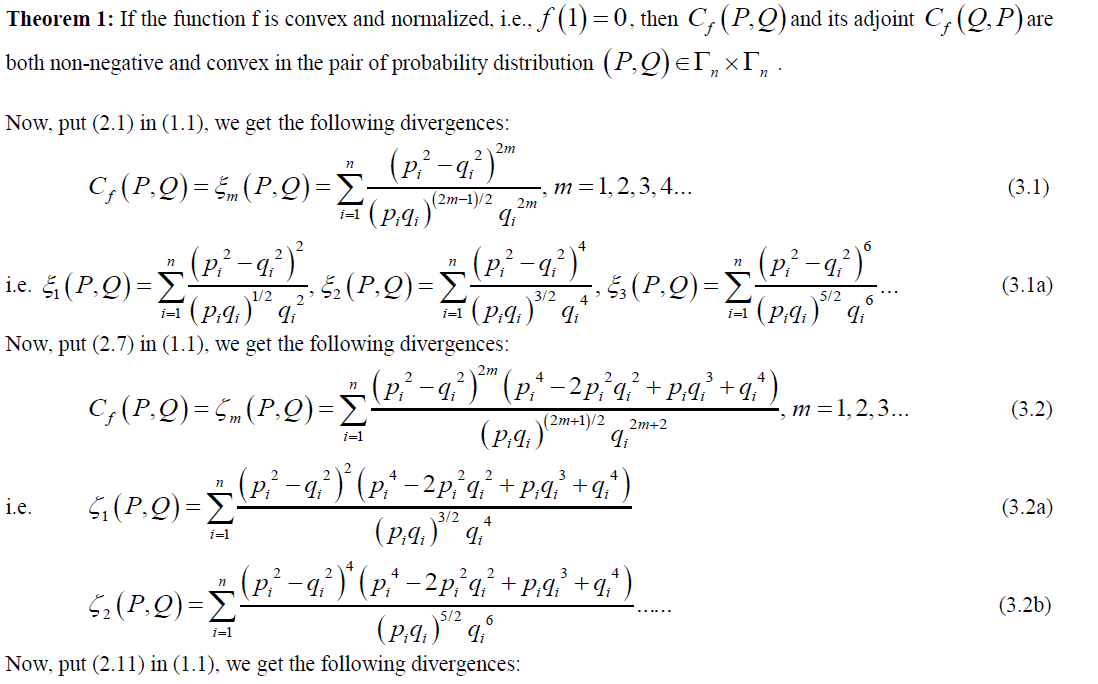 |
 |
SERIES OF METRIC SPACES (DISTANCE MEASURES) |
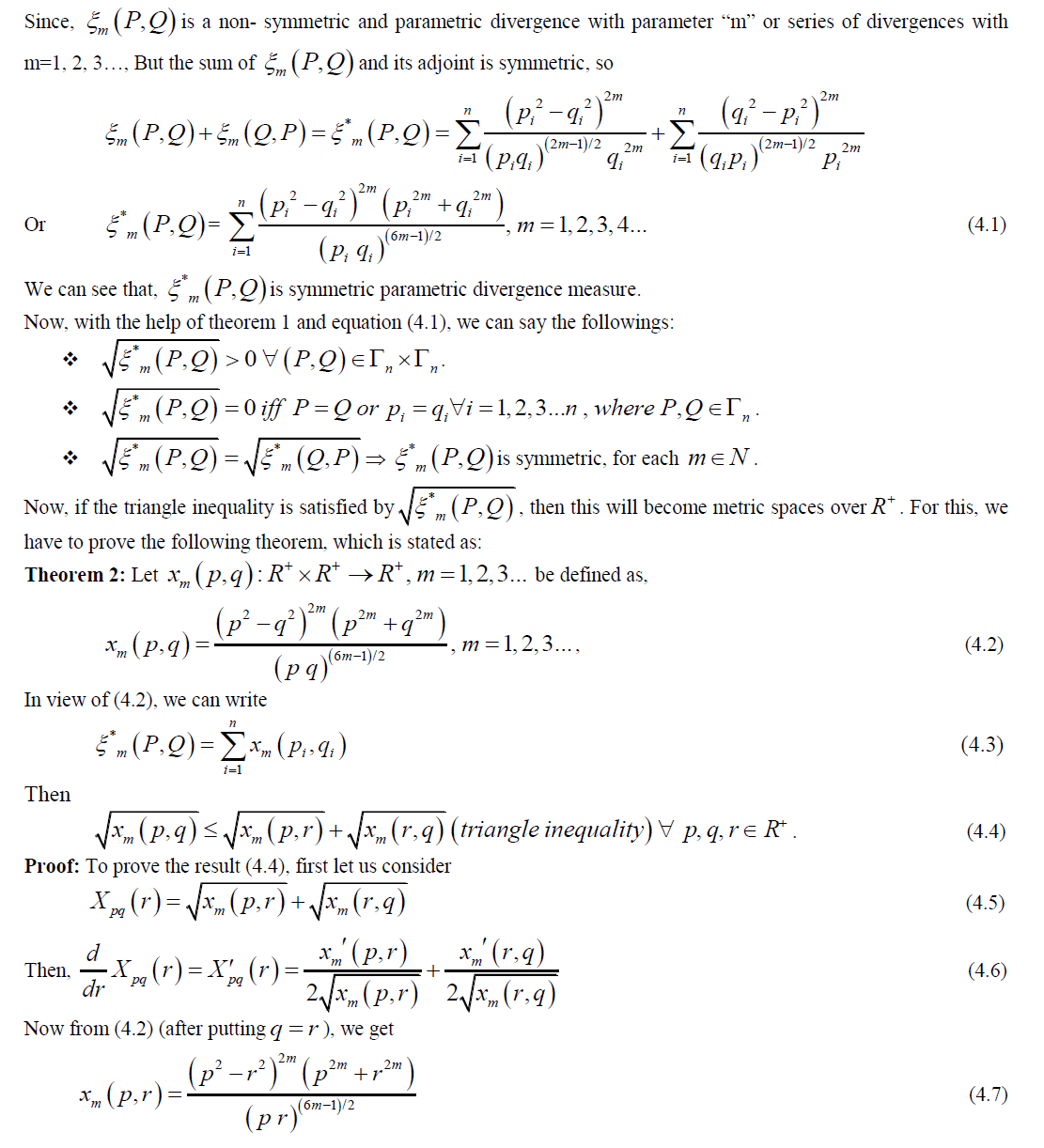 |
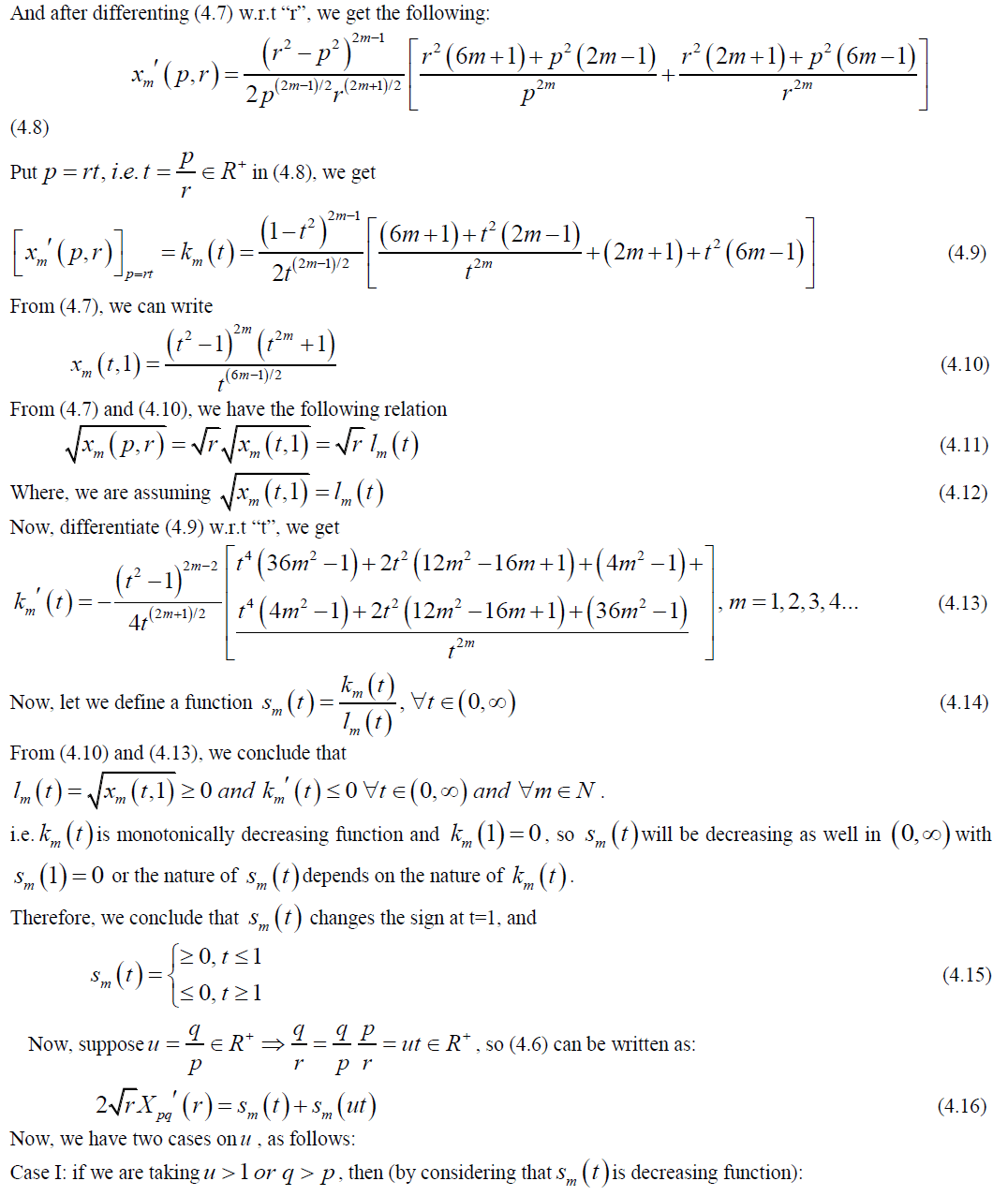 |
 |
CONCLUDING REMARKS |
| Divergence measures have been applied in a variety of disciplines such as anthropology, genetics, finance, economics and political science, biology, analysis of contingency tables, approximation of probability distributions, signal processing and pattern recognition. |
| In this paper, we introduced a new series of convex functions, new series of divergence measures and new series of metric spaces. |
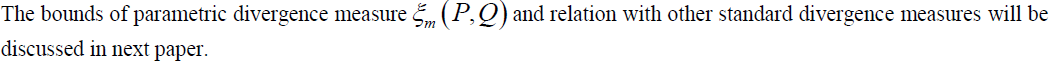 |
References |
|