Shift Strategy for Non-overdamped Quadratic Eigen-problems

Abstract

In this paper we study properties of non-overdamped quadratic eigen problems. For the non-overdamped Eigen-value problems we cannot apply variational characterization in full. One of the subintervals of the interval in which we can apply variational characterization for Eigen-values of a negative type is known. In this paper we expand this subinterval by giving better right boundry of the variational characterization interval. This is achieved by getting bigger lower boundary for δ+. New strategy is seen in fact that we join suitably selected hyperbolic quadratic pencil to non-overdamped quadratic pencil. From the variational characterization of the hyperbolic eigenproblem we get better lower boundary for δ+.

Keywords

Non-overdamped, Quadratic Eigen-problem, Hyperbolic Quadratic Eigen-problem, Varitional characterization, Quadratic pencil, Rayleigh functional, Shift strategy

Introduction

The quadratic Eigen-value problems have great application in practice. Tisseur and Meerbergen wrote in [1] about this application. The theoretical basics for the quadratic Eigen-value problems are given in the [2,3]. An important tool for finding Eigenvalues is variational characterization of the nonlinear Eigen-value problems [2,4,5]. The quadratic Eigen-value problems are a special case of the nonlinear Eigen-value problems and they are divided into overdamped and non-overdamped problems. Duffin [6] proved that for overdamped quadratic Eigen-value problems all Eigen-values λ₁ ≤ ⋯ ≤ λ_n and λ_n+1 ≤ λ _n+2 ≤ ⋯ ≤ λ_2n maxmin values of the functional p_- and p₊, respectively, and Rogers [7] generalized it to the finite dimensional overdamped case.

Kostić and Šikalo [8] have proposed improvement of existing methods which determine whether a quadratic pencil Q (λ is definite.

The non-overdamped quadratic problems tend to fall into the more difficult square Eigen problems because the variational characterization cannot be applied on them in full. The variational characterization for non-overdamped problems can be applied on 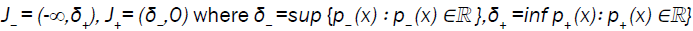The practical problem is that δ_- and δ₊ are usually not known.

Kostić and Voss in [9] considered non-overdamped problems and give upper bound of δ_- and lower bound of δ₊. They apply the Sylvester’s law of inertia, in suitable intervals, for a localization of the parameters. In this paper, we consider the improvement of the lower bound of δ₊ from the Kostić and Voss paper [9]. We join suitably selected hyperbolic quadratic pencil to the nonoverdamped quadratic pencil. The hyperbolic quadratic eigenproblem is suitable because it is overdamped and on it we can apply the variational characterization in full. From the hyperbolic quadratic problem, we also obtain a lower bound of δ₊.

In Section 2 of this paper we provide the basic terms about the variational characterization. In Section 3 we give basics of Sylvester’s law of inertia for nonlinear Eigen-value problems. In Section 4 we explain the hyperbolic Eigen-value pencil and its properties. Section 5 we consider non-overdamped problems and their properties. By applying information obtained from the consideration of the selected hyperbolic pencil we get in Section 6 a better lower bound for δ₊ and we apply Sylvester’s law of inertia on it. In Section 7 we give a conclusion and indications for further research.

Variational Characterization

Variational characterization is important for finding Eigen-values. In this paper we give a brief review of variational characterization of nonlinear Eigen-value problems. Since the quadratic eigen-problems are a special case of nonlinear Eigenvalue problems, results for nonlinear Eigen-value problems can be specially applied for the quadratic Eigen-value problems. Variational characterization is generalization of well-known minmax characterization for the linear Eigen-value problems.

We consider nonlinear Eigen-value problems

T (λ) x=0,   (1)

Where 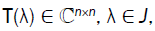is a family of the Hermitian matrices depending continuously on the parameter λ ∈ J and J is a real open interval which may be unbounded.

Problems of this type arise in damped vibrations of structures, conservative gyroscopic systems, lateral buckling problems, problems with retarded arguments, fluid-solid vibrations, and quantum dot hetero structures.

To generalize the variational characterization of Eigen-values we need a generalization of the Rayleigh quotient. To this end we assume that

A. for every fixed 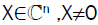the scalar real equation

f(λ; X):=X^HT(λ)X   (2)

has at most one solution p(x)∈ J. Then f(λ; x) =0, implicitly defines a functional on some subset D⊂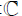 which is called the Rayleigh functional of (1).

A. for every x∈D and every λ∈J with λ ≠ p(x) it holds that (λ−p (x) ) f (λ; x) > 0.

If is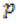 defined on D= 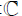\{0} then the problem (1) is called overdamped, otherwise it is called non-overdamped.

Generalizations of the minmax and the maxmin characterizations of the Eigen-values were proved by Duffin [6] for the quadratic case and by Rogers [7] for the general overdamped problems. For the non-overdamped Eigen-problems the natural ordering to call the smallest Eigen-value the first one, the second smallest the second one, etc., is not appropriate. The next theorem is poved in [2,4,5], which gives more information about the following minmax characterization for Eigen-values.

Theorem 1: Let J be an open interval in, and let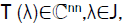 be a family of Hermitian matrices depending continuously on the parameter λ ∈ J, such that the conditions (A and (B are satisfied. Then the following statements hold.

• For every l ∈N there is at most one l^th Eigen-value of T (which can be characterized by

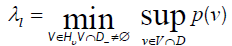(3)

• If

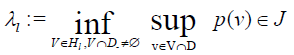
For some 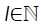then λ_ι is the1^th Eigen-value of T (.) in J, and (3) holds.

• If there exists the k^th and 1^th Eigen-value λ_κ and λ_ι in, J(k<l) then J contains the J^th Eigen-value λ_j (k ≤ j ≤ l) as well, and λ_k ≤ λ_j ≤ λ_l.

• Let λ_l= inf_x∈Dp(x)∈J and λ_l∈ J. If the minimum in (3) is attained for an l dimensional subspace V, then v⊃ D∪{0}, and (3) can be replaced with

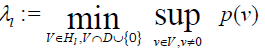
λ is an l^th Eigen-value if and only if μ=0 is the l^th Eigen-value of the linear eigenproblem T(λ)x=μx.

• The minimum in (3) is attained for the invariant subspace of T(λ_l) corresponding to its l_th largest Eigen-values.

Sylvester’s Law of Inertia

Sylvester´s law of inertia has an important role in the nonlinear Eigen-value problems. We will brefly look back to the Sylvester´s law of inertia. With this purpose we define the inertia of the Hermitian matrix т as follows.

Definition: The inertia of a Hermitian matrix т is the triplet of nonnegative integers In(T) =n_p, n_n, n_z

where n_p, n_n and n_z are the number of positive, negative, and zero Eigen-values of т (counting multiplicities.

Next we consider a case that an extreme Eigen-value is contained in J.

Theorem 2: Assume that T: J→^n×n satisfies the conditions of the minmax characterization, and let (n_p, n_n, n_z) be the inertia of T(σ) for some σ∈J.

If 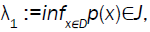then the nonlinear eigenproblem T(λ)X=0 has exactly np Eigen-values 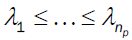in J which are less than σ.

If sup_x∈Dp(X)∈J, then the nonlinear eigenproblem T(λ)X=0 has exactly n_n Eigen-values 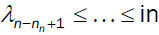J exceeding σ.

Hyperbolic Quadratic Pencil

For this study we will consider briefly a hyperbolic quadratic pencil. The hyperbolic quadratic pencil is overdamped. More accurately a quadratic matrix polynomial

Q(λ):= λ²A+λB+C, A=A^H>0, B=B^H, C=C^H (4)

is hyperbolic if for every x∈ⁿ, x≠0 the quadratic polynomial.

F(λ;x) := λ²x^HAx + λx^HBx + x^HCx =0 (5)

It has two distinct real roots:

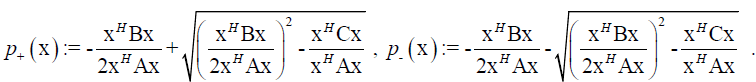(6)

The functionals in Equation (6) are the Rayleigh functionals of the quadratic matrix polynomial (Equation 5). The Rayleigh functionals are the generalization of the Rayleigh quotient.

The ranges 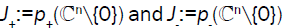are disjoint real intervals with maxJ_-<minJ₊. Q(λ) is the positive definite for λ<minJ_- and λ>minJ₊, and it is the negative definite for λε (maxJ_-, minJ₊ ).

(Q,J₊ ) and (-Q,J_-) satisfy the conditions of the variational characterization of the Eigen-values, i.e. there exist 2n Eigen-values [1].

λ₁ ≤ λ₂ ≤ … ≤ _n < _n+1 ≤ … ≤ λ_2n (7)

and

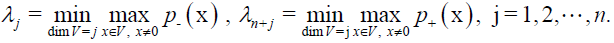(8)

Non-overdamped Quadratic Pencil

Here we will consider a special case of non-overdamped Eigen-value problems. We review the quadratic matrix pencils

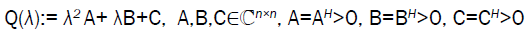(9)

Then for x ≠ 0 the two complex roots of f(λ;x):= x^HQ(λ)x are given as in Section 4 with

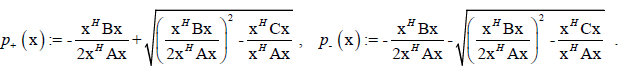(11)

Between these complex roots (10) and (11) there are all Eigen-values of the corresponding Eigen-value problem Q(λ)x=0.

Eigen-values obtained by the functional (10 are called Eigen-values of positive type. Eigen-values obtained by the functional (11) are called Eigen-values of negative type. For the eigenvector x ≠ 0 there is Q(λ)x=0 and therefore f(λ;x):= x^HQ(λ)x=0. For positive definite matrix A, B, C if p₊ (x) and p_- (x) are real then they are negative and therefore all real Eigen-values are negative. Let

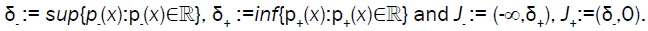
If f(; x)>0 for x ≠ 0 and λ∈ the Eigen-values problem Q(λ) x=0 has no real Eigen-values, but this has not to be known in advance.

Then all Eigen-values in J_- are min max values of p_-

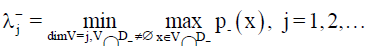
and all Eigen-values in J₊ are maxmin values of p₊.

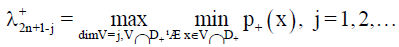
Our problem is existence of the possibility that δ₊ < δ_-. Such situation is given in Figure 1.

Following Figure 2 is representation of the quadratic polynomial f(λ; a) and f(λ; b) where a is eigenvector which belongs to the Eigen-value of the positive type λ=-5 and b is eigenvector that belongs to Eigen-value of negative type λ= -4.3.

For σ<δ₊ and for σ<δ_- we obtain slicing results for spectrum of the Q(.) from Theorem 2. If In(Q(σ)) = (n_p, n_n, n_z) and, then there exist n_n Eigen-values of the Q(.) in (-∞, σ) and if σ ∈ (δ-, 0) then there are n_n Eigen-values in (σ, 0). However, δ₊ and δ_- are usually not known. Kostić and Voss in [4] have proved following theorems. These theorems are significant because they give upper bounds of δ_- and lower bounds of δ₊ thus yielding subintervals of (-∞,δ₊) and (δ_-,0) where the above slicing applies.

Theorem 3: Let A, B, C ∈ ^n×n be positive definite, and let p₊ and p_- be defined in (10) and (11). Then is holds that

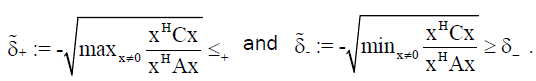(12)

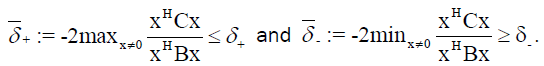(13)

Theorem 4: Let A, B, C ∈ 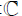^n×n be positive definite, and for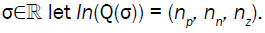

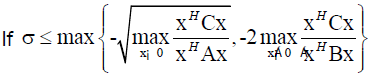
then there exists n_n Eigen-values of Q(λ)x=0 in (-∞, σ).

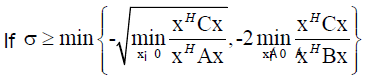
then there exists n_n Eigen-values of Q(λ)x=0 in (σ, 0).

Shift Strategy

Here we consider a non-overdamped pencil (9). To this overdamped pencil we will join a corresponding hyperbolic quadratic pencil. The hyperbolic quadratic pencil is suitable for us because it is overdamped which means for every x∈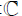ⁿ, x≠0 a corresponding hyperbolic quadratic pencil has two distinct real roots. Duffin in [6] has proved that the hyperbolic quadratic eigenproblem satisfies conditions of the variational characterization of the Eigen-values.

Let 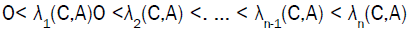Eigen-values of the Eigen-value problems 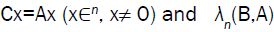is maximal Eigen-value of the Eigen-value problems Bx=Ax (x∈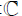ⁿ, x≠ 0).

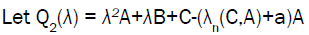(14)

Be a quadratic pencil where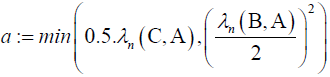

Theorem 5: Quadratic pencil (14) is hyperbolic.

Proof: It is clearly seen from the definition of quadratic pencil that matrices A, B and C-(λ_n(C,A)+a) A are Hermitian matrices.

By using 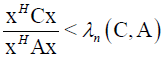and a>0 we get 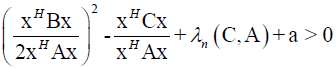which means that our pencil is hyperbolic.

Appropriate functional for our hyperbolic pencil (14) are:

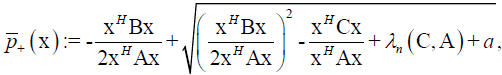(15)

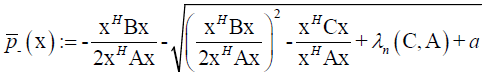(16)

The ranges 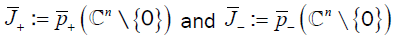are disjoint real intervals with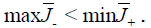

Theorem 6: Let 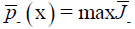then for every 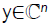for which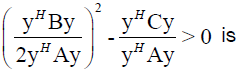

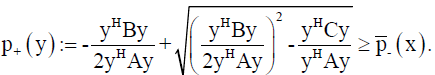(17)

Proof: Suppose the contrary that exists y∈Cⁿ for which 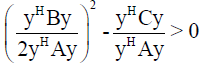for which

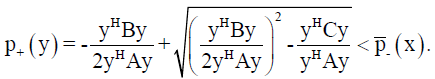(18)

i.e.

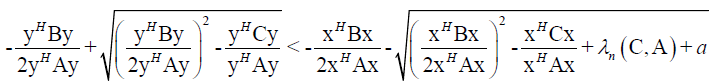
From this follows

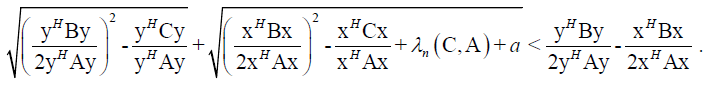(19)

If

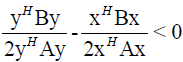
We get a contradiction. Because of this we take that

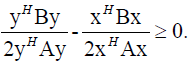
After squaring (19) and editing we get

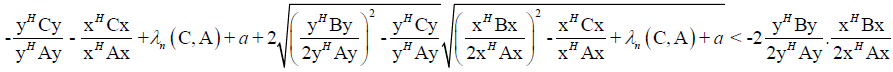(20)

Now we have two cases

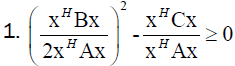
From (20 follows

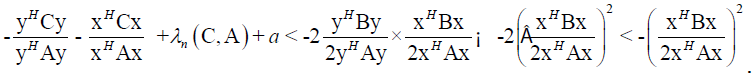
It follows

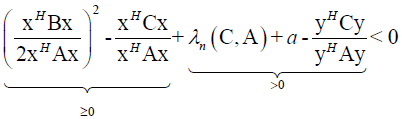,which is contradiction, so Theorem 6 stands.

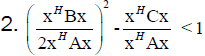
From (20) follows

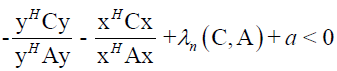(21)

We have here two cases

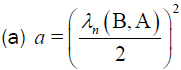
From (21) follows

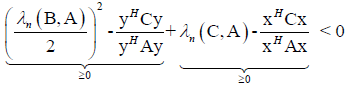,Which is contradiction, so Theorem 6 stands.

(b) a = 0.5.λ_n (C, A) We have here two cases

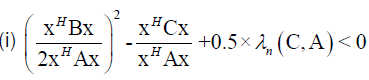
From

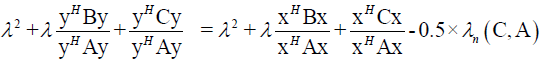and (18) follows

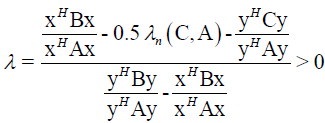(22)

From (22) and 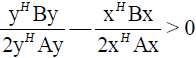follows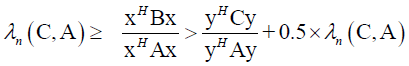

So, it follows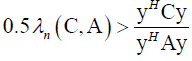

By using from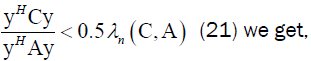

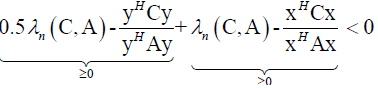
which is contradiction, so Theorem 6 stands.(ii)

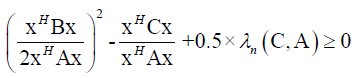
From (20) follows

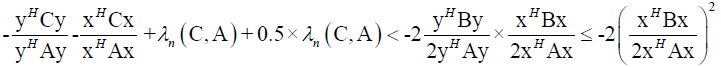
It follows

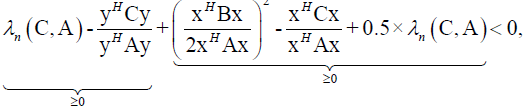
Which is contradiction, so Theorem 6 stands.

In this way we get the following improvement of the Theorem 7 and the Theorem 8.

Theorem 7: Let A, B, C ∈ 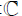^n×n be positive definite, and let p₊ and p_- be defined in (10 and (11. Then is holds that

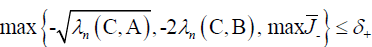
and

Next example illustrates that with the Theorem 7 we get a better lower boundary ₊ than with Theorem 3.

Example: Quadratic pencil

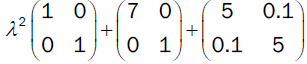is non-overdamped. This quadratic pencil has two complex Eigen-values -0.5002+2.1794i and -0.5002-2.1794i.

This pencil has Eigen-value of negative type -6.1926 and Eigen-value of a positive type -0.807.

Corresponding hyperbolic pencil is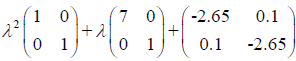

applying Theorem 3 we get lower boundary -2.2583 for δ₊. By applying Theorem 7 we get lower boundary -2.2027 for δ₊. Since we obtained bigger lower boundary we got an improvement.

Theorem 8: Let A, B, C ∈ 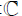^n×n be positive definite, and for σ∈ et In (Q (σ)) = (n_p, n_n, n_z).

If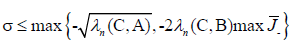

Where 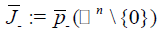then there exists n_n Eigen-values of Q (λ) x=0 in (-∞,σ).

If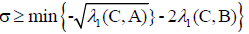

Then there exists n_n Eigen-values of Q (λ) x=0 in(σ,0).

Conclusion

In this paper, we considered a special class of the quadratic Eigen-value problems, non-overdamped problems. The nonoverdamped problems are often seen in practice. Although the non-overdamped problems are seen in practice, because of the mathematical difficulty of this problem they are not often a subject of the research. This was motivation for their wider consideration. The overdamped problems are difficult for the consideration because the variational characterization can only partly be applied on them. Because of this in literature exists upper bound of δ+. I this paper we considered the improvement of the lower bound of δ₊. We introduced completely new strategy for the determination of better lower bound of δ+. This strategy is based in the obtaining additional information from the conveniently chosen hyperbolic Eigen-value problem. In the further research we will try to improve upper bound of δ_-.

References

1. Tisseur F, et al.  The quadratic Eigen-value problem. SIAM Review 2001; 43:235-286.
2. Katsikis VN.  Applied linear algebra in action. 2016.
3. Veselić K. Damped oscillations of linear systems - A mathematical introduction, Springer Lecture Notes in Mathematics. 2023.
4. Voss H. A minmax principle for nonlinear Eigen-problems depending continuously on the Eigen-parameter. Numer Lin Algebra Appl. 2009; 16:899-913.
5. Voss  H, et al. A minimax principle for nonlinear Eigen-value problems with applications to nonoverdamped systems. Math Meth Appl Sci. 1982; 4:415-424.
6. Duffin RJ. A minimax theory for overdamped networks. J Rat Mech Anal. 1955; 4:221-233.
7. Rogers E. A minimax theory for overdamped systems. Arch Ration Mech Anal. 1964; 16:89-96.
8. Kosti A, et al. Definite quadratic Eigen-value problems. Procedia Engineering 2015; 100:56-63.
9. Kostić A, et al. On Sylvester's law of inertia for nonlinear Eigen-value problems. Electr Trans Numer Anal. 2013; 40:82-93.