Uiverzitet u Sarajevu, Mašinski fakultet, Bosnia and Herzegovina
Received date: 27/09/2016 Accepted date: 22/11/2016 Published date: 10/11/2016
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
In this paper we study properties of non-overdamped quadratic eigen problems. For the non-overdamped Eigen-value problems we cannot apply variational characterization in full. One of the subintervals of the interval in which we can apply variational characterization for Eigen-values of a negative type is known. In this paper we expand this subinterval by giving better right boundry of the variational characterization interval. This is achieved by getting bigger lower boundary for δ+. New strategy is seen in fact that we join suitably selected hyperbolic quadratic pencil to non-overdamped quadratic pencil. From the variational characterization of the hyperbolic eigenproblem we get better lower boundary for δ+.
Non-overdamped, Quadratic Eigen-problem, Hyperbolic Quadratic Eigen-problem, Varitional characterization, Quadratic pencil, Rayleigh functional, Shift strategy
The quadratic Eigen-value problems have great application in practice. Tisseur and Meerbergen wrote in [1] about this application. The theoretical basics for the quadratic Eigen-value problems are given in the [2,3]. An important tool for finding Eigenvalues is variational characterization of the nonlinear Eigen-value problems [2,4,5]. The quadratic Eigen-value problems are a special case of the nonlinear Eigen-value problems and they are divided into overdamped and non-overdamped problems. Duffin [6] proved that for overdamped quadratic Eigen-value problems all Eigen-values λ1 ≤ ⋯ ≤ λn and λn+1 ≤ λ n+2 ≤ ⋯ ≤ λ2n maxmin values of the functional p- and p+, respectively, and Rogers [7] generalized it to the finite dimensional overdamped case.
Kostić and Šikalo [8] have proposed improvement of existing methods which determine whether a quadratic pencil Q (λ is definite.
The non-overdamped quadratic problems tend to fall into the more difficult square Eigen problems because the variational
characterization cannot be applied on them in full. The variational characterization for non-overdamped problems can be applied
on 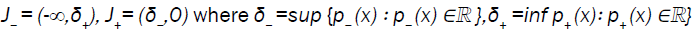 The practical problem is that δ- and δ+ are usually
not known.
The practical problem is that δ- and δ+ are usually
not known.
Kostić and Voss in [9] considered non-overdamped problems and give upper bound of δ- and lower bound of δ+. They apply the Sylvester’s law of inertia, in suitable intervals, for a localization of the parameters. In this paper, we consider the improvement of the lower bound of δ+ from the Kostić and Voss paper [9]. We join suitably selected hyperbolic quadratic pencil to the nonoverdamped quadratic pencil. The hyperbolic quadratic eigenproblem is suitable because it is overdamped and on it we can apply the variational characterization in full. From the hyperbolic quadratic problem, we also obtain a lower bound of δ+.
In Section 2 of this paper we provide the basic terms about the variational characterization. In Section 3 we give basics of Sylvester’s law of inertia for nonlinear Eigen-value problems. In Section 4 we explain the hyperbolic Eigen-value pencil and its properties. Section 5 we consider non-overdamped problems and their properties. By applying information obtained from the consideration of the selected hyperbolic pencil we get in Section 6 a better lower bound for δ+ and we apply Sylvester’s law of inertia on it. In Section 7 we give a conclusion and indications for further research.
Variational Characterization
Variational characterization is important for finding Eigen-values. In this paper we give a brief review of variational characterization of nonlinear Eigen-value problems. Since the quadratic eigen-problems are a special case of nonlinear Eigenvalue problems, results for nonlinear Eigen-value problems can be specially applied for the quadratic Eigen-value problems. Variational characterization is generalization of well-known minmax characterization for the linear Eigen-value problems.
We consider nonlinear Eigen-value problems
T (λ) x=0, (1)
Where 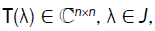 is a family of the Hermitian matrices depending continuously on the parameter λ ∈ J and J is a real
open interval which may be unbounded.
is a family of the Hermitian matrices depending continuously on the parameter λ ∈ J and J is a real
open interval which may be unbounded.
Problems of this type arise in damped vibrations of structures, conservative gyroscopic systems, lateral buckling problems, problems with retarded arguments, fluid-solid vibrations, and quantum dot hetero structures.
To generalize the variational characterization of Eigen-values we need a generalization of the Rayleigh quotient. To this end we assume that
A. for every fixed 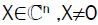 the scalar real equation
the scalar real equation
f(λ; X):=XHT(λ)X (2)
has at most one solution p(x)∈ J. Then f(λ; x) =0, implicitly defines a functional on some subset D⊂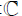 which is called the
Rayleigh functional of (1).
which is called the
Rayleigh functional of (1).
A. for every x∈D and every λ∈J with λ ≠ p(x) it holds that (λ−p (x) ) f (λ; x) > 0.
If is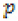 defined on D=
defined on D= 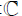 \{0} then the problem (1) is called overdamped, otherwise it is called non-overdamped.
\{0} then the problem (1) is called overdamped, otherwise it is called non-overdamped.
Generalizations of the minmax and the maxmin characterizations of the Eigen-values were proved by Duffin [6] for the quadratic case and by Rogers [7] for the general overdamped problems. For the non-overdamped Eigen-problems the natural ordering to call the smallest Eigen-value the first one, the second smallest the second one, etc., is not appropriate. The next theorem is poved in [2,4,5], which gives more information about the following minmax characterization for Eigen-values.
Theorem 1: Let J be an open interval in, and let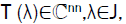 be a family of Hermitian matrices depending continuously
on the parameter λ ∈ J, such that the conditions (A and (B are satisfied. Then the following statements hold.
be a family of Hermitian matrices depending continuously
on the parameter λ ∈ J, such that the conditions (A and (B are satisfied. Then the following statements hold.
• For every l ∈N there is at most one lth Eigen-value of T (which can be characterized by
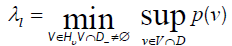 (3)
(3)
• If
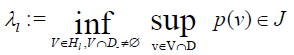
For some 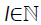 then λι is the1th Eigen-value of T (.) in J, and (3) holds.
then λι is the1th Eigen-value of T (.) in J, and (3) holds.
• If there exists the kth and 1th Eigen-value λκ and λι in, J(k<l) then J contains the Jth Eigen-value λj (k ≤ j ≤ l) as well, and λk ≤ λj ≤ λl.
• Let λl= infx∈Dp(x)∈J and λl∈ J. If the minimum in (3) is attained for an l dimensional subspace V, then v⊃ D∪{0}, and (3) can be replaced with
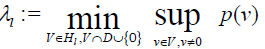
λ is an lth Eigen-value if and only if μ=0 is the lth Eigen-value of the linear eigenproblem T(λ)x=μx.
• The minimum in (3) is attained for the invariant subspace of T(λl) corresponding to its lth largest Eigen-values.
Sylvester’s Law of Inertia
Sylvester´s law of inertia has an important role in the nonlinear Eigen-value problems. We will brefly look back to the Sylvester´s law of inertia. With this purpose we define the inertia of the Hermitian matrix т as follows.
Definition: The inertia of a Hermitian matrix т is the triplet of nonnegative integers In(T) =np, nn, nz
where np, nn and nz are the number of positive, negative, and zero Eigen-values of т (counting multiplicities.
Next we consider a case that an extreme Eigen-value  is contained in J.
is contained in J.
Theorem 2: Assume that T: J→ n×n satisfies the conditions of the minmax characterization, and let (np, nn, nz) be the inertia
of T(σ) for some σ∈J.
n×n satisfies the conditions of the minmax characterization, and let (np, nn, nz) be the inertia
of T(σ) for some σ∈J.
If 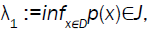 then the nonlinear eigenproblem T(λ)X=0 has exactly np Eigen-values
then the nonlinear eigenproblem T(λ)X=0 has exactly np Eigen-values 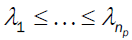 in J which are less
than σ.
in J which are less
than σ.
If supx∈Dp(X)∈J, then the nonlinear eigenproblem T(λ)X=0 has exactly nn Eigen-values 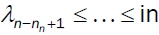 J exceeding σ.
J exceeding σ.
Hyperbolic Quadratic Pencil
For this study we will consider briefly a hyperbolic quadratic pencil. The hyperbolic quadratic pencil is overdamped. More accurately a quadratic matrix polynomial
Q(λ):= λ2A+λB+C, A=AH>0, B=BH, C=CH (4)
is hyperbolic if for every x∈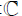 n, x≠0 the quadratic polynomial.
n, x≠0 the quadratic polynomial.
F(λ;x) := λ2xHAx + λxHBx + xHCx =0 (5)
It has two distinct real roots:
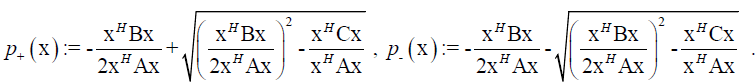 (6)
(6)
The functionals in Equation (6) are the Rayleigh functionals of the quadratic matrix polynomial (Equation 5). The Rayleigh functionals are the generalization of the Rayleigh quotient.
The ranges 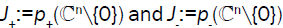 are disjoint real intervals with maxJ-<minJ+. Q(λ) is the positive definite for λ<minJ-
and λ>minJ+, and it is the negative definite for λε (maxJ-, minJ+ ).
are disjoint real intervals with maxJ-<minJ+. Q(λ) is the positive definite for λ<minJ-
and λ>minJ+, and it is the negative definite for λε (maxJ-, minJ+ ).
(Q,J+ ) and (-Q,J-) satisfy the conditions of the variational characterization of the Eigen-values, i.e. there exist 2n Eigen-values [1].
λ1 ≤ λ2 ≤ … ≤ n < n+1 ≤ … ≤ λ2n (7)
and
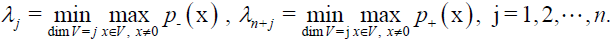 (8)
(8)
Non-overdamped Quadratic Pencil
Here we will consider a special case of non-overdamped Eigen-value problems. We review the quadratic matrix pencils
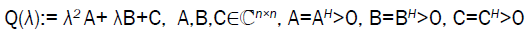 (9)
(9)
Then for x ≠ 0 the two complex roots of f(λ;x):= xHQ(λ)x are given as in Section 4 with
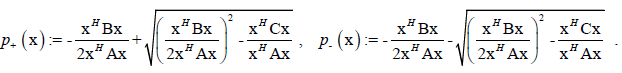 (11)
(11)
Between these complex roots (10) and (11) there are all Eigen-values of the corresponding Eigen-value problem Q(λ)x=0.
Eigen-values obtained by the functional (10 are called Eigen-values of positive type. Eigen-values obtained by the functional (11) are called Eigen-values of negative type. For the eigenvector x ≠ 0 there is Q(λ)x=0 and therefore f(λ;x):= xHQ(λ)x=0. For positive definite matrix A, B, C if p+ (x) and p- (x) are real then they are negative and therefore all real Eigen-values are negative. Let
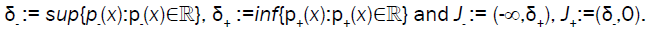
If f(; x)>0 for x ≠ 0 and λ∈ 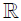 the Eigen-values problem Q(λ) x=0 has no real Eigen-values, but this has not to be known in
advance.
the Eigen-values problem Q(λ) x=0 has no real Eigen-values, but this has not to be known in
advance.
Then all Eigen-values in J- are min max values of p-
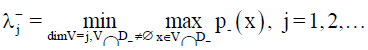
and all Eigen-values in J+ are maxmin values of p+.
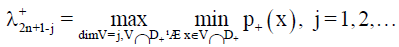
Our problem is existence of the possibility that δ+ < δ-. Such situation is given in Figure 1.
Following Figure 2 is representation of the quadratic polynomial f(λ; a) and f(λ; b) where a is eigenvector which belongs to the Eigen-value of the positive type λ=-5 and b is eigenvector that belongs to Eigen-value of negative type λ= -4.3.
For σ<δ+ and for σ<δ- we obtain slicing results for spectrum of the Q(.) from Theorem 2. If In(Q(σ)) = (np, nn, nz) and, then there exist nn Eigen-values of the Q(.) in (-∞, σ) and if σ ∈ (δ-, 0) then there are nn Eigen-values in (σ, 0). However, δ+ and δ- are usually not known. Kostić and Voss in [4] have proved following theorems. These theorems are significant because they give upper bounds of δ- and lower bounds of δ+ thus yielding subintervals of (-∞,δ+) and (δ-,0) where the above slicing applies.
Theorem 3: Let A, B, C ∈  n×n be positive definite, and let p+ and p- be defined in (10) and (11). Then is holds that
n×n be positive definite, and let p+ and p- be defined in (10) and (11). Then is holds that
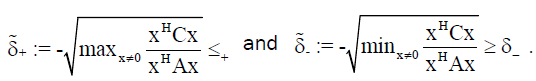 (12)
(12)
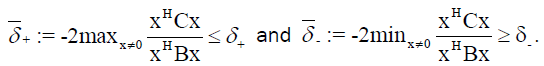 (13)
(13)
Theorem 4: Let A, B, C ∈ 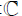 n×n be positive definite, and for
n×n be positive definite, and for 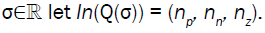
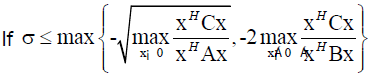
then there exists nn Eigen-values of Q(λ)x=0 in (-∞, σ).
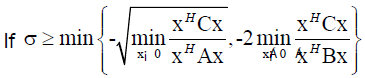
then there exists nn Eigen-values of Q(λ)x=0 in (σ, 0).
Shift Strategy
Here we consider a non-overdamped pencil (9). To this overdamped pencil we will join a corresponding hyperbolic quadratic
pencil. The hyperbolic quadratic pencil is suitable for us because it is overdamped which means for every x∈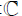 n, x≠0 a corresponding
hyperbolic quadratic pencil has two distinct real roots. Duffin in [6] has proved that the hyperbolic quadratic eigenproblem
satisfies conditions of the variational characterization of the Eigen-values.
n, x≠0 a corresponding
hyperbolic quadratic pencil has two distinct real roots. Duffin in [6] has proved that the hyperbolic quadratic eigenproblem
satisfies conditions of the variational characterization of the Eigen-values.
Let 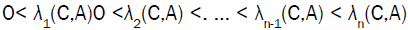 Eigen-values of the Eigen-value problems
Eigen-values of the Eigen-value problems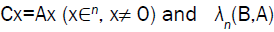 is
maximal Eigen-value of the Eigen-value problems Bx=Ax (x∈
is
maximal Eigen-value of the Eigen-value problems Bx=Ax (x∈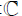 n, x≠ 0).
n, x≠ 0).
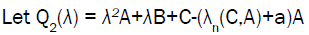 (14)
(14)
Be a quadratic pencil where 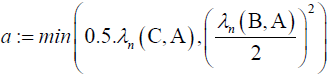
Theorem 5: Quadratic pencil (14) is hyperbolic.
Proof: It is clearly seen from the definition of quadratic pencil that matrices A, B and C-(λn(C,A)+a) A are Hermitian matrices.
By using 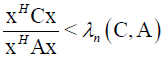 and a>0 we get
and a>0 we get 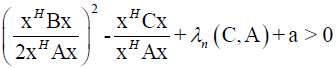 which means that our pencil is hyperbolic.
which means that our pencil is hyperbolic.
Appropriate functional for our hyperbolic pencil (14) are:
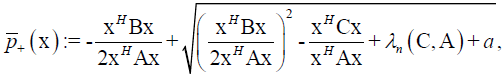 (15)
(15)
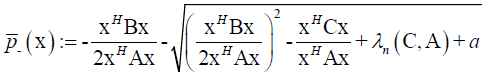 (16)
(16)
The ranges 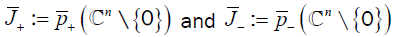 are disjoint real intervals with
are disjoint real intervals with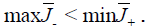
Theorem 6: Let 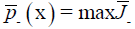 then for every
then for every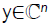 for which
for which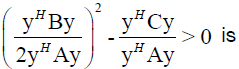
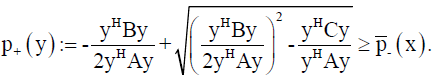 (17)
(17)
Proof: Suppose the contrary that exists y∈Cn for which 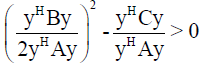 for which
for which
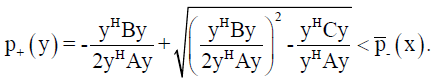 (18)
(18)
i.e.
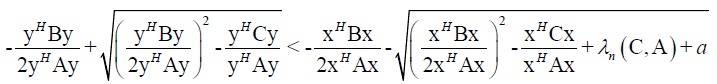
From this follows
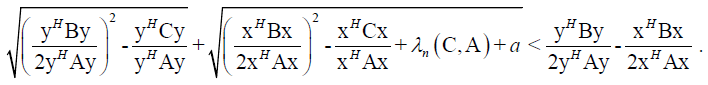 (19)
(19)
If
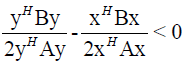
We get a contradiction. Because of this we take that
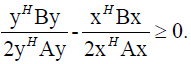
After squaring (19) and editing we get
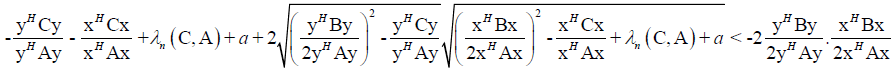 (20)
(20)
Now we have two cases
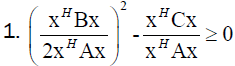
From (20 follows
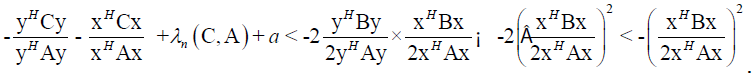
It follows
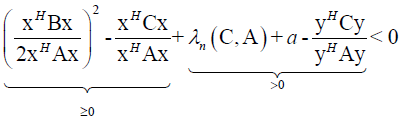 ,which is contradiction, so Theorem 6 stands.
,which is contradiction, so Theorem 6 stands.
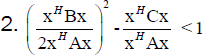
From (20) follows
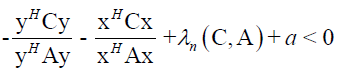 (21)
(21)
We have here two cases
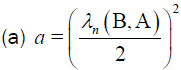
From (21) follows
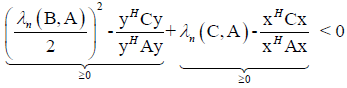 ,Which is contradiction, so Theorem 6 stands.
,Which is contradiction, so Theorem 6 stands.
(b) a = 0.5.λn (C, A) We have here two cases
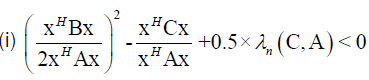
From
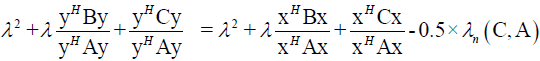 and (18) follows
and (18) follows
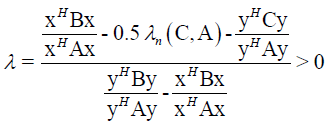 (22)
(22)
From (22) and 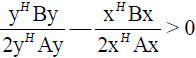 follows
follows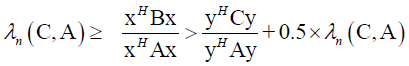
So, it follows 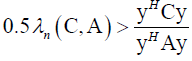
By using from 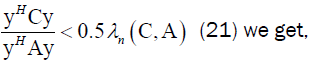
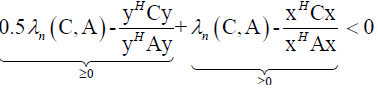
which is contradiction, so Theorem 6 stands.(ii)
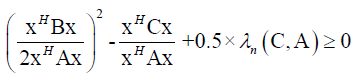
From (20) follows
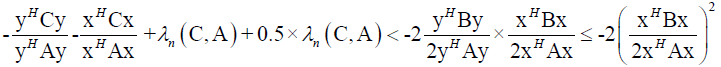
It follows
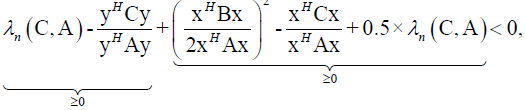
Which is contradiction, so Theorem 6 stands.
In this way we get the following improvement of the Theorem 7 and the Theorem 8.
Theorem 7: Let A, B, C ∈ 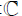 n×n be positive definite, and let p+ and p- be defined in (10 and (11. Then is holds that
n×n be positive definite, and let p+ and p- be defined in (10 and (11. Then is holds that
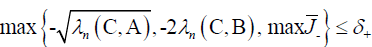
and

Next example illustrates that with the Theorem 7 we get a better lower boundary + than with Theorem 3.
Example: Quadratic pencil
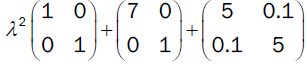 is non-overdamped. This quadratic pencil has two complex Eigen-values
-0.5002+2.1794i and -0.5002-2.1794i.
is non-overdamped. This quadratic pencil has two complex Eigen-values
-0.5002+2.1794i and -0.5002-2.1794i.
This pencil has Eigen-value of negative type -6.1926 and Eigen-value of a positive type -0.807.
Corresponding hyperbolic pencil is 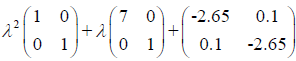
applying Theorem 3 we get lower boundary -2.2583 for δ+. By applying Theorem 7 we get lower boundary -2.2027 for δ+. Since we obtained bigger lower boundary we got an improvement.
Theorem 8: Let A, B, C ∈ 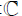 n×n be positive definite, and for σ∈
n×n be positive definite, and for σ∈  et In (Q (σ)) = (np, nn, nz).
et In (Q (σ)) = (np, nn, nz).
If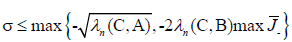
Where 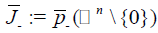 then there exists nn Eigen-values of Q (λ) x=0 in (-∞,σ).
then there exists nn Eigen-values of Q (λ) x=0 in (-∞,σ).
If 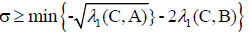
Then there exists nn Eigen-values of Q (λ) x=0 in(σ,0).
In this paper, we considered a special class of the quadratic Eigen-value problems, non-overdamped problems. The nonoverdamped problems are often seen in practice. Although the non-overdamped problems are seen in practice, because of the mathematical difficulty of this problem they are not often a subject of the research. This was motivation for their wider consideration. The overdamped problems are difficult for the consideration because the variational characterization can only partly be applied on them. Because of this in literature exists upper bound of δ+. I this paper we considered the improvement of the lower bound of δ+. We introduced completely new strategy for the determination of better lower bound of δ+. This strategy is based in the obtaining additional information from the conveniently chosen hyperbolic Eigen-value problem. In the further research we will try to improve upper bound of δ-.