Simultaneous Facial Feature Tracking and Facial Expression Recognition via Gabor Wavelet

Abstract

Facial feature tracking and facial actions recognition from image sequence involved great awareness in computer vision field. In this paper, Facial activities are describe by three levels: primary, in the base level, facial element points about each facial component, i.e., eyebrow, mouth, etc, capture the full face outline information; next, in the center level, facial action units (AUs), clear in Facial Action Coding method, represent the contraction of a specific set of facial muscles, i.e., lid tightener, eyebrow raiser, etc; to finish, in the top level, six prototypical facial expressions represent the overall facial muscle movement and are usually used to describe the human emotion state. this paper introduces a joined probabilistic structure based on the Dynamic Bayesian network (DBN) to simultaneously and logically represent the facial evolvement in different levels, their interactions and their observations. Advanced machine learning methods are introduced to learn the model based on both training data and subjective prior knowledge. Given the model and the measurements of facial motions, all three levels of facial activities are simultaneously recognized through a probabilistic inference. Extensive experiments are performed to illustrate the feasibility and effectiveness of the proposed model on all three level facial activities.

Keywords

Simultaneous Tracking and Recognition, Facial Feature Tracking, Facial Action Unit Recognition, Expression Recognition and Bayesian Network.

INTRODUCTION

The improvement of facial activities in image sequences is an important and challenging problem. Nowadays, many computer vision techniques have been proposed to characterize the facial activities in different levels: First, in bottom level, facial feature tracking, which usually detects and tracks prominent landmarks surrounding facial components (i.e., mouth, eye), captures the detailed face shape information; Second, facial actions recognition, i.e., recognize facial action units (AUs) defined in FACS, try to recognize some meaningful facial activities. The facial feature tracking and facial action units (AUs) recognition are interdependent problems. For example, the tracked facial feature points can be used as features for AUs recognition, and the accurately detected AUs can provide a prior distribution of the facial feature points. However, most current methods regularly track or recognize the facial activities separately, and ignore their interactions. In addition, the image measurements of each level are always uncertain and ambiguous because of noise, occlusion and the imperfect nature of the vision algorithm. In this paper, we build a prior model based on Dynamic Bayesian Network (DBN) to systematically model the interactions between different levels of facial activities. In this way, not only the AU recognition can benefit from the facial feature tracking results, but also the AU recognition can help improve the feature tracking performance. Given the image measurements and the proposed model, different level facial activities are recovered simultaneously through a probabilistic inference.

Some previous works combined facial feature tracking and facial actions recognition, e.g.,. However, most of them perform tracking and recognition separately, i.e., the tracked facial points are the features for the recognition stage. Fadi et al. and Chen & Ji improved the tracking performance by involving the recognition results. However, in they only model six expressions and they need to retrain the model for a new subject, while in, they represented all upper facial action units(AUs) in one vector node and in such a way, they ignored the semantic relationships among AUs, which is a key point to improve the AU recognition accuracy.

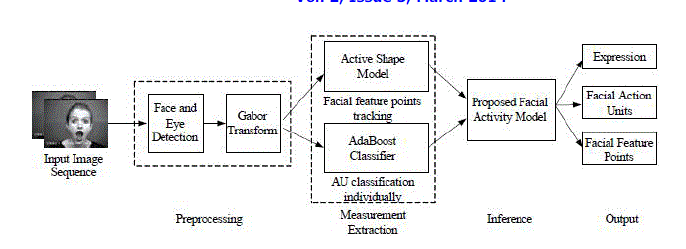
The proposed facial activity recognition system consists of two main stages: offline facial activity model construction and online facial motion measurement and inference. Specifically, using training data and subjective domain knowledge, the facial activity model is constructed offline. During the online recognition, as shown in Fig. 1, various computer vision techniques are used to track the facial feature points, and to get the measurements of facial motions (AUs). These measurements are then used as evidence to infer the true states of the three level facial activities simultaneously. The paper is divided as follows: In Sec. II, we present a brief reviews on the related works on facial activity analysis; Sec. III describes the details of facial activity modeling,

FACIAL ACTIVITY MODELING

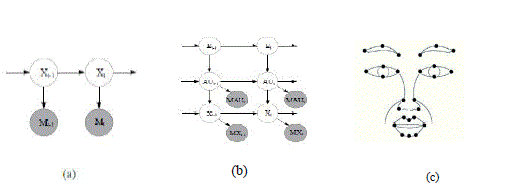
Overview of the Facial Activity Model: The graphical representation of the traditional tracking model, i.e., Kalman Filter, is shown in Fig. 2(a), where Xt is the hidden state, i.e., facial points, we want to track and Mt is the current image measurement. The traditional tracking model only has one single dynamic P(Xt|Xt-1) and this dynamic is fixed for the whole sequence. But for many applications, we hope that the dynamics can switch according to different states. Therefore, researchers introduce a switch node to control the underling dynamic system. Following this idea, we introduce the AUt node, which represents a set of AUs, above the Xt node, as shown in Fig. 2(b)(Fig. 2(b) is a graphical representation of the causal relationship of the proposed tracking model). For each state of AUt node, there is a specific transition parameter P(Xt|Xt-1,AUt) to model the dynamics between Xt-1 and Xt. In addition, the detected AUt can provide a prior distribution for the facial feature points, which is encoded in the parameter P(Xt|AUt). Given the image measurement MAU1:t and MX1:t, the facial feature points and AUs are tracked simultaneously through maximizing the posterior probability.

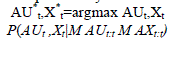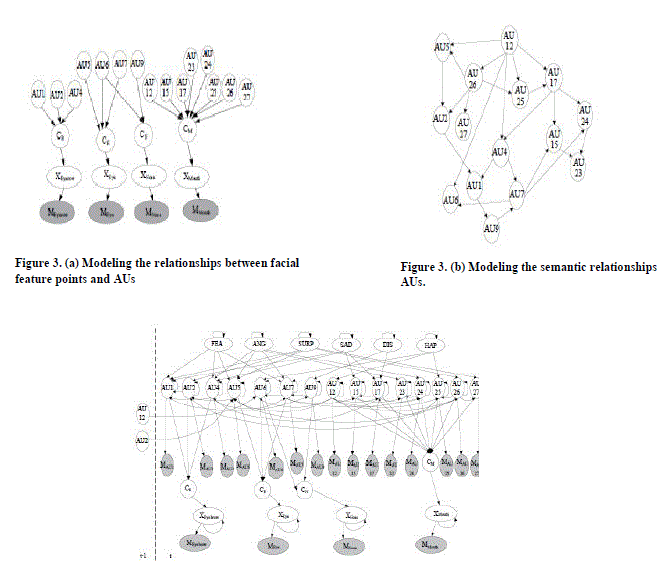
Modeling the Relationship between Facial Feature Points and AUs: In this work, we are going to track 26 facial feature points as shown in Fig. 2(c) and 14 AUs, i.e., AU1 2 4 5 6 7 9 12 15 17 23 24 25 27. Since the movement of each facial component is independent, i.e., whether the mouth is open will not affect the eyes’ movement, we model each facial component locally. Take Mouth for example, we use a continuous node XMouth to represent 8 facial points around mouth, and link AUs that control mouth movement to this node. However, directly connecting all related AUs to one facial component would result in too many AU combinations, most of which rarely occur in daily life. As a result, we introduce an intermediate node, i.e., “Cm” to model the correlations among AUs and to reduce the number of AU combination. Fig. 2(a) shows the modeling for the relationships between facial feature points and AUs for each facial component.

Each AU has two discrete states which represent the “presence/absence” states of the AU. The modeling of the semantic relationships among AUs will be discussed in the later section. The intermediate nodes(i.e. "CB", "CE", "CN" and "CM") are discrete nodes, each state of which represents a specific AU/AU combination related to the face component. The number of states of each intermediate node P(Ci|pa(ci)) are set manually based on the data analysis.The facial feature point nodes (i.e., XEyebrow,XEye, XNose and XMouth) have continuous state and are represented by continuous shape vector. Give the local AUs, the Conditional Probability Distribution (CPD) of the facial feature points can be represented as a Gaussian distribution, i.e., for mouth:

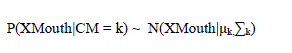With the mean shape vector μk and covariance matrix, Σk

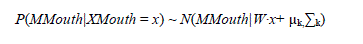With the mean shape vector μk,, regression matrix W, and covariance matrix Σk. These parameters can be learned from training data.

Modeling the Relationships among AUs: Detecting each AU statically and individually is difficult due to image uncertainty and individual difference. Following the work in, we employ a BN to model the semantic relationships among AUs. The true state of each AU is inferred by combining the image measurements and the probabilistic model. Cassio et al. developed a Bayesian Network structure learning algorithm which is not dependent on the initial structure and guarantee a global optimality with respect to BIC score. In this work, we employ the structure learning method to learn the dependencies among AUs. To simplify the model, we use the constraints that each node has at most two parents. The learned structure is shown in Fig. 2(b).

Modeling the Dynamics: In the above sections, we have modeled the relationships between AUs and facial feature points, and the semantic relationships among AUs. Now we extend the static BN to a dynamic BN(DBN) to capture the temporal dependencies. For each facial point node, i.e., for mouth, we link the node at time t – 1 to time t to denote the self dynamics, which depicts the facial feature point’s evolvement in time. For AUs, beside the self dynamics, we also link AUi at time t − 1 to AUj ; j ≠ I at time t, to capture the temporal dependency between AUi and AUj . Based on the analysis of the database, we link AU12 and AU2 at time t−1 to AU6 and AU5 at time t, respectively to capture the dynamic dependency between different AUs. Fig. 2(c) gives the whole picture of the dynamic BN, including the shaded visual measurement nodes. For presentation clarity, we use the self-arrows to indicate the self dynamics as described above.

LEARNING AND INFERENCE

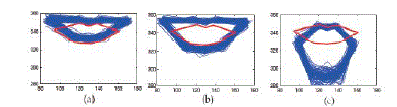
DBN Parameter Learning: Give the DBN structure and the definition of the CPDs, We need to learn the parameters from training data. In this learning process, we manually labeled the AUs and facial feature points in the Cohn and Kanade DFAT-504 database (C-K db) frame by frame. These labels are the ground-truth states of the hidden nodes. The states of the measurement nodes are obtained by various image-driven methods. We employ a facial feature tracker which is based on the Gabor wavelet matching and active shape model(ASM) to track the facial feature measurements. For AUs, we apply an AdaBoost classifier based on Gabor feature to obtain the measurement for each AU. Based on the conditional independencies encoded in DBN, we learn the parameters individually for each local structure. For example, for mouth, we learn the parameters P(XMouth|CM) and P(MMouth|XMouth) from labels and measurements. Fig 4 shows the 200 samples draw from the learned CPDs of the”Mouth” node: P(XMouth|CM) (the red curve is the neutral constant shape). We can see that, given different AUs, the distribution of facial feature points is different. Thus, the AUs actually can provide a prior distribution for facial feature points.

DBN Inference: Given the DBN model, we want to maximize the posterior probability of the hidden nodes as Eq. 1. In our problem, the posterior probability can be factorized and computed via the facial activities model by performing the DBN updating process as described in. Then, the true facial feature points and AUs states are inferred simultaneously over time by maximizing

P(AUt;Xt|MAU1:t;MX1:t).

EXPERIMENTS

The proposed model is evaluated on Cohn and Kanade DFAT-504 database (C-K db), which consists of more than 100 subjects covering different races, ages, and genders. We collect 308 sequences that contain 7056 frames from the C-K database. We divide the data into eight folds and use leave-one-out cross validation to evaluate our system. The experiment results for each level are as follows:

Facial Feature Tracking: We tracked the facial feature point measurements through an active shape model (ASM) based approach, which first searches each facial feature point locally and then constrains the feature point positions based on the trained ASM model. This approach performs well when the expression changes slowly and not significantly, but may fail when there is a large and sudden expression change. At the same time, our model can detect AUs accurately, especially when there is a large expression change. The accurately detected Aus provide a prior distribution for the facial feature points, which help to infer the true point position. To evaluate the performance of the tracking method, the distance error metric is defined per frame as

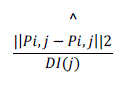where DI (j) is the interocular distance measured at frame j, pi,j is the tracked position of point i, and is the labeled position. By modeling the interaction between facial feature points and AUs, our model improves the average facial feature point measurement error from 3.00 percent to 2.35 percent, an relative improvement of 21.67 percent. Table 1 shows a comparison of tracking the facial feature points by using the baseline method, and the proposed model for each face component, respectively.

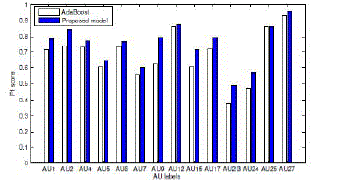
Facial Action Recognition: Figure 5 shows the performance for generalization to novel subjects in C-K database by using AdaBoost classifier along and using the proposed model, respectively. The AdaBoost classifier achieves an average F1 score (a weighted mean of the precision and recall) of 0.6805 for the 14 target AUs. With the use of the proposed method, our system achieves an average F1 score of 0.7451. We get an improvement of 9.49 percent by modeling the semantic and dynamic relationships among AUs and the interactions between AUs and facial points. Previous works on AU recognition usually report results using classification rate, which is less informative when data is unbalanced, i.e., C-K db. Hence, we report the results using both classification rate and F1 score. Table 2 summarizes the comparison of the proposed model with some early sequence-based approaches, and we can see that our method gets a better result compared to the state-of-the-art methods.

CONCLUSION

In this paper, we proposed a prior model based on DBN for simultaneously facial activities tracking and recognition. By modeling the interactions between facial feature point and AUs and the semantic relationships among Aus, the proposed model improves both facial feature points tracking and Aus recognition over the baseline method.

Tables at a glance

Table 1

Figures at a glance

Figure 1 Figure 2 Figure 3 Figure 4 Figure 5

References

Y. Bar-Shalom and X. Li. Estimation, Tracking: Principles, Techniques, and Software. Hardcover, Artech House Publishers, 1993. J. Chen and Q. Ji. A hierarchical framework for simultaneous facial activity tracking. 9th Intl Conf. FG, 2011. C. P. de Campos and Q. Ji. Efficient structure learning of bayesian networks using constraints. Journal of Machine Learning Research, 12:663–689, 2011. P. Ekman and W. V. Friesen. Facial Action Coding System (FACS): Manual. Consulting Psychologists Press, 1978