Skew and Slant Angles of Handwritten Signature

L. B. Mahanta; Alpana Deka

Skew and Slant Angles of Handwritten Signature

L. B. Mahanta¹, Alpana Deka²

Associate Professor - I, Institute of Adv. Study in Science and Technology, Guwahati – 35, P.O- Gorchuk Assam, India
Research Scholar,Department of Statistics,Gauhati University,Guwahati-14, Assam, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

For any signature verification system, detection and correction of skew and slant angles are two important factors in preprocessing stage. To make an efficient verification system, the input signature image should be perfectly preprocessed as far as possible so that we can properly extract the required features. In correction of skew angle, attempt is made that word orientation of the signature is parallel to horizontal direction. On the other hand, in slant angle correction, operations are performed to make all the vertical strokes erect [1]. This paper presents three different approaches for detection of a signature’s skew angle. Also it is explained how a slant angle can be detected and corrected.

Keywords

skew angle; slant angle; projection profile; center of gravity;

INTRODUCTION

Skew and Slant are two different terms relating to handwritten signature. In any handwritten signature verification system, the main aim is to find out accurate result. In order to improve performance of it, all samples of the signatures should be made normalized one. Skew detection/correction and Slant detection/correction are important perspectives relating to normalization of signature. Amount of skew and slant may depend on different factors like writing surface and material, physical and psychological state of a person and environmental factors etc [2].

Skew Angle: A skew occurs when baseline of a signature makes an angle to the horizontal frame [3]. Different types of skew angles of a signature can be defined as follows [4]. (A line on which a signature aligns is known as baseline.)

1. Negative Skew: In negative skew, the direction of baseline of a signature goes from bottom left to top right in a upward direction. Then the angle made by the baseline with horizontal direction of the signature will be negative skew angle as shown in Fig 1.

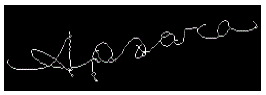Figure 1 : Negative skewed signature

2. Zero Skew: When baseline is parallel to the horizontal direction, then the signature is known as zero skewed.

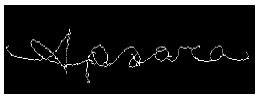Figure 2 : Zero skewed signature

In Fig 2, a zero skewed signature is shown.

3. Positive Skew: In positively skewed signature, the baseline comes from top left to bottom right in a downward direction as in Fig 3 and hence angle made by this baseline with horizontal direction is positive skewed angle.

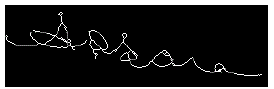Figure 3: Positive skewed signature

Slant Angle: Slant angle is the angle made by the vertical text strokes with vertical direction of a signature angle. Different kinds of slants are [4],[5]:

Negative Slant: When the angle between vertical text strokes with vertical direction is greater than 90 degrees then it is known as negative slant angle of signature. A negative slant angle is given in Fig 4.

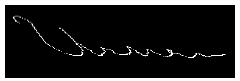Figure 4: Negative slant angle

Zero Slant: Here angle formed by vertical text strokes with vertical direction is 90 degrees.

Figure 5: Zero slant angle

Above figure (Fig 5) is an example of zero slant signature.

Positive Slant: Here angle between vertical text strokes and vertical direction is less than 90 degrees. A positive slant angled signature is given in Fig 6.

Figure 6: Positive slant angle

From the above discussion it is clear that the main difference between skew angle and slant angle is the way of angle measurement. Skew angle is measured with respect to horizontal direction whereas, slant angle is calculated vertically.

SKEW ANGLE ESTIMATION APPROACHES

Skew detection and Correction is a challenging field in handwritten signature verification system. A skew angle of a sample of signatures may vary from person to person and also may differ within the same person. Estimation of skew angle can be performed by different approaches as given below:

Projection Profile Analysis:

Skew estimation based on projection profile is a simple and straight forward approach. In horizontal projection profile technique, an M×N signature image is fed into the system to get a column vector of size M×1. Here, pixel values in each row of the signature image are extracted and finally by summing these values will give a column vector [6].

Steps for estimation of skewed signature with horizontal projection profile:

Step 1: Input a skewed signature into the system.

Step 2: Find out horizontal projection profile for the signature.

Step 3: Store maximum horizontal projection profile in a variable say U.

Step 4: Rotate the image by 5 degree.

Step 5: Repeat the steps ii) and iii) and store the value found in step iii) in a new variable say V.

Step 6: Calculate the difference between U and V.

Step 7: Rotate the signature as the value found in step vi).

Figure 7 : Skewed signature

Figure 8 : Skew remove to some extent

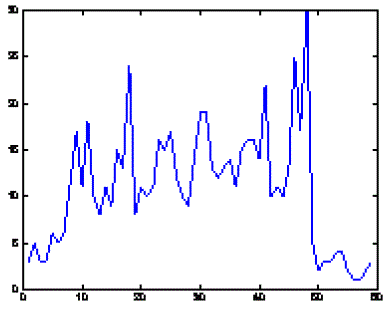Figure 9 : Horizontal projection profile of Fig 7

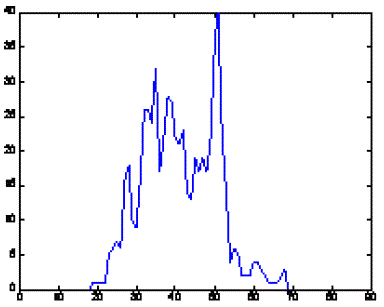Figure 10 : Horizontal projection profile of Fig 8

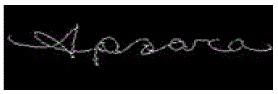Figure 11: Skew free signature.

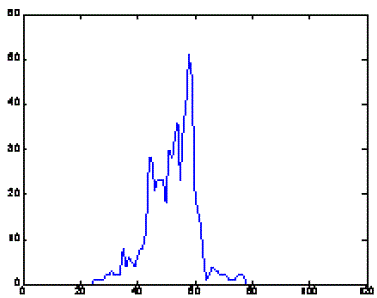Figure 12 : Horizontal projection profile of Fig 11

Skew Detection using Center of Gravity

Using the concept of center of gravity or center of mass, we can measure the skewness of a signature. The main steps for detection of skew angle are [7]:

Step 1: Divide a signature image vertically into two equal halves.

Step 2: Compute center of gravity for both left and right halves.

Step 3: Join the two centers of gravity by a line.

Step 4: Compute slope of the line.

Step 5: Calculate skew angle by taking the inverse of the slope as found in step iv).

Step 6: Rotate the signature by detected skew angle.

Figure 13: Skew angle detection using center of gravity a) Center of gravity in left half b) Center of gravity in right half c) Join the two center of gravities d) Skew free signature

Skew Detection using Radon Transform

We can also perform radon transform to detect whether a signature is skewed or not. The radon transform on a signature can be applied by adding radon transform of each pixel. Projections of an image matrix along specified directions can be computed by radon function. Here, skew angle is calculated on the basis of radon function with maximum value [8].

Figure 14 : A skewed signature.

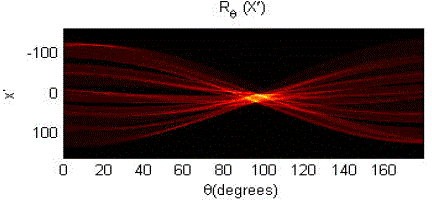Figure 15 : Radon transform applying on Fig 14.

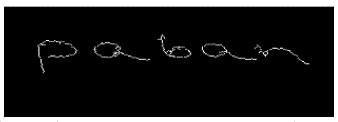Figure 16 : Skewed free signature using radon transform.

SLANT ANGLE ESTIMATION APPROACH

Slant angle detection and correction are preprocessing parts for an efficient signature verification system. In the above approaches for skew correction, we perform rotation operation but in slant correction we will perform shear transformation. Here slant correction is done with following steps [4]:

Step 1: Perform shear (vertical) transformation for few angles on the signature image.

Step 2: Find the vertical projection profile.

Step 3: The value of maximum vertical projection profile will give the slant angle.

Step 4: Perform shear transformation with the slant angle as found in step iii).

From the above table, it is clear that maximum value of vertical projection profile is 22 and its corresponding angle is 0.5. Hence 0.5 is the required slant angle. After correcting the slant angle, we will perform shear transformation on the input signature to make it zero slant angled signature.

Figure 17 : Slant signature

Figure 18 : Slant free signature

CONCLUSION

In a signature verification system, detection of skew and slant angles can be considered an important feature to detect signature variability from one person to another whereas correction of skew and slant angles may reduce signature variability within the same person [4]. In correction of skew and slant angles of a handwritten signature verification system, we try to make a signature to be zero skewed and zero slant angled respectively. To correct skew angle, we perform rotation transformation, but in correction of slant angle we perform shear transformation.

References

Suresh Chandra Satapathy, P.S. Avadhani, Ajith Abraham(Eds.), “Advances in Intelligent and Soft Computing”,Proceedings of the International Conference on Information Systems Design and Intelligent Applications, Springer, pp: 354, 2012.

T. Fotak, M. BaÃâÃÂa, P. Koruga, “Handwritten Signature Identification using Basic Concepts of Graph Theory”, Wseas Transactions on Signal Processing, Vol. 7, Issue 4, pp. 117-129, 2011.

H. Bunke, P. S. P. Wang, “Handbook of Character Recognition and Document Image Analysis”, WorldScientific, pp: 124.

Frank de Zeeuw,”Slant Correction using Histograms”, pp: 1-10, 2006.

Helmut Ploog, “Handwriting Psychology: Personality Reflected in Handwriting”, iUniverse, pp: 38-39, 2013.

Shutao Li, Qinghua Shen, Jun Sun, “Skew Detection using wavelet decomposition and projection profile analysis”, Pattern Recognition Letters, Vol. 28, pp: 555-562, 2007.

M. Blumenstein, C. K.Cheng, X. Y. Liu, “New Preprocessing Techniques for Handwritten Word Recognition”, Proceedings of the Second IASTED International Conference on Visualisation, Imaging and Image Processing, 2002.

Prakash K Aithal,Rajesh G,U Dinesh Acharya, Siddalingaswamy P.C., “A Fast and Novel Skew Estimation Approach using Radon Transform”, International Journal of Computer Information Systems and Industrial Management Applications, Vol. 5, pp: 337-344, 2013.