ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
Shalu1, Wg. Cdr. Anil Chopra2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
Privacy preserving data mining techniques helps in providing security to sensitive information from unauthorized access. Large amount of data is collected in many organizations through data mining. So privacy of data becomes the most important issue in the recent years. Several numbers of techniques such as generalization, bucketization, anonymization have been proposed for privacy preserving data publishing. Generalization loses significant amount of information especially for high-dimensional data according to recent works. Whereas bucketization does not prevent the membership disclosure and cannot applicable to data that does not have clear separation between quasi-identifiers and sensitive attributes. In this paper, we present a slicing technique to prevent generalized loses and membership disclosure. It can also handle high –dimensional data and develops efficient algorithm for computing the sliced data that obeys the ? -diversity check requirement. Slicing preserves better utility than generalization and is more effective than bucketization in workloads involving the sensitive attribute in our experiment
KEYWORDS |
| Generalization, bucketization, ̢̉̉ -diversity, slicing, data publishing. |
I. INTRODUCTION |
| Data mining is the exploration and analysis of large quantities of data in order to discover valid, novel, potentially process that plays a vital role in extraction of useful information. Today huge databases exist in various applications i.e. Medical data, census data, communication and media-related data, consumer purchase data and data gathered by government agencies etc. So data sharing is needed for full utilization of collected data because pooling of medical data can improve the quality of medical research also the data gathered by the government (e.g. census data) should be made publicly available for calculating the population of country, calculating the numbers of candidates who become eligible for voting etc. As the private information of individuals are public or distributed online so privacy become the important issue these days. For this reason various privacy preserving techniques (PPDM) are must applied with data mining algorithm so that the private information of the individual can be protected during the extraction of sensitive information in the knowledge finding process that is also known as KDD process. Micro data has received lots of attention in the recent years. Today many organizations publish their micro data. This information includes details about individual entity, organization, firm, industry, person etc. Main objective of privacy preserving data mining techniques is to modify the original data in such a way that the private information is not revealed as well as the data remains useful for the analysis purpose. Most popular techniques used for microdata anonymization are generalization and bucketization which involves various attributes. In both the approaches attributes are divided into three categories which includes identifiers, quasi-identifiers, and sensitive identifiers. Identifiers can uniquely identify an entity or individual such as Name, quasi-identifiers (QI) are not unique-identifiers itself but when we combine them together we can create unique –identifier e.g. age, zip code, sex etc., sensitive attributes(SA)are which unknown to data miners or adversaries and treated as sensitive e.g. salary , disease. The difference between both the techniques is that in bucketization QI attributes are not generalized whereas generalization replaces quasi-identifier values with values that are less-specific but remains semantically consistent so that the tuples in the same bucket cannot be identified on the basis of the quasi-identifiers. In bucketization SAs values are separated from QIs values by randomly permuting the SA values in each bucket. The anonymized data consist of a set of buckets with the distinct ordering of sensitive attribute values. But both the techniques are not efficient in preserving private data such salary, disease, treatment etc. So, we proposed the technique slicin3g for preserving private information of individuals and publishing that information by slicing the data both horizontally and vertically. Data slicing can also be used to prevent membership disclosure and is efficient for high dimensional data and preserves better data utility. |
II. RELATED WORK |
| In [1] author proposed a new anonymization method that is data slicing for privacy preserving and data publishing. Data Slicing overcomes the limitations of generalization and bucketization and preserves better utility while protecting the sensitive information. Slicing of the data is a novel technique for handling high dimensional data and data without clear separation between QIs and SAs. By preserving correlations between the highly correlated attributes privacy is protected. |
| In [5] author discussed about the detailed survey on various anonymization methods each have their own significance. Generalization causes too much of information loss and bucketization fails in privacy preservation due to membership disclosure. Slicing performs better than bucketization, generalization and many other anonymization methods. Slicing handles high dimensional data by partitioning the attributes in columns and thus helps in protecting the private information Thus slicing in combination with correlation analysis has the high data utility and preserves the privacy. In [2] author introduces a new approach slicing which partitions attributes so that highly correlated attributes are in the same column. In case of data utility, grouping highly correlated attributes helps in breaking the correlations among those attributes. In case of privacy, the association of uncorrelated attributes values is much less frequent and thus more identifiable because the association of uncorrelated attributes presents higher identification risks than the association of highly correlated attributes. Thus it is good to break the associations between uncorrelated attributes so that the private information is protected. |
III SLICING TECHNIQUES |
| We introduce a Slicing algorithm so that we can achieve ̢̉̉ -Diverse slicing of data. In our implementation work, we assume the micro data table T and two parameters c and ̢̉̉, and then algorithm computes the sliced data table consisting of c columns which satisfy the privacy requirements of ̢̉̉-diversity. This algorithm consists of three phases: attribute partitioning, column generalization, and tuple partitioning. We now describe the three phases. |
A. Attribute Partitioning |
| Slicing first partitions the attributes of original micro data table T in to columns. Partitioning is done vertically so the column contains a subset of attributes. Partitioning is also done horizontally which divides the tuples in to buckets where each bucket contains a subset of tuples. After partitioning, highly correlated attributes appears in the same column. It is good for both utility and privacy. In terms of data utility, grouping highly correlated attributes preserves the correlations among those attributes. In terms of privacy, the association of uncorrelated attributes presents higher identification risks than the association of highly correlated attributes because the associations of uncorrelated attribute values is much less frequent and thus got the high probability to get identified. |
B. Column Generalization |
| Column generalization may be required for preserving identity/membership disclosure. If a column value is unique in a column, a tuple with this unique column value can only have one matching bucket. And this is not good for privacy protection because adversaries can easily identify this unique column value. So in this case, it would be useful to apply column generalization to ensure that each column value appears with at least some frequency. |
Algorithm 1 |
Algorithm tuple-partition (T, ̢̉̉) |
| 1. Q = {T}; SB = φ |
| 2. while Q is not empty |
| 3. remove the first bucket B from Q; Q = Q − {B} |
| 4. split B into two buckets B1 and B2, as in Mondrian |
| 5. if diversity-check(T, Q ∪ {B1,B2} ∪ SB, âÃâÃâ) |
| 6. Q = Q ∪ {B1, B2} |
| 7. else SB = SB ∪ {B} |
| 8. return SB. |
C. Tuple Partitioning |
| In this phase, tuples are partitioned in buckets. Mondrian[3] method is used for partitioning tuples in to buckets. First algorithm used in slicing is the tuple-partitioning algorithm mentioned in Algorithm 1.Tuple-partitioning algorithm maintains two data structures: 1) a queue of buckets Q and 2) a set of sliced buckets SB. Initially, Q contains only one bucket which includes all tuples and SB is empty. In each iteration, the algorithm removes a bucket from Q and splits the bucket into two buckets [5]. If the sliced table after the split satisfies ̢̉̉ -diversity, then the algorithm puts the two buckets at the end of the queue Q Otherwise, we cannot split the bucket anymore and the algorithm puts the bucket into SB (7). When Q becomes empty, we have computed the sliced table. The set of sliced buckets is SB (8). |
Algorithm1.1 |
Algorithm diversity-check (T, T*, ̢̉̉) |
| 1. for each tuple t ∈ T, L[t] = φ |
| 2. for each bucket B in T* |
| 3. record f(v) for each column value v in bucket B |
| 4. for each tuple t ∈ T |
| 5. calculate p(t,B) and find D(t,B) |
| 6. L[t] = L[t] ∪ {(p(t,B),D(t,B))} |
| 7. for each tuple t ∈ T |
| 8. calculate p(t, s) for each s based on L[t] |
| 9. if p(t, s) ≥ 1/âÃâÃâ, return false |
| 10. return true. |
| The main part of the tuple-partition algorithm is to check whether a sliced table satisfies „âÃâÃâ -diversity (5) mentioned in Algorithm 1.Now Algorithm1.1 gives a description of the diversity-check algorithm. For each tuple t, the algorithm maintains a list of statistics L[t] about tâÃâ¬ÃŸs matching buckets. Each element in the list L[t] contains statistics about one matching bucket B: the matching probability p (t, B) and the distribution of candidate sensitive values D(t,B). The algorithm first takes one scan of each bucket B (2 to 3) to record the frequency f (v) of each column value v in bucket B. Then, the algorithm takes one scan of each tuple t in the table T ( 4 to 6) to find out all tuples that match B and record their matching probability p(t, B) and the distribution of candidate sensitive values D(t,B)which are added to the list L[t] ( 6). At the end of line 6, we have obtained, for each tuple t, the list of statistics L[t] about its matching buckets. A final scan of the tuples in T will compute the p (t,s) values based on the law of total probability stated below: |
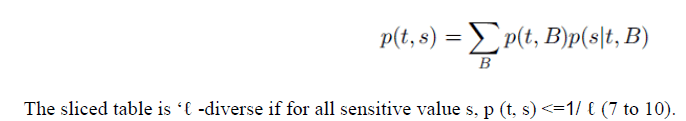 |
IV IMPLEMENTATION WORK |
STEPS INVOVLED IN SLICING PROCESS |
| 1. Original Data |
| 2. Generalized Data |
| 3. Bucketized Data |
| 4. Multiset-based Generalization Data |
| 5. One-attribute-per-Column Slicing Data |
| 6. Sliced Data |
1. Original Data |
| We have entered the data in the terms of name, password, email, mobile number, date of birth, age, gender, zip code etc. in our database of various patients. After entering all the data of various patients by admin, records are stored in database as shown below in the table1.1. |
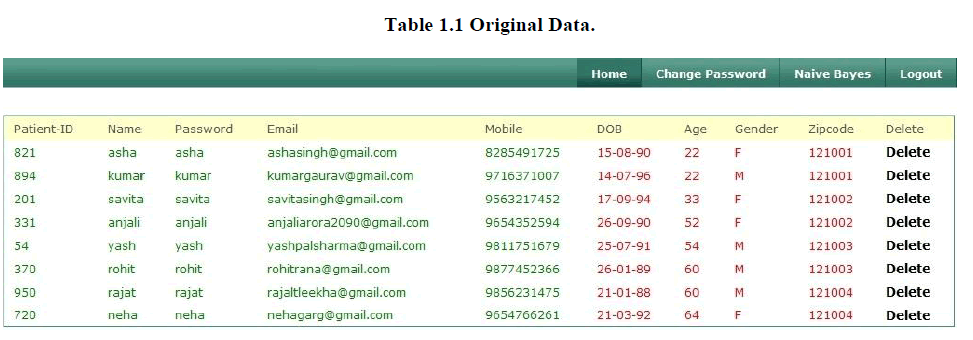 |
2. Generalized Data |
| Then we generalized data, in order to perform data mining tasks. . In generalization approach we use the identifiers data and Quasi Identifiers. Here the attribute age is identifiers, and gender, zipcode is quasi identifiers. Here we generalized the attributes zip code, gender and age. It prevents the identification of individual records in the data and the data of dataset are stored into two buckets. But this significantly reduces the data utility of the generalized data. |
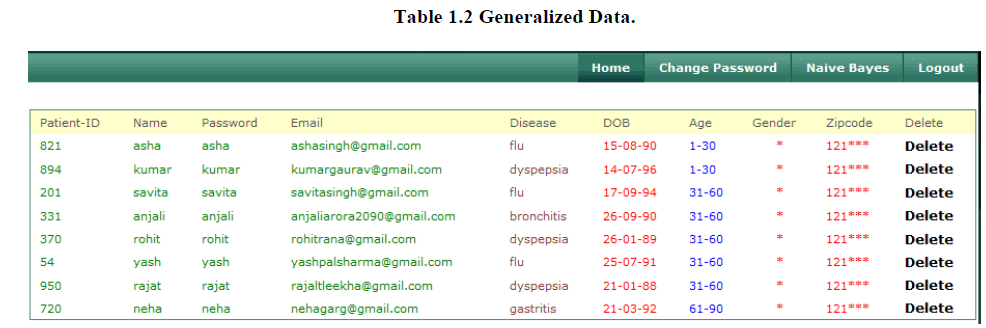 |
3. Bucketized Data |
| Our implemented work shows the effectiveness of slicing in membership disclosure protection. Here we perform the 2- diversity process. Our work also compares the number of matching buckets for original tuples and we bucketized the data on the basis of the subset of original table such that each tuple belongs to exactly one subset. Each subset of tuples is called a bucket. Here we bucketized the data on the basis attribute disease, gender and zipcode in one bucket. Our results show that bucketization does not prevent membership disclosure as almost every tuple is uniquely identifiable in the bucketized data. So we need to perform multiset-based generalization on data. |
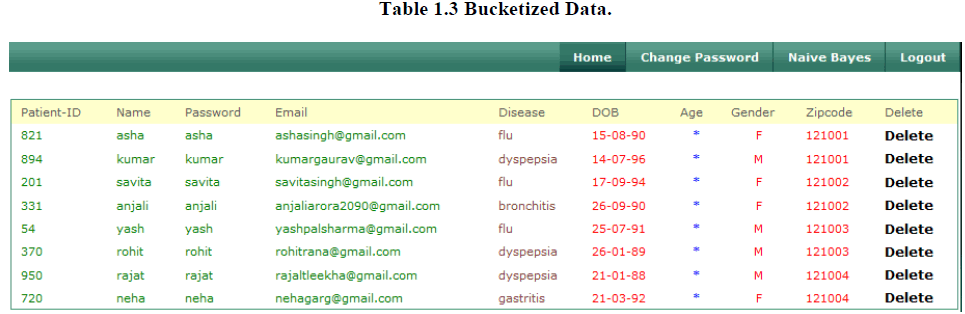 |
4. Multiset-based Generalization Data |
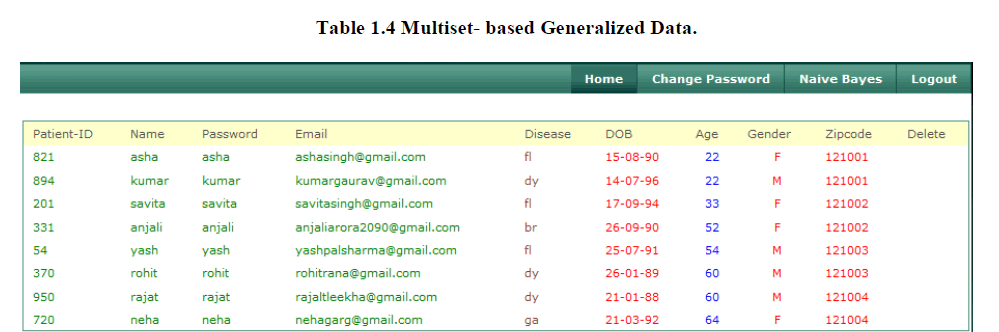
| Our works observe that this Multiset-based generalization is equivalent to a trivial slicing scheme where each column contains exactly one attribute, because both approaches preserve the exact values in each attribute but break the association between them within one bucket. Here we modified the value of “Disease “attribute in thus break the association between the one bucket. |
 |
5. One-attribute-per-Column Slicing Data |
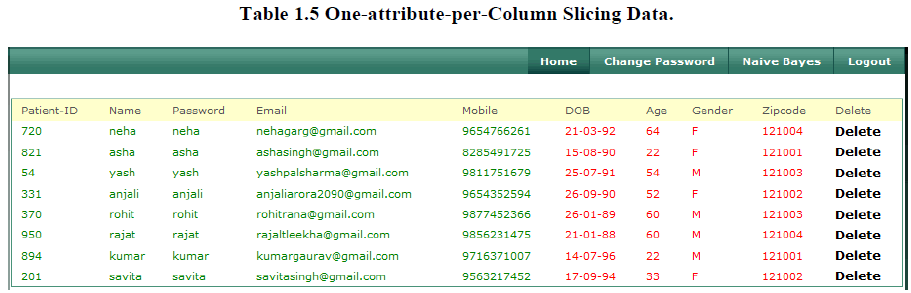
| Our works observe that while one-attribute-per-column slicing preserves attribute distributional information, it does not preserve attribute correlation, because each attribute is in its own column. For example, in the sliced table shown in Table 1.5 below correlations between Age and gender and correlations between Zip code and Disease are preserved. In fact, the sliced table encodes the same amount of information as the original data with regard to correlations between attributes in the same column. |
 |
6. Sliced Data |
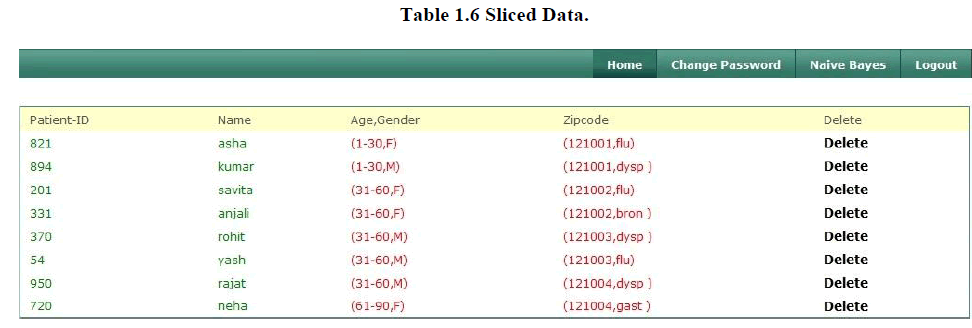
| Slicing can handle high-dimensional data. By partitioning attributes into columns, slicing reduces the dimensionality of the data. Each column of the table can be viewed as a sub-table with a lower dimensionality. Here in table1.6 attribute partition is {age gender}, {Zip code, Disease} and tuple partition is ({t1, t2, t3, t4}, {t5, t6, t7, t8}). Consider tuple t1 with QI values (22, M, 121001) In order to determine t1âÃâ¬ÃŸs sensitive value, one has to examinet1âÃâ¬ÃŸs matching buckets. By examining the first column (Age, Gender) in Table 1.6, we know that t1 must be in the first bucket B1 because there are no matches of (22, M) in bucket B2. Therefore, one can conclude that t1 cannot be in bucket B2 and t1 must be in bucket B1.Then, by examining the Zip code attribute of the second column (Zip code, Disease) in bucket B1, we know that the column value for t1 must be either (121001, dyspepsia) or (121001, flu) because they are the only values that match t1âÃâ¬ÃŸs zip code 121001. Note that the other two column values have zip code 121002. Without additional knowledge, both dyspepsia and flu are equally possible to be the sensitive value of t1. Therefore, the probability of learning the correct sensitive value of t1 is bounded by 0.5. Similarly, we can verify that 2-diversity is satisfied for all other tuples in Table 1.6. |
 |
V. CONCLUSION AND FUTURE WORK |
| This paper presents a novel approach slicing for privacy preserving microdata publishing. It is better than various data anonymization techniques. We illustrate how to use slicing for privacy threats shown by generalization and bucketization. Our implementation work shows that slicing overcomes the limitations of generalization and bucketization and preserves better utility while protecting against privacy threats. Slicing is also capable for handling high-dimensional data. By partitioning attributes into columns and then each column of the table can be viewed as a subtable with a lower dimensionality. We protect privacy by breaking the association of uncorrelated attributes and preserve data utility by preserving the association between highly correlated attributes. The ̢̉̉ -diversity slicing check algorithm provides secure data. As several number of anonymization techniques have been designed, problem still persist that how to use the anonymized data. In our experimented work, we randomly generate the associations between column values of a bucket. Which may lose data utility. So it gives us a future direction is to design the data mining tasks using the anonymized data provided by the anonymization techniques which gives the better data utility. |
References |
|