1Department of Mathematics, Bellary Institute of Technology and Management, Bellary, Karnataka, India
2Department of Mathematics, Gulbarga University, Gulbarga, Karnataka, India
Received date: 24/11/2015; Accepted date: 28/12/2015; Published date: 03/01/2016
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
The question of determining metric spaces which have the property that every continuous self-map on it has a periodic point is considered. It is settled completely among zero-dimensional spaces (Theorem -1) and also among all sunsets of R (Theorem-2).
Metric spaces, Periodic points properties (p.p.p)
The concept of periodic points has been well-studied in the Theory of Functions [1,2], Ergodic Theory [3], Theory of Fractals [4], Theory of Dynamical Systems [5-7] and Algebraic Topology [8]. A topological space X has a periodic point. This is analogous to the fixed point property [9] that has been well-studied.
The results in this paper improve the results of Saradhy [10]. Some of these results have been used by him to obtain analogues of Sarkovski’s theorem.
First, it is found that the study of p.p.p. leads to the class of countable compact spaces. It is already known that every countable compact metricspace X has p.p.p.[11]. It follows that every closed subspace of such X also has p.p.p. It is then necessary to examine whether the converse is true, i.e. if a metric space X has the property that every closed space of X has p.p.p, then X should be countable and compact. This is answered in affirmative. This may be compared with the main result of [12] where a similar converse to Banach’s contraction mapping theorem has been proved. The only result on countable compact spaces that is needed for the present discussion, has been proved by Mazurkiewicz and Sierpinski [13] and in a different way Kanna [14]. It states that every countable compact space is a well-ordered space.
N denotes the set of all natural numbers. Let f: X → X be any self-map of X.
A point x is called a periodic point of f if f n (x) = x for some n in N. Here f n is the n-fold composite of f. If this happens with n=1, then it is called a fixed point off. Two simple proposition are presented below:
Proposition: The following spaces satisfy p.p.p.
(a). All finite spaces.
(b). All compact convex subsets of R′′; in particular the closed interval [0,1] in R and the closed unit disc D in R2,
(c). All strongly rigid spaces (defined in the proof that follows) and
(d). All well-ordered compact spaces, and in particular [1, Ω], where Ω is the first uncountable ordinal number.
Proof: (a). Let X be a finite space having exactly n elements, Let f: X → X be any function. Let x0 ∈ X. There should exists r, s with f r (x0) = f s (x0 ), and r<s. Then f r (x0) is a periodic point of f.
(b). It is well-known theorem that every compact convex of R′′ has the fixed point property (f.p.p), namely that every continuous self-map has a fixed point [9] If is easily seen that f.p.p implies p.p.p.
(c). A Hausdorff space X is said to be strongly rigid if every continuous self-map of X is either a constant map or the identity map. Obviously, these spaces have f.p.p and therefore p.p.p.
(d). Let X be well-ordered compact space and let f: X → X be continuous. By Birkhoff’s theorem [15], (X, f) contains a minimal subsystem (Y, f / Y). If y0 is the least element of Y, then y0 is both recurrent (because Y is minimal) and isolated (because Y is well-ordered) and therefore periodic.
Proposition-2: The following spaces do not possess p.p.p.
(a) Any infinite discrete space,
(b) The circle S1,
The infinite product 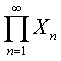 of finite spaces X n = {1,2,....,n} and therefore the Cantor Set K (known to be homeomorphic to it )
of finite spaces X n = {1,2,....,n} and therefore the Cantor Set K (known to be homeomorphic to it )
The real line R (and more generally any topological group with an element of infinite order) and (e). The Stone-Cech compactification β N of the discrete space N of natural numbers.
Proof: (a) If X is an infinite discrete space, let A = {x1, x2,……, xn…} be a countably infinite subset of X. Define f: X → X by
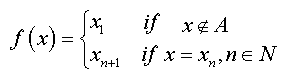
Then f is a continuous self-map of X without any periodic point.
b). Let S' = { (x, y)∈ R2 : x2 + y2 = 1}. Let θ be an angle that is not a rational multiple of π. Then the rotation θ radians (this is same as multiplication by the complex number exp (iθ ) if S1 is viewed in the complex plane) is a continuous self-map of S1 without periodic points.
(c). Let for every n in N, the set Xn be equal to {m ∈ N: m ≤ n}. Provide discrete topology to each Xn. Let 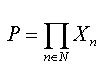 with the product topology. Consider f: P → P defined by the rule. If x = (xn) ∈ P, then f ( x ) = y whose nth coordinate yn is given by
with the product topology. Consider f: P → P defined by the rule. If x = (xn) ∈ P, then f ( x ) = y whose nth coordinate yn is given by
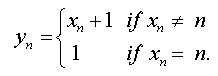
In other words we are taking a cyclic permutation pn: X n→ X n of order n for each n in N and 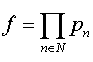 . The component functions f n: P → X n have the property that
. The component functions f n: P → X n have the property that 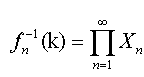 , Where
, Where
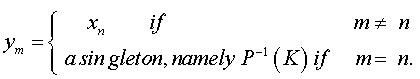
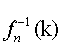 is a basic open set in the product space P, for each k in Xn. Therefore each fn is continuous. Therefore f is continuous. But f does not have a periodic point. This is because if x ∈ P and n ∈ N, then x and f”(x) necessarily differ in the n+1th coordinate.
is a basic open set in the product space P, for each k in Xn. Therefore each fn is continuous. Therefore f is continuous. But f does not have a periodic point. This is because if x ∈ P and n ∈ N, then x and f”(x) necessarily differ in the n+1th coordinate.
In fact 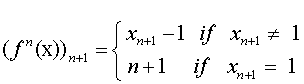
(d). The map f (x) = x+1 for all x in R, is continuous self-map of R without any periodic point.
(e). Let f: β N → β N be the unique continuous extension of the map f: N → N defined by f ( x ) = x + 1 for all x in N. We claim that f has no periodic points. If n is in N. Their closures in β N should be pairwise disjoint. If x is in β N, then x belongs to Ar, for a unique r. But f m ( Ar ) = As is disjoint from Ar if m < n. Then f m (x ) ∈ As, and hence f m (x ) ≠ x. Since n in N is arbitrary, this means that x in β N can be a periodic point of f.
Theorem 1: The following are equivalent for a metric space X.
1. X is countable and compact.
2. X is Zero-dimensional has p.p.p.
3. Every closed subspace of X has p.p.p and
4. Every continuous image of X has p.p.p.
Proof:
Step 1: It will be first proved that every countable compact Hausdorff space X has p.p.p.
Let f: X → X be continuous. Call a subset A of X as f -invariant if f (A) ⊂ A. By Zorn’s lemma, there is a minimal non-empty closed f-invariant subset A of X. Because of minimality, A has the property that for each x in A, 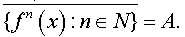
Applying Bair Category theorem to the countable compact Hausdorff space A, we obtain an isolated point a ∈ A. 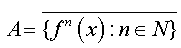 This a is in and therefore a∈{ f n (x) : n∈ N} , because a is isolated in A. This implies that a is a periodic point of f (in fact this proves that A is finite set).
This a is in and therefore a∈{ f n (x) : n∈ N} , because a is isolated in A. This implies that a is a periodic point of f (in fact this proves that A is finite set).
Step 2: Whenever X a countable compact space, so is every closed subspace of X, and so is every continuous image of X. Therefore it is immediate from step-1 that (1) implies both (3) and (4).
Step 3: It is well-known that every countable  (i.e., completely regular, Hausdorff) space X is zero-dimensional. Indeed, if x ∈ X and F is a closed subset of X not containing x, then there is a continuous function f: X → [0,1] such that f (x) = 1 and f (y) = 0 for all y in F. The rang e of this f has to be countable, since its domain is so. Therefore there is t with 0< t <1, that is not in the range of f. Now the set f −1 ([0,t )) = f −1 ([0,t]) is both open and closed in X, containing x, and disjoint from F. Similar proof can be given to show that every countable T4 space has the property that every two disjoint closed subsets can be separated by disjoint clopen sets. In particular every countable compact Hausdorff space is zero-dimensional. This observation together with step-1 proves that (1) implies (2). Thus so far we have proved that (1) implies each of the other three.
(i.e., completely regular, Hausdorff) space X is zero-dimensional. Indeed, if x ∈ X and F is a closed subset of X not containing x, then there is a continuous function f: X → [0,1] such that f (x) = 1 and f (y) = 0 for all y in F. The rang e of this f has to be countable, since its domain is so. Therefore there is t with 0< t <1, that is not in the range of f. Now the set f −1 ([0,t )) = f −1 ([0,t]) is both open and closed in X, containing x, and disjoint from F. Similar proof can be given to show that every countable T4 space has the property that every two disjoint closed subsets can be separated by disjoint clopen sets. In particular every countable compact Hausdorff space is zero-dimensional. This observation together with step-1 proves that (1) implies (2). Thus so far we have proved that (1) implies each of the other three.
Step 4: It will now be proved that every zero-dimensional metric space X with p.p.p. has no be compact. To prove this, let A = {x1, x2,……, xn…} be any countably infinite subset of X ; we shall prove that A has a limit point, If it does not, then A is discrete closed subsets of X. For each n ∈ N we choose a clopen set Vn such that (i). These are pairwise disjoint (ii). Vn ∩ A = {xn} and (iii) V ⊂ B x n . Let V0 be the complement of 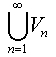 .
.
If x ∈ V0, let r>0 be such that B (x, r) ∩ A is empty. Then B(x,r / 2) ∩ Vn is empty for all n such that 1/ n < r / 2. Therefore x is not in the closure of 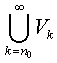 for a suitable n0.
for a suitable n0.
Nor is x in the closure of the clopen set 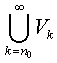 Therefore the set
Therefore the set 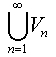 obliviously open also. Thus {V0, V1,V2,..........Vn,....} is partition of X into clopen subsets.
obliviously open also. Thus {V0, V1,V2,..........Vn,....} is partition of X into clopen subsets.
Define f: X → X by the rule f (x) = xn+1 if x ∈ Vn. Then it is easily seen that f is a continuous self-map of X without any periodic point. But X has p.p.p. by assumption. Therefore A should have a limit point. Thus X is compact.
Step 5: It will be further proved that every uncountable zero-dimensional compact metric space fails to satisfy p.p.p. Let X be one such space. For the subset S = { x ∈ X / x) admits a countable neighbourhood } the family {Vx: Vx is a countable neighbourhood of x in S} is an open cover. Because S is second countable, there should be a countable sub cover for this open cover. This implies that S is countable. Let Y be the complement of S in X. Then Y is an uncountable, zero-dimensional compact metric in which every point is a limit point. By a classical theorem [16] Y is compact that from (2) implies (1). Now it satisfy (3); every closed subspace of X has p.p.p. Then first X has to be compact, because otherwise, the infinite discrete space N is homeomorphic to some closed subset, that does not have p.p.p.by proposition 2(a).
Next, X has to be countable also, since otherwise, by a known classical result [16], X will contain a closed set homeomorphic to the Cantor set K, that does not have p.p.p. by proposition 2(c).These together prove that (3) implies (1). homeomorphic to the Cantor set K. Therefore Y admits a base {W1, W2,.....,.... Wn} of non-empty clopen (in Y) subsets such that Y = W1 ∪ W2 and Wn = W2n+1 ∪ W2n+2 for all n ∈ N. (It needs 2 W only to be noted that the standard base for the topology of the Cantor set K has this property). Moreover every infinite subfamily of this base has at most one element in the intersection. Now the sets W1 and W2 are disjoint compact subsets of the zero-dimensional Hausdorff space Y, and therefore can be separated by some clopen subsets W1 and W2 of X whose union is X. Similarly for each n ∈ N, the disjoint compact subsets W2n+1 and W2n+2 of the previously defined zerodimensional Hausdorff space Wn can be separated by disjoint clopen (in Wn and therefore in X) subsets W2n+1 and W2n+2 whose union is Wn. Thus we recursively arrive finally at a family {Wn: n ∈ N} of clopen subsets of X such that Wn ∩ Y = Wn for each n.
This family will be used to define a function r. X → Y by the rule r(x) is the unique element in Y of ∩ {Wn: n ∈ N, x ∈ Wn}.To show that this intersection set is a singleton, we first note that 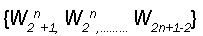 is a partition of X into clopen sets, for each n ∈ N Therefore x must belong to one and only one of these sets. In particular [17], for every m ∈ N, ∃ n>m such that x ∈ Wn.
is a partition of X into clopen sets, for each n ∈ N Therefore x must belong to one and only one of these sets. In particular [17], for every m ∈ N, ∃ n>m such that x ∈ Wn.
There are therefore infinitely many n ∈ N such that x ∈ Wn. Therefore the intersection of the corresponding Wn 's cannot have more than one element. On the other hand any such Wn's being comparable, this family has finite intersection property, and hence by compactness of X, has nonempty intersection. Thus r( x ) gets defined uniquely for each x∈ X. It is also easily seen that
(a). if x ∈ Y, then x∈ Wn ⇔ x∈ Wn. Therefore r(x) = x for x in Y.
(b). r' (Wn ) = Wn for all n. Sine {Wn: n ∈ N} is a base for Y this implies that r is continuous.
Thus r.X → Y is a retraction map. Now from proposition 1.2 (c), there is continuous self-map f:Y → Y without periodic points. Then f.r.X → Y, regarded as a map from X to X, has no periodic points at all. Thus X does not have p.p.p.
Step 6: Combining step 4 and step 5 it can be seen that (2) implies (1). Now let X countable. Next, it will be examined if this proposition is valid for all subsets of R without assuming compactness, with the help of the following proposition.
Proposition 7: Every subset of R with p.p.p. is compact.
Proof:
Let X be a subset of R with p.p.p. Then X is not the whole R by Proposition-2 (d) and cannot be an open ray, for a similar reason. If X contains an unbounded connected set, then some closed ray becomes a retract of X. This is not possible, by Remark -3. Thus
Step 7: Lastly, we prove that (4) implies (2). Let X be a metric space every continuous image of which has p.p.p. We consider two cases.
Case 1: Suppose there is some x in X and some α > 0 in R such that for β in [0,α ], there is y in X such that d (x0,y) = β.Then the function f: X → S1 defined by f (x) = exp( i..2Π/α.d (x0 , X)) is continuous and subjective. Thus S1 becomes a continuous image of X. But by proposition 2(b), S1 does not have p.p.p. Therefore this case cannot arise. This only possibility is the next case.
Case 2: For every x in X and for every α > 0 in R, there exists β in the open interval (0, α) such that α is not of the form d (x, y) for y in X. Then the open ball 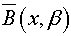 , is also the closed ball B (x, β), and is therefore a clopen set inside B (x, α). Thus X is zero-dimensional.
, is also the closed ball B (x, β), and is therefore a clopen set inside B (x, α). Thus X is zero-dimensional.
Remarks: Using these ideas, the following additional results can be proved:
1. Each of the four statements of Theorem -1 is equivalent to each of these:
(a). Neither N nor K is homeomorphic to a closed subspace of X.
(b). X is Zero–dimensional and neither N nor K is a continuous image of X.
2. A compact space X is scattered if and only if every continuous image X has p.p.p. The result of Ruddin (1957) is used.
3. Every retract of every space with p.p.p. again has p.p.p. This remark will be frequently used in what follows.
Before going to determine the subsets of R with p.p.p., it may be first observed that:
Proposition 3: Let X ⊂ R be a compact set such that X / (int X) is countable. (Here interior is taken in R ). Then X has p.p.p.
Proof: Let f: X → X be continuous function. Let X be the set of all connected components of X, provided with quotient topology from X. Sine f should map every connected component of X it induces a map f: X → X. We can easily prove that is X a countable compact metric space and that f is continuous map. Therefore by
Theorem-1, f has periodic point. Let x in X and n in N be such that fn (x) = x
Then x is a connected component [a,b] in X and fn ([a,b]) ⊂ [a,b].
It follows from the fixed point property of [a,b] that there is some x in [a,b] such that fn (x ) = x.
Thus f has a periodic point. Thus we have proved that any compact subset of R with countable boundary has p.p.p. In the next section we deal with compact subsets of R with uncountable boundary.
Proposition 4: Let X, Y be two closed subsets of R such that Y ⊂ X. Then the following are equivalent: (1). Y is retract of X and (2). a, b ∈ Y and [ a,b] ⊂ X implies that [ a,b] ⊂ Y.
Proof: (1) ⇒ (2): r. X → Y be a retraction. Assume that a and b are elements of Y and let [a, b] ⊂ X. Then r (a) = a and r (b) = b. Also r ([a,b]) should be a connected set containing r (a) and r (b). Therefore it contains [a, b ] ⊂ Y.
(2) ⇒ (1): Let (2) hold. Then no bounded component of R\Y is connected in X. Choose some xn in each bounded component (an, bn) of R\Y such that xn ∉ X.
Now define 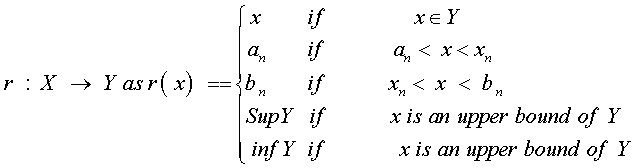
This r is continuous. Hence Y is a retract of X.
Corollary 1: Let X be a closed subset of R with empty interior. Then every closed subset of X.
Corollary 2: Let X be zero–dimensional metric space. Then every closed subset of X is a retract of X. (Since S is homeomorphic to a subspace of R).
Corollary 3: A compact metric space X is zero dimensional if and only if every closed subset of X is retract of X.
Proposition 5: Let X be a compact subset of R such that its boundary ∂X in R is uncountable. Then X does not have p.p.p [18-20].
Proof: X can have only countably many nontrivial connected components. Because, any collection of pairwise disjoint interval in R is countable. Let Y = {x ∈ X /{x} is a connected components in X}. Then by the above observation, Y = ∂X \ a countable set. Therefore by our assumption, Y is countable. By a classical theorem, every uncountable separable metric space contains a homeomorphic copy K of the Cantor set. Also Y is zero–dimensional and therefore by the above Corollary -2. x is a retract of Y.
It follows from Proposition-4 that this K is retract of X also.
Therefore by Proposition-2(c ) and Remark-3 it follows that X does not have p.p.p.
Combining Propositions 5 and 3, we have:
Proposition 6: A compact subset of R has p.p.p. if and only if its boundary is all connected components of X are bounded. If X is bounded, then X admits an infinite subset A, no two elements of which are in the same component. And A can be chosen to be the set of a sequence diverging to ∞ or −∞. Then A is a retract of X by Proposition-4, not having p.p.p.by Proposition -1 and so X is bounded.
Every connected component of X is a retract of X (by Prospostion-4), therefore having p.p.p. (by Remark-3) and is therefore either a compact interval or singleton, since other intervals do not have p.p.p. Now if x, whose terms belong to different components of X. The set A of this sequence is a retract of X is closed in R. Combining the above two proposition, the following can be obtained.
Theorem 2: A subset of R has p.p.p. if it is a compact set with countable set with countable boundary.