International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Stability Analysis of Two Dimensional Continuous Filters

Sreekala K.
Professor, Dept. of EEE, Sreenarayana Gurukulam College of Engineering, Kadayiruppu, Kerala, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

The objective of this paper is to formulate an algebraic criterion to analyze stability of two dimensional continuous filters arises in testing a driving point impedance reliability condition in power transmission lines and lumped reactance. Here the stability can be analyzed with the help of complex polynomials. In the proposed scheme which is termed as Sign Pair Criterion (SPC ), Routh-like array is developed and the elements in the first column are utilized to get the stability results. The Routh multiplication rule is applied to find all the elements of the array. This criterion is very convenient and simple compared to other available algebraic procedures for stability analysis.

Keywords
Complex polynomials, Filters, Sign pair criterion, Stability analysis, Two dimensional systems

INTRODUCTION
Stability analysis of two-dimensional linear time-invariant continuous filters arises in testing a driving point impedance reliability condition in power transmission lines and lumped reactances as discussed in [1].The polynomials in two complex variables occur in continuous systems containing both lumped and distributed elements. The bounded input bounded output stability criteria for two dimensional systems using the state-space model is explained by Wu- Sheng [2]. The analysis of stability can be carried out by the knowledge of root distribution of the characteristic equation in the case of a linear invariant continuous system
To analyse the stability of complex polynomials the generalized Routh-Hurwitz method was investigated in [3] - [7]. Frank [3] and Agashe [4] developed a new Routh like algorithm to determine the number of RHP roots in the complex case. Benidir and Picinbono [5] proposed an extended Routh table which considers singular cases of vanishing leading array element. By adding intermediate rows in the Routh array, Shyan and Jason [6] developed a tabular column ,which is also a complicated one. Adel [7] has done the stability analysis of complex polynomials using the J-fraction expansion , Hurwitz Matrix determinant and also generalized Routh’s Array.
In the case of two-dimensional continuous and discrete systems, the complex coefficients exist in the respective transformed characteristic equation as presented in [8]-[12].In these situations, to analyze stability, the direct application of Routh stability criterion is not possible. The difference between the stability theorems for the two dimensional discrete filters and those for the two dimensional continuous filters was pointed out by many authors [13]- [15]. The stability theorems for the two-dimensional continuous filters break down when the leading coefficients becomes zero, unlike the stability theorems for the two-dimensional discrete filters. Ahn [16] describes the reason why the stability theorems for the two-dimensional continuous filters encounter difficulties when the leading coefficient becomes zero in terms of the Hermite criterion. The Hermite criterion has the same difficulty even in the one dimensional filters. The Schur-Cohn criterion does not have this difficulty in the one-dimensional filters. And the stability theorems for the two-dimensional discrete filters do not suffer when the leading coefficient becomes zero. Here the Routh’s stability criterion is extended to find the stability of two dimensional continuous filters.

II. CONDITION FOR STABILITY
According to Ansell [17] a non-zero real function of two complex variables has two variable reactance property if and only if the necessary and sufficient conditions are satisfied. Consider the characteristic equation given below.
The necessary conditions for stability are as follows.
i) Coefficients of c(s1, 1) must be positive.
ii) Roots of c(s1, 1) must have negative real parts.
iii) Coefficients of c(jw, s2) must be positive.
The sufficient condition for stability is that the roots of c(jw, s2) must have negative real part and it can be checked by the proposed Sign pair criterion.

III. PROPOSED METHOD- SIGN PAIR CRITERION
For stability, the real parts of all the roots of the characteristic equation must lie on the left half of ‘s’ plane. If all the coefficients are real, Routh-Hurwitz stability test is directly applicable . In the Routh’s table, all the elements in the first column computed using Routh’s algorithm should have same sign for stability. If the coefficients are complex numbers, ‘Sign Pair Criterion is formulated as given below. In this approach, the elements of first column of Routh-like array are used to formulate the stability criterion.The characteristic equation with complex coefficients can be written as shown below.
image(2)
The first two rows of Routh-like array are written by entering the alternate real and imaginary terms of the complex coefficients. Applying the standard Routh multiplication rule, the subsequent elements of Routh-like table are computed and the table is as shown .
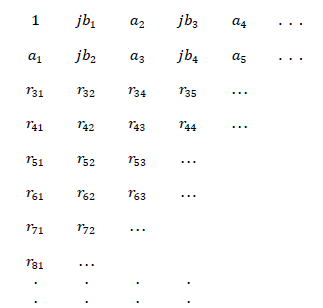image
Using the first column elements, sign pairs are formed as
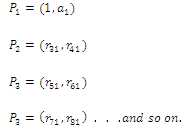image
Sign pair criterion can be stated as follows; For an nth order characteristic equation there are 2n pairs in the Routh –like table and each pair carries pure real or pure imaginary terms with same sign when the system is stable. Any violation for this condition indicates unstable situation. If the two elements in any of the pair do not possess same sign ,the system is unstable. It is ascertained that each element of the pair has to maintain the same sign for the roots of characteristic equation to lie on the left of s-plane.

IV. RESULTS
A. Example 1.
image
image

V. CONCLUSION AND FUTURE WORK
An algebraic criterion is proposed to analyze stability of two dimensional continuous filters. Here the stability can be analyzed with the help of complex polynomials. In the proposed scheme which is termed as Sign Pair Criterion (SPC ), Routh-like array is developed and the elements in the first column are utilized to get the stability results. The Routh multiplication rule is applied to find all the elements of the array. This criterion is very convenient and simple compared to other available algebraic procedures for stability analysis.

References
  1. E.I. Jury, ‘Inners and stability of dynamic systems’, Wiley Inderscience, New York ,1974
  2. L.Wu-Sheng and E.B. Lee, ,’Stability analysis for two-dimensional systems’, IEEE Transactions on Circuits and Systems, vol.30, Issue 7, pp.125-128,1983.
  3. E E. Frank , ‘On the zeros of polynomials with complex coefficients’, Bull.Amer.Math.Soc, pp. 144 – 158,1946.
  4. S.D.Agashe , ‘A new general Routh like Algorithm to determine the number of R H P Roots of a a real or complex polynomial’, IEEE Transactions on automatic control , pp.406- 409,1985.
  5. M.Benidt and B.Picinbon, ‘The extended Routh’s table in the complex case’, IEEE Transactions on Automatic Control, pp. 253-256,1991.
  6. Shyan S.Chen and Jason S.H.Tsai, ‘A new Tabular form for determining root distribution of a complex polynomial with respect to the imaginary axis’. IEEE Transactions on Automatic Control, pp.1536-1541, 1993
  7. A.M.K .Hashem, ‘Network Synthesis of Complex Impedance and Complex Reactance Functions ‘,Ph.D Thesis, Concordia University, 1993.
  8. Ohannessian, MI, Kabalan, KY and El-Haji A , ‘Complex coefficient polynomial roots by a stability criterion’, International Journal of Information and Systems Sciences, vol.1, Issue 1, pp.89-104,2005.
  9. Verriest, EI and Michiels, W , ‘Routh–Hurwitz criterion and stabilility of neutral systems’, Proceedings of the 42nd IEEE Conferences on Decision and control, USA, pp. 5060- 5065,2003.
  10. Chen, SS and Tsai JSH ,‘A new tabular form for determining root distribution of a complex polynomial with respect to the imaginary axis’, IEEE Transactions on Automatic Control, vol.38, Issue 10, pp.1536-1541, 1993.
  11. Shi, YQ ,Yen, KK and Chen, CM , ‘Two necessary conditions for a complex polynomial to be strictly Hurwitz and their application in robust stability analysis’, IEEE Transactions on Automatic Control, vol.38, Issue 1, pp.125-128, 1993.
  12. Sondergeld, KP , ‘A Generalization of the Routh – Hurwitz stability criteria and an application to a problem in robust controller design’, IEEE Transactions on Automatic Control, vol.28, Issue 10, pp. 965 -970, 1983.
  13. J. P. Guiver and N. K. Bose, ‘On test for zero-sets of multivariate polynomials in non compact poly domains’, Proc. IEEE ,vol. 69, pp. 467-469, 1981.
  14. E. I. Jury, ‘Stability of multidimenslonal scalar and matrix polynomials,’ Proc. IEEE, vol. 66, pp. 1018-1047, 1978.
  15. P. K. Rajan, H. C. Reddy, M. N. S. Swamy. and V. Ramachandran, ‘Generation of two-dimensional digital functions without nonessential singularities of the second kind,’ IEEE Trans. Acoust., Speech, Signal Process., vol. ASSP-28, pp. 216-223, 1980.
  16. S.M. Ahn, ‘On the stability of Two Dimensional Continuous Filters’, Proc. IEEE ,vol. 73, Issue 11,pp. 467-469, 1985.
  17. Ansell, HG , ‘On certain two-variable generalizations of circuit theory, with applications to networks of transmission lines and lumped reactances’, IEEE Transactions on Circuit Theory, vol.11, Issue 2, pp.214-223, 1964.
  18. Bose, NK , ‘Implementation of a new stability test for two-dimensional filters’, IEEE Transactions on ASSP, vol.25, Issue 2, pp.117-120, 1977.