Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

State Estimation by Discrete Reduced Order UI Observer and Discrete Kalman Filter for Linear Systems

M.S. Das1, S. K. Singh2
  1. Assistant Professor, Department of ECE, NSHM Knowledge Campus, Durgapur, West Bengal, India
  2. Assistant Professor, Department of ECE, NSHM Knowledge Campus, Durgapur, West Bengal, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

In this paper unknown input observer using projection operator method is used to estimate five states of the fifth order lateral axis model of L-1011 system in discrete domain. Discrete reduced order UI observer is used to estimate the states of the system in noiseless and noisy environment. Kalman filter has been designed to estimate the state of L-1011 system when noise is considered. Finally error between the actual and estimated states of the system by UI observer and Kalman filter i.e performance of both are compared. It has been shown that Kalman filter is good estimator than UI observer in noisy environment in respect of estimation. The simulations have been done using MATLAB and SIMULINK Toolbox & the results of the simulations have been displayed in this paper.

Keywords
Unknown input observer (UIO), projection operator method, Estimated state, Estimated error, Kalman filter.

INTRODUCTION
Observer and Kalman filter is widely used in estimation of different linear and non linear systems. Many authors have designed unknown input observer in different approach and Kalman filter for estimation of linear and non linear systems. Over the past three decades, many significant works have been carried out on the construction of observers for linear and nonlinear systems in the control systems literature[1-15].The observer was first proposed and developed by Luenberger in the early sixties of the last century [1][2][4].Full order and reduced order observer was introduced to estimate the states of the linear and non linear systems[12][16].Sliding mode observer were proposed for uncertain systems[7][13][14]. Later, Sliding mode observer was introduced for fault detection and isolation [14-15]. Observers for systems with unknown inputs has an important role in robust model-based fault detection [14][15].Alexander Stotsky and Ilya Kolmanovsky designed an observer to estimate the unknown input from available state measurements in automotive control application [18]. Talel. Bessaoudi, Karim Khemiri, Faycal. Ben Hmida and Moncef. Gossa [19] estimate the unknown input and states of a linear discrete time systems using recursive least-square approach.Estimation of states and unknown input of a nonlinear communication system has been addressed [20].Kalyana C. Veluvolu and Soh Yeng Chai designed a high gain observer with multiple sliding mode for state and unknown input estimations[21]. Simultaneous estimation [22] of states and unknown input for a class of nonlinear systems has been proposed by Q. P. Ha and H. Trinh. Thierry Floquet and Jean-Pierre Barbot designed a state and unknown input delayed estimator for discrete-time linear systems [23]. Abhijit Banerjee and Prof. G. Das [24] used the reduced order observer [26] to estimate the unknown input of a linear time invariant system. Ashis De, Abhijit. Banerjee and Prof. G. Das [25] estimate the unknown input of an LTI system using full order observer constructed by the method of generalized matrix inverse [27].
In 1960, R.E. Kalman published his famous paper [28] describing a recursive solution to the discrete-data linear filtering problem. Since then,the Kalman filter has been the subject of extensive research and application, particularly in the area of autonomous or assisted navigation.Many researchers are using different Kalman filter like Discrete Kalman filter Extended Kalman filter[31] ,Unscented Kalman for estimation of tracking[31-32], military system, flight control system, Image and video tracking in a real time system etc.The filter is said to be very powerful as it can estimate the state of a process even when the precise model of the system is unknown. A Kalman filter is simply an optimal recursive data processing algorithm that blends all available information, including measurement outputs, prior knowledge about the system and measuring sensors, to estimate the state variables in such a manner that the error is statistically minimized In practice, linear equation system with white Gaussian noises is commonly taken as the standard model of a Kalman filter.
Stefen Hui and Stanislaw H. Zak [17] designed both unknown input full order and reduced order observer using projection operator method in continuous domain. They did not estimate the states of the L-1101system in noisy environment. In this paper a discrete reduced order UI observer using projection operator has been designed to estimate the states of L-1011 system in noisy environment. Also discrete Kalman filter is used to estimate the states. Finally accuracy in estimation by discrete Kalman filter and observer is compared.

II. SYSTEM’S MODEL AND DESCRIPTION
image

III.DISCRETISED MODEL OF REDUCED ORDER UNKNOWN INPUT OBSERVER
At first the continuous fifth order lateral axis model of L-1101 system and reduced order unknown input observer are discretized .This discrete UI observer is used to estimate the state of discrete system ( fifth order lateral axis model of L-1011 system).Firstly it is applied on the system to estimate the state in noisy and without noisy condition. Here it has been seen that Sampling time is taken 0.01 sec during discretisation .Dynamic Model of the discretised L-1011 system and reduced order unknown input observer using projection operator is given below respectively .
X(k+1) = Ad x(k) + Bd u(k) and Y (k) = Cd x (k) + Dd u (k); Where
image

IV. SIMULATION RESULT (WITHOUT NOISE)
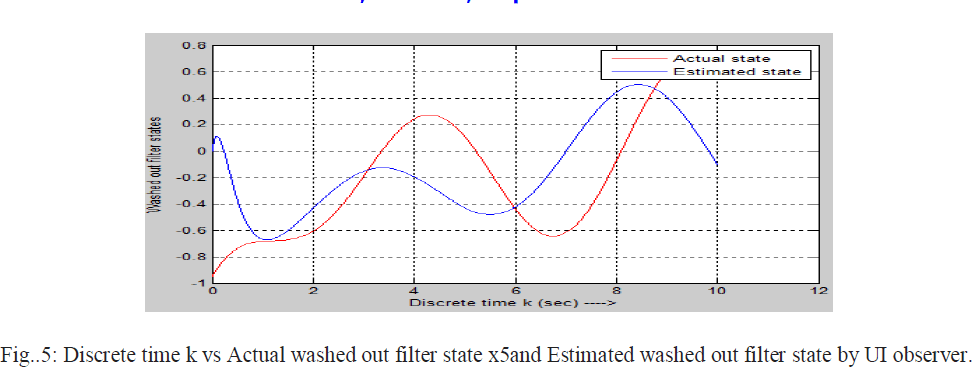
Actual state and estimated state by UI observer using projection operator method [1] and error are shown below
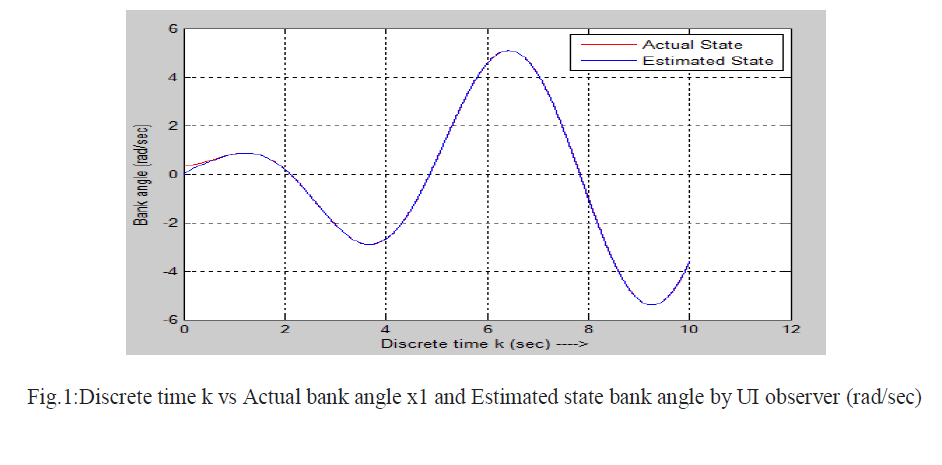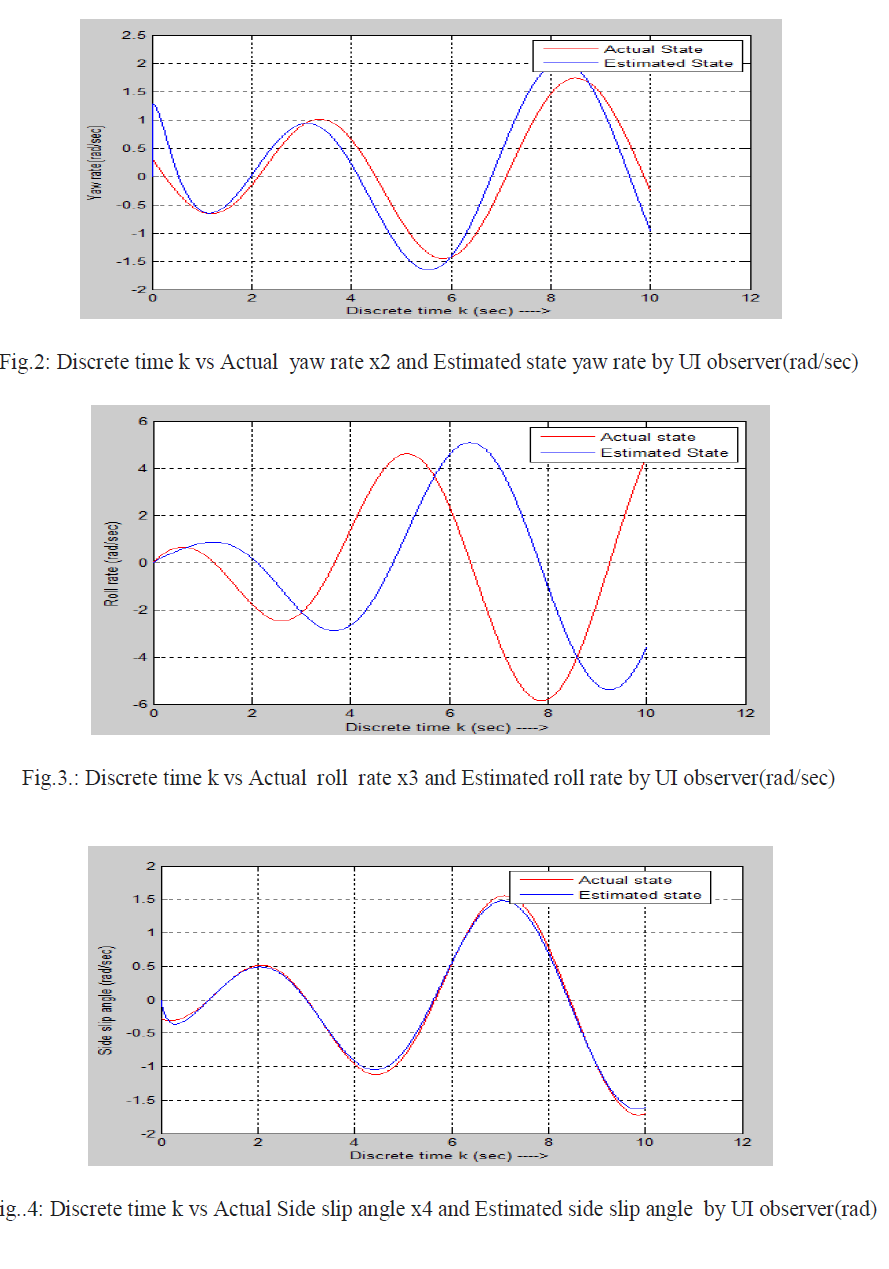image
image
image

V.ESTIMATION BY REDUCED ORDER UI OBSERVER WHEN NOISE IS INTRODUCED IN THE SYSTEM
All systems are affected by unwanted noise that changes the actual output or actual state. Here it is assumed that the noise that is introduced with the system (Fifth order lateral axis model of L-1011) is zero mean white Gaussian in nature.UIO is applied on noisy system to estimate state of the system.

VII. SIMULATION RESULT (IN NOISY ENVIRONMENT)
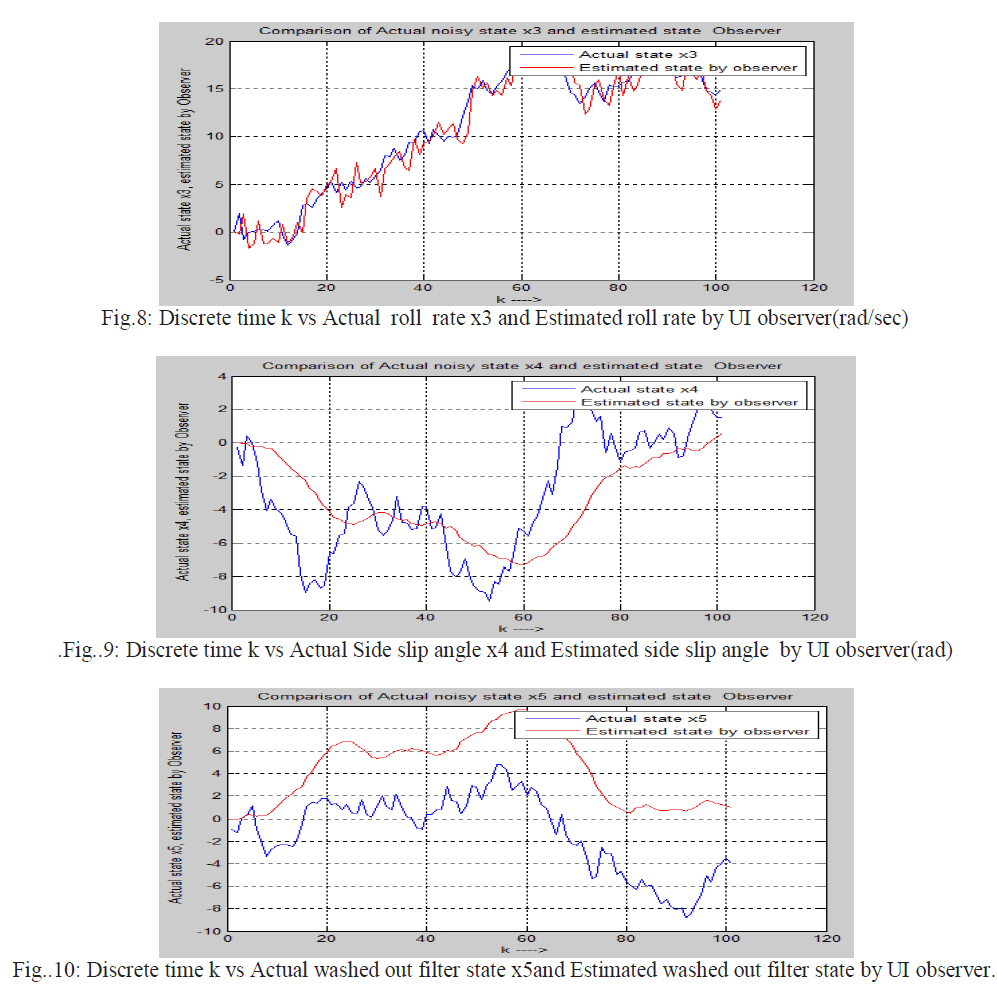
Actual state of the noisy system estimated state by reduced order observer using projection operator method in discrete domain has been shown in below
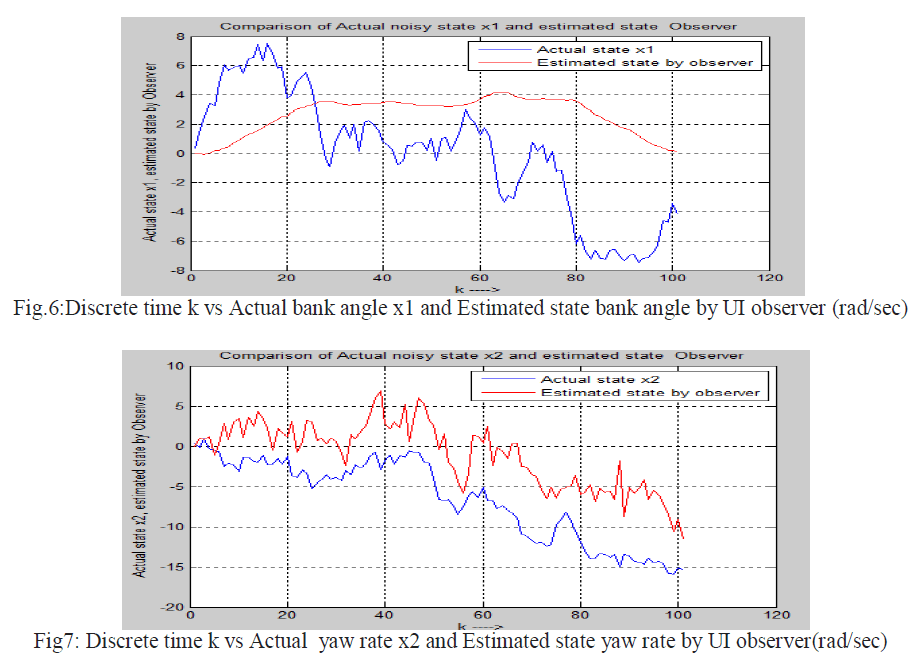image
image

VII. STATE ESTIMATION BY DISCRETE KALMAN FILTER
The Kalman filter is a mathematical method named after Rudolf E. Kalman.The Kalman filter produces estimates of the true values of measurements and their associated calculated values by predicting a value, estimating the uncertainty of the predicted value, and computing a weighted average of the predicted value and the measured value. Weight is chosen such that uncertainty is minimum. It is an essential part of development part of space and military technology. The Kalman filter is very important tool which is used to estimate the state of noisy linear dynamic system, described in state space form. It provides a recursive solution to the linear optimal filtering problem. It can be applied in stationary and non stationary environments. The solution is recursive in that each updated estimate of the state is computed from the previous estimate and the new input data, so only the previous estimate requires memory. In this case it is essential to store only the previous estimate instead of storing entire past state.Kalman filter is computationally more efficient than computing the estimate directly from the entire past observed data at each step of the filtering process.The state is the least amount of data on the past behavior of the system that is needed to predict its future behavior.Typically, the state xk is unknown. To estimate it, we use a set of observed data, denoted by the vector yk.Process equation can be written as
x(k+1)= Φ(k) x(k) + Bu(k) + wk
Where Φk is the state transition matrix of nxn dimension taking the state xk from time k to time k + 1. The process noise wk is assumed to be additive, white,and Gaussian, with zero mean wk ~ N(0,Q), Where Q process noise covarinace matrix. and with process noise covariance matrix defined by E(wn* wT k) = Qk when n=k otherwise zero. Measurement equation can be written as
Zk=Hxk+vk
where, vk is the measurement noise of m x 1 vector which is denoted by vk~N(0,R) where R measurement noise covariance matrix. xk = n×1 process state vector at time tk. zk = m × 1 measurement at time tk and C = Output matrix. Kalman Filter estimate state in two phase one is predict and another is update .Predict Equations and update equations are given below. In predict phase it uses the state estimate from the previous time step to produce an estimate of the state at the current time step.
Predicted state (a priori state) :  xˆk =A ˆk 1 x +B u k-1 And predicted(a priori state) error covariance Pk= APk-1 Á+Q
The current a priori prediction is combined with current observation information to refine the state estimate. This improved estimate is termed as posteriori state estimate. Typically, the two phases alternate, with the prediction advancing the state until the next scheduled observation and the update incorporating the observation.Updates equations are given below..
image

VIII. ESTIMATION BY KALMAN FILTER
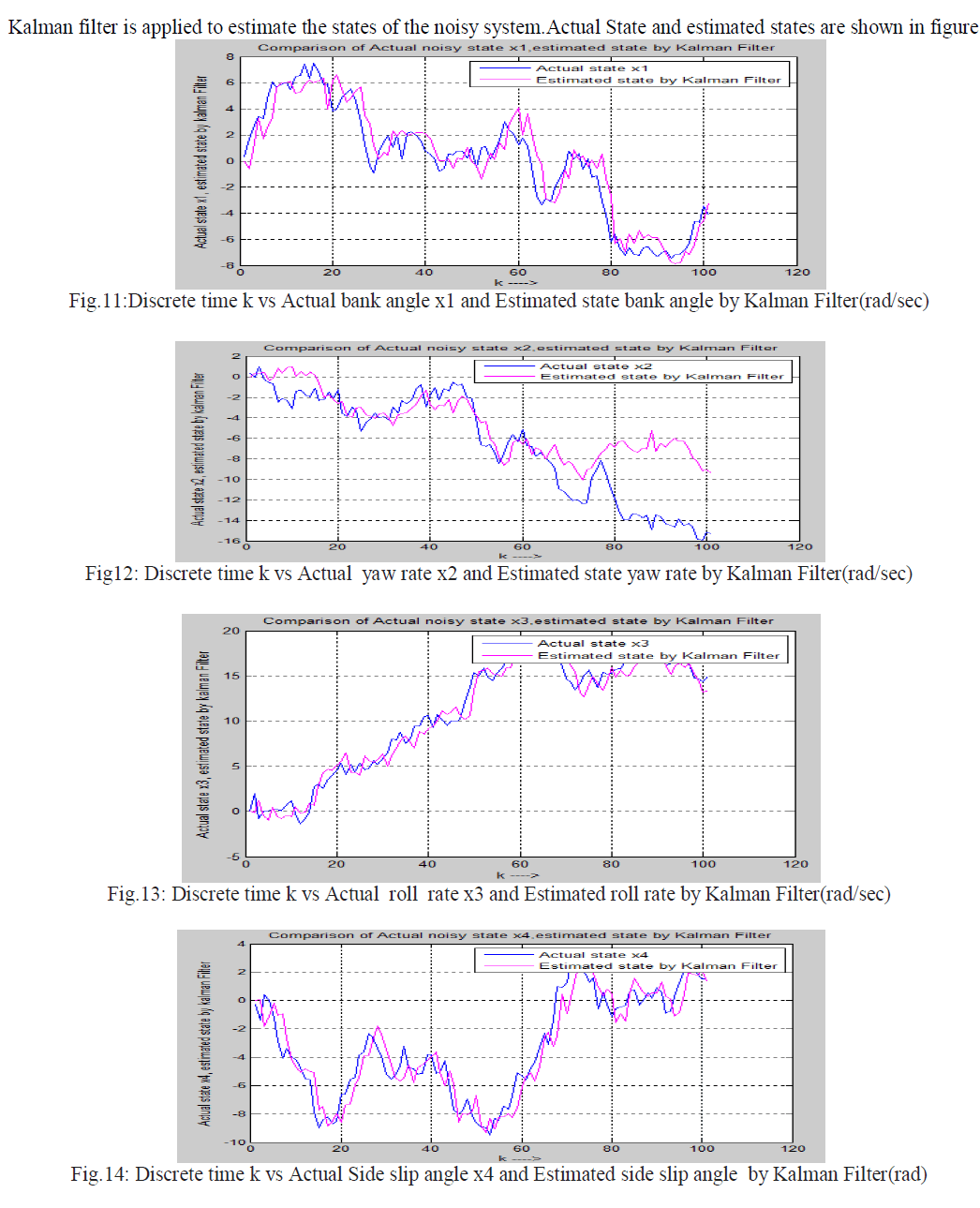
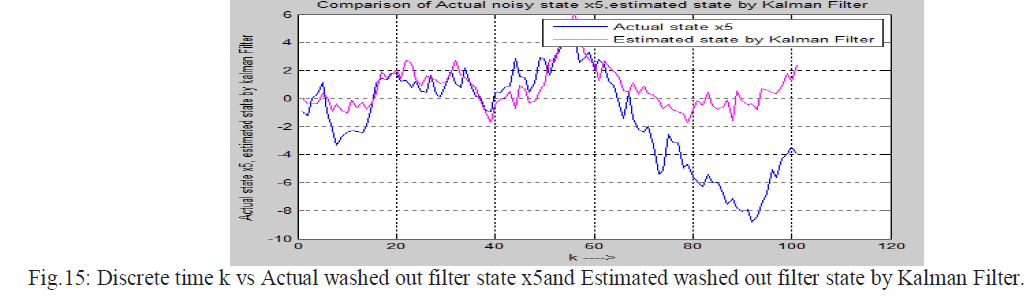
The discrete Kalman filter is applied on noisy fifth order lateral axis model o L-1011 system to estimate the state of the system. Here it is assumed zero mean white Gaussian noise is mixed with system and output equation .It means process noise Wk and measurement noise Vk all are zero mean white Gaussian noise. So process noise Wk and measurement noise Vk can be represented as Wk ~N(0,Qk) and Vk ~N(0,Rk) Where Qk is process noise covariance matrix and Rk measurement noise covariance matrix.It is assumed that process noise covariance matrix Qk and measurement noise covariance matrix Rk is identity matrix. The value of Qk and Rk is given below.
image

IX. SIMULATION RESULTS
image
image

X.COMPARISON OF ESTIMATED ERROR BETWEEN KALMAN FILTER AND UI OBSERVER (PROJECTION OPERATOR METHOD)
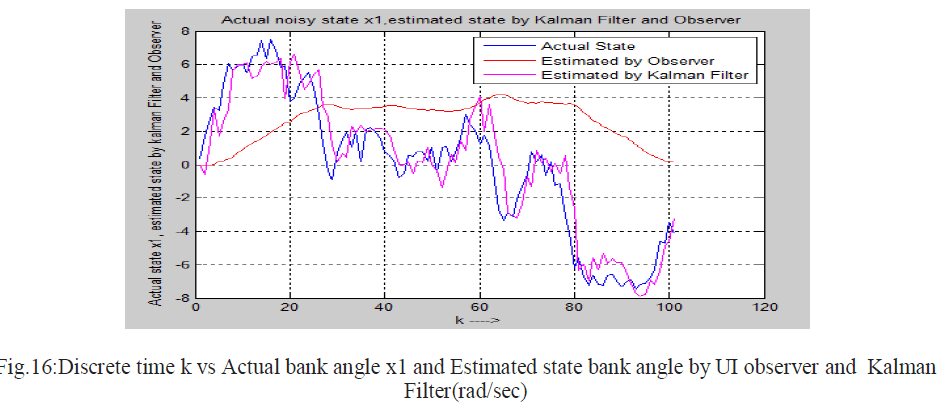
In this thesis the comparison of Kalman Filter and Unknown Input Observer is shown. These Two techniques ie discrete Kalman Filter and discretised Unknown Input Observer (using projection operator approach) are applied on a same noisy system to estimate the state of the system. These two techniques are applied on the fifth-order lateral axis model of an L-1011 fixed wing aircraft model. Here it is considered that zero mean white Gaussian noise is introduced to the system .First Unknown Input observer and secondly Kalman Filter is applied on same the noisy system to estimate the state and hence estimated error is calculated for each cases .Estimated state error by UI observer and The Kalman Filter is given below. There are five state in the system i.e five error plot is shown below. Five states are as follows x1=Φ , bank angle (rad), x2=yaw rate (rad/sec), x3=roll rate (rad/sec) , x4=sideslip-angle (rad) and x5=washed out filter state.

XI.SIMULATION RESULT
Actual state of a noisy system , estimated state by UI observer using projection operator method and estimated state by Kalman filter in noisy environment are shown in the following figure.
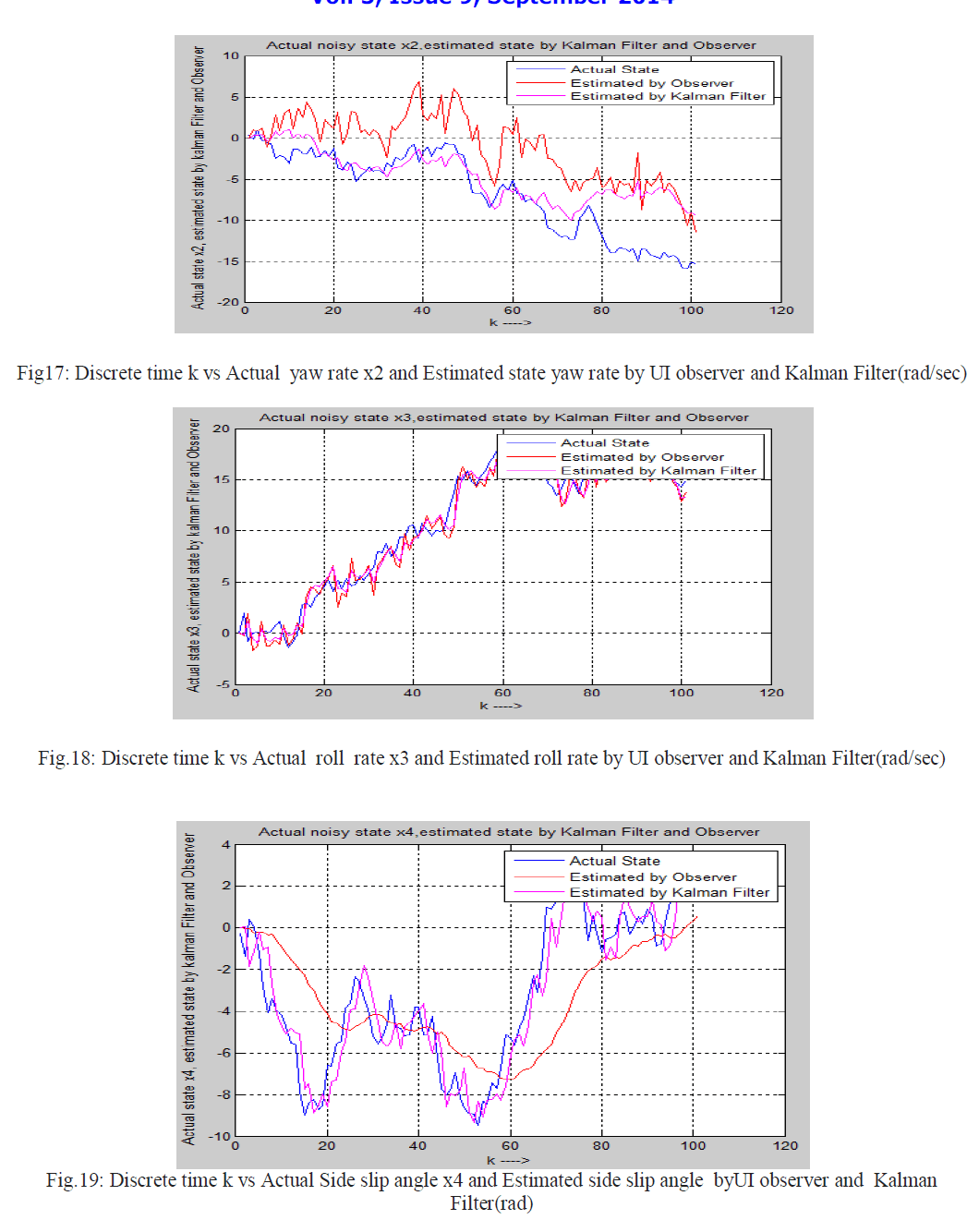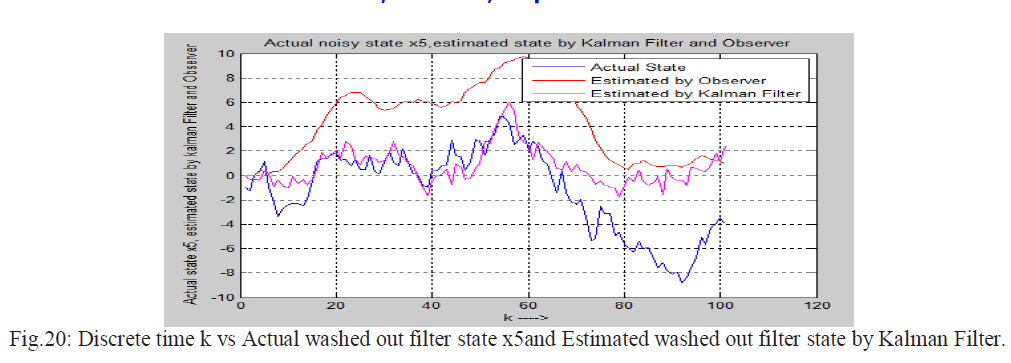image
image
image

COMPARISON OF ERROR OF KALMAN FILTER AND UI OBSERVER
Errors in estimation of states by Kalman Filter and UI reduced order observer are compared . Comparison of errors are shown in the following figure.
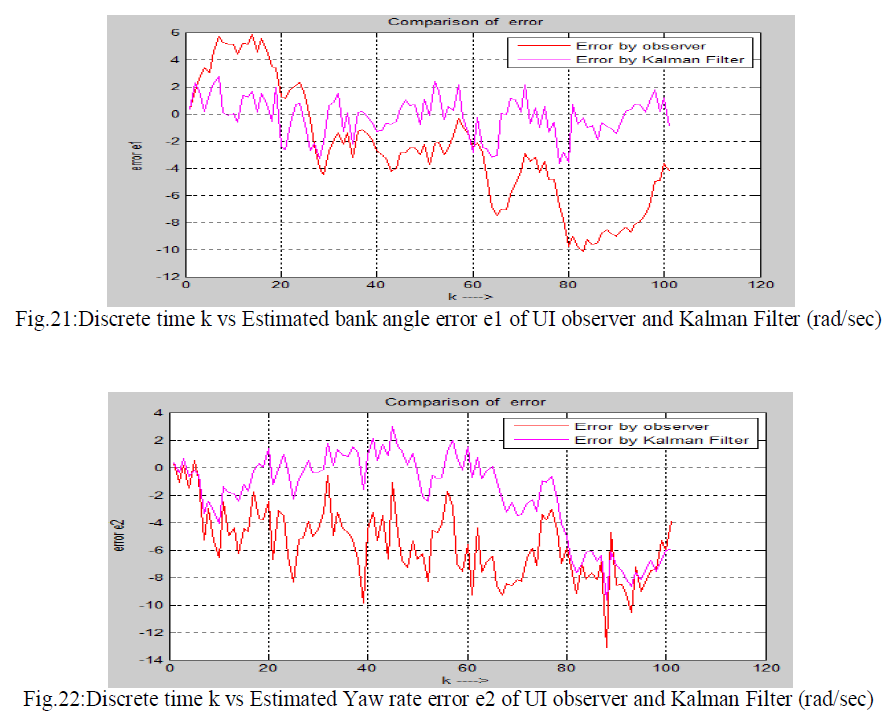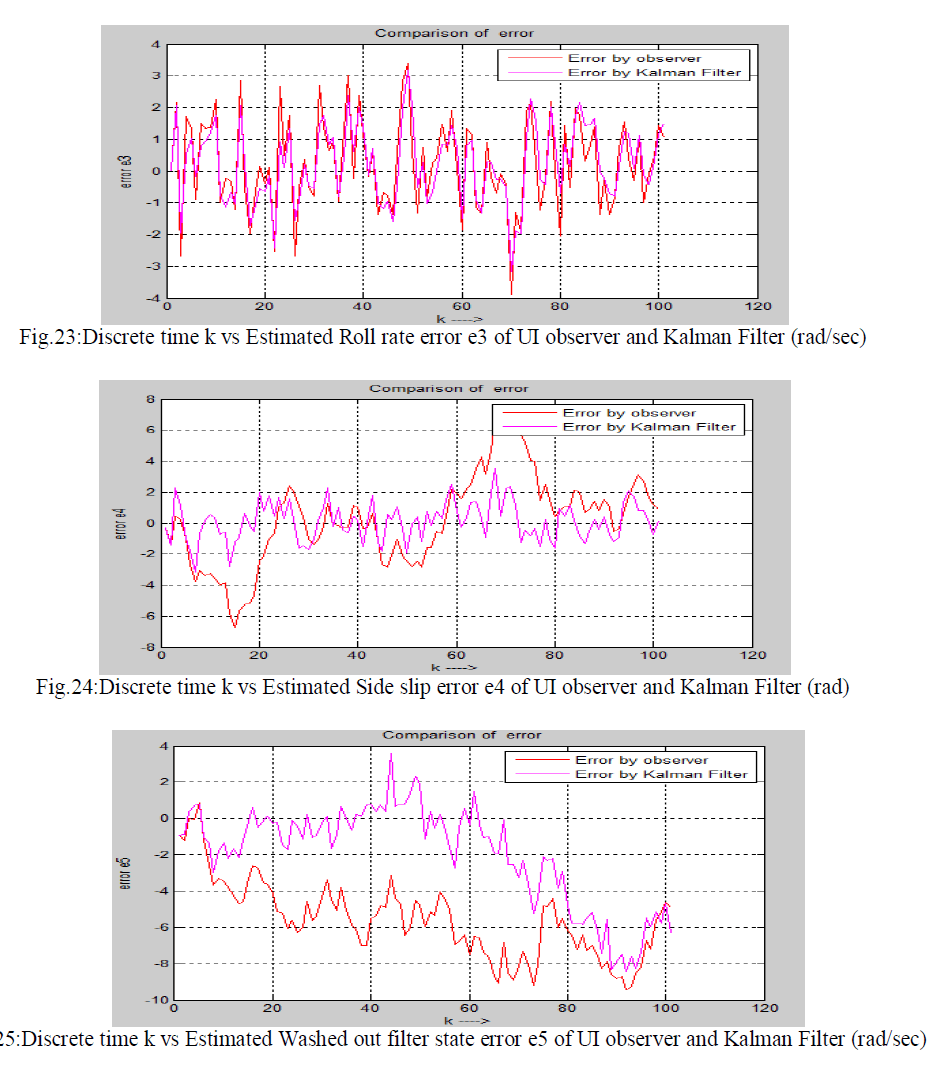image
image

RMS ERROR COMPARISON
Finally I have compared the RMS error of UI observer and RMS error of Kalman Filter and error covariance. Simulated outputs are shown in the following figures.
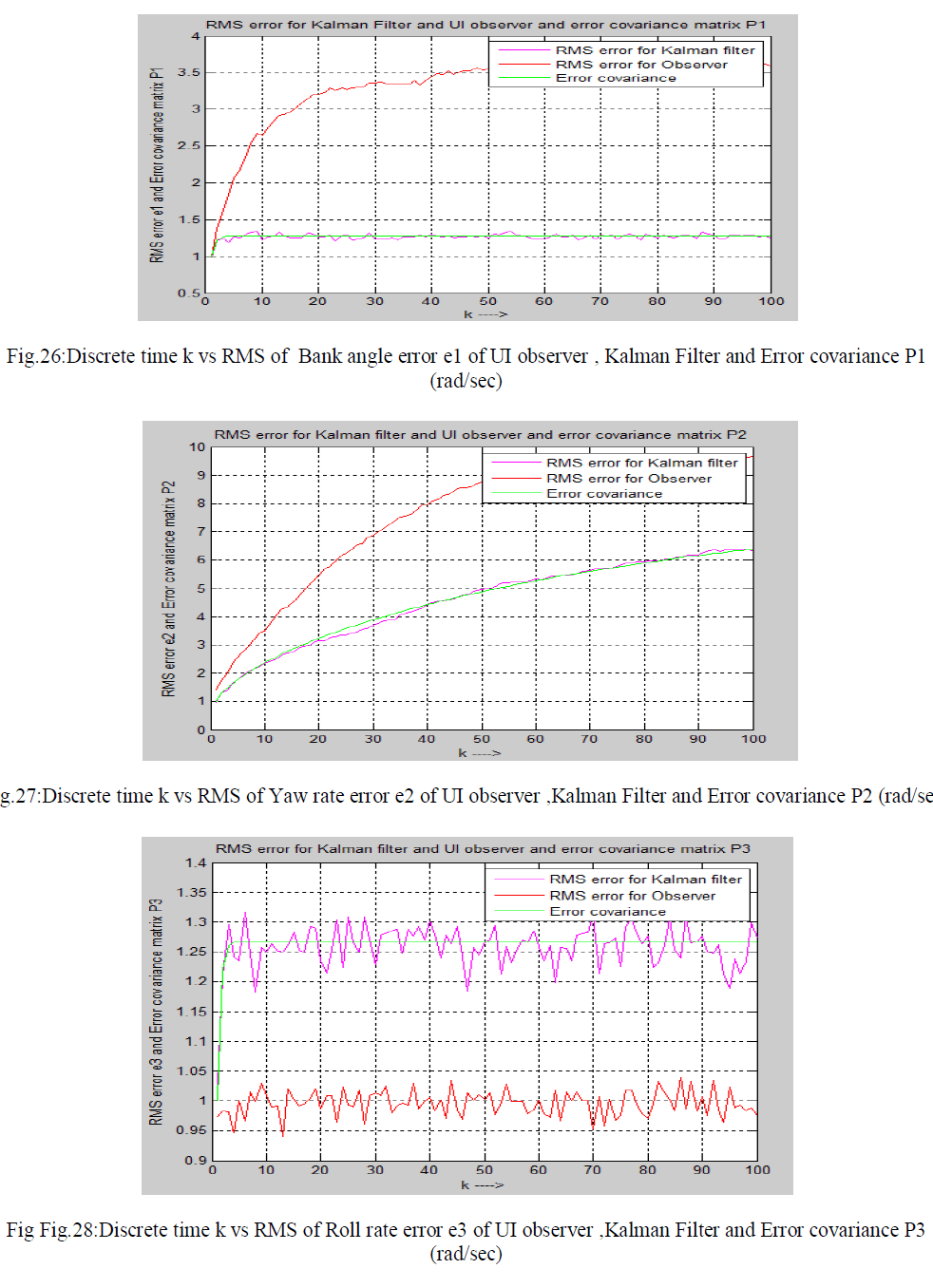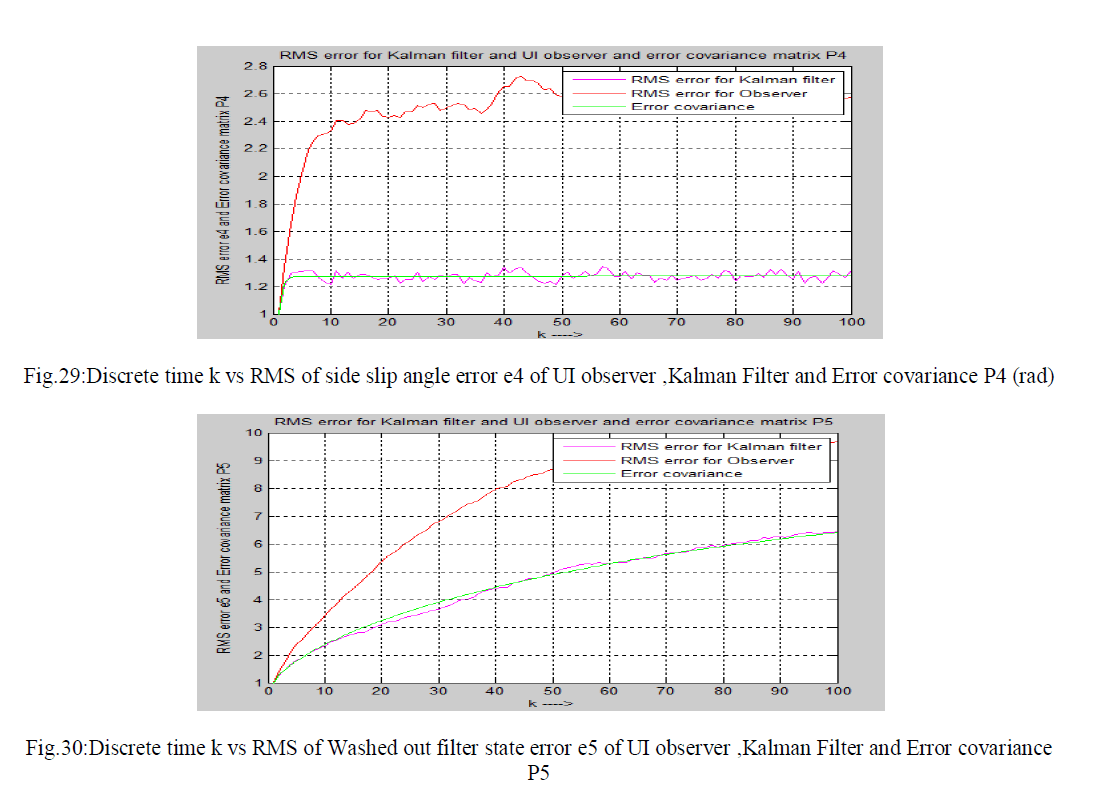image
image

XII.CONCLUSION
This paper summarizes a number of conclusions that can be drawn from the work . Reduced order unknown input observer is used here to estimate the state of the fifth order lateral axis model of an aircraft model of L-1011 in continuous and discrete domain. Also it is seen that UIO is capable of estimating state of a system in noisy environment in discrete domain. Here initial value of UIO observer q(0) is assumed to be zero.It is seen that estimated error using UIO using projection operator method is low in noise free system.It is a good estimator for noise free system. But it gives poor performance in estimation in noisy environment. Finally discrete Kalman filter is used to estimate the state of the fifth order lateral axis model of an aircraft model of L-1011 system in noisy environment. Kalman filter is good minimum variance estimator and it gives satisfactory result in noisy environment.It is easy to conclude from the error plot ( in fig. 21 to fig.25) and RMSE plot( in fig.26 to fig.30) that Kalman fillter is more efficient estimator than unknown input observer in noisy field. There is some limitation of using Kalman filter .We should know mean and correlation of the process noise Wk and measurement noise vk at each time instant.We should know process noise covariance Q , measurement noise covariance R and error covariance P also. If it is not given then estimation by Kalman filter is not possible correctly. In this paper process noise Wk and measurement noise vk is assumed to be zero mean white Gaussian noise .The value of P,Q,R is assumed as identity matrix in this paper.We have applied Kalman filter and UI observer to estimate state for the linear system only not for non-linear system. In future Extended Kalman Filter ,Unscented Kalman Filter ,UI observer ,Sliding mode observer, particle filter and Disturbance observer will be applied to estimate states of non-linear systems and compared their performance in estimation.

ACKNOWLEDGEMENT
I would like to thank to all professors of the department of Electrical Engineering, Kolkata, Jadavpur University and particularly to my guide, my Professor, Dr. Smita Sadhu . I am greatly indebted to her for his valuable advice, suggestion, kind co-operation, liberal help and guidance extended throughout the preparation of my work. It is my proud privilege to thank Professor Dr. T.K Ghoshal for encouragingto work.

References
  1. Luenberger D. G. “ Observers for multivariable systems”— IEEE Trans. Automat. Contr., Vol. AC-11, No. 2, pp. 190–197, 1966.
  2. D.G.Luenberger,“an introduction to observers”, automatic control, IEEE transaction,vol16, no. 6 , pp 596-602, Dec 1971
  3. Wang S.-H., Davison E. J. and Dorato P., “Observing the states of systems with unmeasurable disturbances”—IEEE Trans. Automat. Contr.,
  4. Vol. AC-20, No. 5, pp. 716–717,1975.
  5. Luenberger D. G, “ Introduction to Dynamic Systems:Theory, Models, and Applications” New York: Wiley,1979
  6. Bhattacharyya S. P. , “Observer design for linear systems with unknown inputs.” — IEEE Trans. Automat. Contr.,Vol. AC-23, No. 3, pp. 483– 7. 484, 1978.
  7. Yang F. and Wilde R. W. , “Observers for linear systems with unknown inputs.” — IEEE Trans. Automat. Contr.,Vol. 33, No. 7, pp. 677–681, 1988.
  8. Zak S. H. and Walcott B. L. “ State observation of nonlinear control systems via the method of Lyapunov, In: Deterministic Control of Uncertain Systems”, (A. S. I. Zinober,Ed)., London: Peter Peregrinus Ltd, Ch. 16, pp. 333–350,1990.
  9. Chen J., Patton R. J., and Zhang H.-Y. Design of unknown input observers and robust fault detection filters. ,Int. J. Contr., Vol. 63, No. 1, pp. 85– 105. ,1996.
  10. Chang S.-K., You W.-T., and Hsu P.-L. , “ Design of general structured observers for linear systems with unknown inputs” — J. Franklin Instit., Vol. 334B, No. 2, pp. 213–232,1997.
  11. Corless M. and Tu J., “ State and input estimation for a class of uncertain systems” — Automatica, Vol. 34, No. 6,pp. 757–764, Vol. 334B, No. 2, pp. 213–232.
  12. Chen J. and Patton R. J. Robust Model-Based Fault Diagnosis for Dynamic Systems. —Boston: Kluwer., 1999.
  13. Darouach M., Zasadzinski M., and Xu S. J. , “Full-order observers for linear systems with unknown inputs”,IEEE Trans. Automat. Contr., 15. Vol. 39, No. 3, pp. 606–609. 1994.
  14. Edwards C. and Spurgeon S. K. , “Sliding Mode Control:Theory and Applications.”London: Taylor and Francis,1998. 17. Edwards C., Spurgeon S. K., and Patton R. J. , “Slidingmode observers for fault detection and isolation”,Automatica, Vol. 36, No. 4, pp. 541– 553,2000.
  15. Saif M. and Xiong Y., “Sliding mode observers and their application in fault diagnosis, In: Fault Diagnosis and 19. Fault Tolerance for Mechatronic Systems”, (F. Caccavale and L. Villani, Eds.), Berlin: Springer, pp. 1–57.2003.
  16. Stefen Hui and Stanishlaw H. Zak, “Observer design for systems with unknown inputs”, Department of Mathematical Sciences San Diego State University, Int. J. Appl. Math. Comput. Sci., Vol. 15, No. 4, 431–446,2005.
  17. Xiang J., Su H., and Chu J. , “ On the design of Walcott- Zak sliding mode observer.” Proc. Amer. Contr. Conf. Portland, OR, pp. 2451– 2456,2005.
  18. Alexander Stotsky, Ilya Kolmanovsky, “Simple unknown input estimation techniques for automotive applications”, Proceedings of the American Control Conference, Arlington, VA, pp. 3312-3317, June 2001.
  19. Talel. Bessaoudi, Karim. Khémiri, Fayçal. Ben Hmida and Moncef. Gossa, “Recusive least-squares estimation for the joint input- state estimation of linear discrete time systems with unknown input” International Multi- Conference on Systems, Signals & Devices, 2011
  20. Mohamed Benallouch, Mohamed Boutayeb, Rachid Outbib and Edouard Laroche, "Nonlinear estimation of states and unknown inputs for 25. communication systems”, Proceedings of IEEE International Conference on Signal Processing and Communications (ICSPC 2007), Dubai, United Arab Emirates, pp. 696-699, 2007.
  21. Kalyana C. Veluvolu, Soh Yeng Chai. "High gain observers with multiple sliding mode for state and unknown input estimations." 4th IEEE 27. Conference on Industrial Electronics and Applications (ICIEA), pp. 1179-1186, 2009.
  22. Thierry Floquet, Jean-Pierre Barbot, “State and unknown input estimation for linear discrete-time systems”, Automatica 42(2006), pp. 1883- 1889, Sept. 2006.
  23. Avijit Banerjee, Gourhari Das, “Estimation of unknown input using reduced order Das and Ghoshal Observer”, IEEE International Conference on Emerging Trends in Computing, Communication and Nanotechnology (ICECCN 2013), pp. 394-397, 2013.
  24. Ashis De, Avijit Banerjee, Gourhari Das, “Unknown input estimation using full order observer in the domain of generalized matrix inverse”, 31. International Journal of Engineering Research and Development, vol. 8, issue 9, pp. 01-05, Sept. 2013.
  25. G. Das and T. K. Ghoshal, “Reduced-order observer construction by generalized matrix inverse”, International Journal of Control, vol. 33, no. 2, pp. 371-378, Jan. 1981.
  26. Avijit Banerjee, Gourhari Das, “Comparison between construction methods of unknown input reduced order observer using projection operator 34. approach and generalized matrix inverse”, International conference on Electrical, Electronics Engineering, Bhopal, ISBN: 978-93-82208-47-1, pp. 05-10, Dec. 2012.
  27. Avijit Banerjee, Partha Pratim Mondal, Gourhari Das, “Construction of Full order observer for linear time invariant systems using generalized matrix inverse”, Proceedings of IEEE International Conference on Information and Communication Technologies (ICT 2013), pp. 711-714, 2013.
  28. Rudolf E. Kalman, “ A new Approach to Linear Filtering and prediction problems”, Transaction of AMSE, , pp 35-45, March 1960.
  29. Brown and Hwang, “Introduction to Random Signals and applied Kalman filtering”, 2nd edition, John wiley and sons Inc.1983.
  30. Greg Welch and Gary Bishop, “ An Introduction to the Kalman Filter” ,Department of Computer Science, University of North Carolina ,Chapel Hill NC 27599-3175, July 24, 2006.
  31. Reshma A. R., S.Anooja , George Deepa Elizabeth , “Bearing Only Tracking Using Extended Kalman Filter”, International Journal of Advanced Research in Computer and Communication Engineering ,Vol. 2, Issue 2, February 2013 .
  32. Wan, E., Van Der Merwe, R., “ The unscented Kalman for nonlinear estimation” ,.In: Proceedings of Symposium.,pp.153-158,2000.